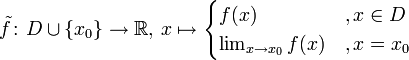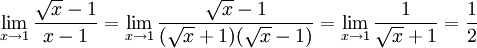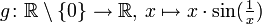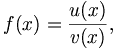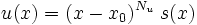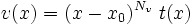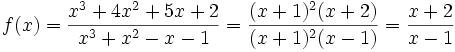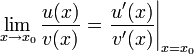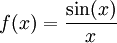- Stetige Fortsetzung
-
Die stetig behebbare oder hebbare Definitionslücke tritt unter anderem bei Funktionen der Mathematik auf, die aus der Division einer Funktion durch eine zweite entstehen.
Formal geschrieben sei
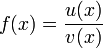 .
.
Prinzipiell können sowohl u(x) als auch v(x) den Wert Null annehmen. Man hat dann folgende drei Situationen:
- eine Nullstelle, wenn u(x) = 0 und
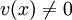 ;
; - eine Polstelle oder auch Unendlichkeitsstelle, wenn
 und v(x) = 0;
und v(x) = 0; - eine Lücke, auch als unbestimmter Ausdruck bezeichnet, wenn u(x) = v(x) = 0.
Eine Definitionslücke kann, je nach dem Verhalten der Zähler- und Nennerfunktion, eine Polstelle oder aber eine stetig ergänzbare Lücke sein (Polstellen können hingegen nicht stetig ergänzt werden).
Anmerkung: Die Ausdrücke stetig behebbar, stetig ergänzbar und stetig fortsetzbar werden gleichbedeutend verwendet. Auch der Ausdruck hebbare Definitionslücke ist geläufig. In der Funktionentheorie spricht man von einer hebbaren Singularität.
Zu beachten ist, dass f an den Stellen, bei denen der Nenner gleich 0 ist, zunächst eine Lücke im Definitionsbereich angenommen werden muss. Zur Untersuchung der stetigen Fortsetzbarkeit ist daher eine genauere Betrachtung der Umgebung notwendig! So ist z. B. die Funktion f(x) = 1 / x in ihren gesamten Definitionsbereich
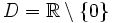 stetig, hat aber an der Stelle 0 eine Definitionslücke, die sich bei genauerer Betrachtung als eine Polstelle herausstellt.
stetig, hat aber an der Stelle 0 eine Definitionslücke, die sich bei genauerer Betrachtung als eine Polstelle herausstellt.Inhaltsverzeichnis
Definition der stetigen Fortsetzung und der stetigen Fortsetzbarkeit einer Funktion
Gegeben sei eine Funktion
 und
und 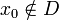 ein Häufungspunkt von D.
ein Häufungspunkt von D.Die Funktion
 heißt stetige Fortsetzung von f (auf
heißt stetige Fortsetzung von f (auf 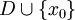 ), falls
), falls  auf D mit f übereinstimmt und
auf D mit f übereinstimmt und  in x0 stetig ist.
in x0 stetig ist.Existiert eine solche stetige Fortsetzung, so heißt f in x0 stetig fortsetzbar.
Anmerkung: Diese Definitionen lassen sich analog für komplexwertige Funktionen formulieren.
Eigenschaften
Für eine stetige Fortsetzung muss
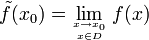 gelten, es kann also höchstens eine stetige Fortsetzung geben.
gelten, es kann also höchstens eine stetige Fortsetzung geben.Umgekehrt gilt: Falls der Grenzwert
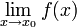 existiert (uneigentliche Grenzwerte, also
existiert (uneigentliche Grenzwerte, also 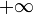 oder
oder  , liegen nicht in
, liegen nicht in 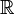 und sind hier auszuschließen), so ist die (abschnittsweise definierte) Funktion
und sind hier auszuschließen), so ist die (abschnittsweise definierte) Funktioneine bzw. die stetige Fortsetzung von f (auf
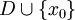 ).
).Es ergibt sich also als Kriterium: f ist genau dann in x0 stetig fortsetzbar, wenn der Grenzwert
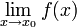 existiert.
existiert.Beispiel
Gegeben sei
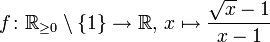 .
.
Die Funktion f ist in x0 = 1 stetig fortsetzbar:
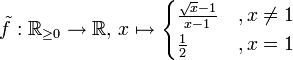 .
.
An diesem Beispiel kann man noch bemerken, dass
 auch ohne Fallunterscheidung geschrieben werden kann, es gilt nämlich
auch ohne Fallunterscheidung geschrieben werden kann, es gilt nämlich 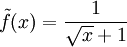 für alle
für alle 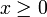 . In anderen Fällen kann es sein, dass die Fallunterscheidung unumgänglich ist. So hat etwa
. In anderen Fällen kann es sein, dass die Fallunterscheidung unumgänglich ist. So hat etwadie stetige Fortsetzung
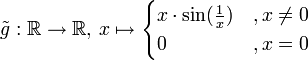 .
.
Spezialfall rationaler Funktionen
Gebrochen rationale Funktionen, deren Nenner und Zähler an derselben Stelle Null werden, können nach dem folgenden Verfahren stetig ergänzt werden.
Rationale Funktionen der Mathematik haben die Form
wobei u(x) und v(x) Polynomfunktionen sind.
Da u(x) und v(x) Polynome sind, ist ihr Verhalten an ihren Nullstellen bekannt: die Nullstellen der Zähler- und Nennerfunktionen lassen sich ausfaktorisieren. Wenn also u(x) und v(x) an der Stelle x0 eine Nullstelle haben, so ist immer
und
wobei
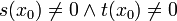 .
.
Die Terme Nu und Nv bezeichnet man auch als die Ordnung der jeweiligen Nullstelle.
Offensichtlich kann man die gemeinsamen Faktoren der Nullstellen kürzen.
- Wenn Nu > Nv > 0, dann liegt eine stetig behebbare Definitionslücke vor, wobei der Grenzwert durch 0 gegeben ist.
- Wenn Nu = Nv > 0, dann liegt eine stetig behebbare Definitionslücke vor, wobei der Grenzwert durch s(x0) / t(x0) gegeben ist.
- Wenn Nu < Nv, dann liegt eine Polstelle vor.
Beispiel
Die Funktion
hat für x = -1 eine Lücke, die sich durch Kürzen mit dem Wert -1/2 beheben lässt.
Differenzierbare Funktionen (Regel von L’Hôpital)
Wenn sowohl die Zähler- als auch die Nennerfunktion an der gemeinsamen Nullstelle differenzierbar sind, gilt die folgende Regel von L’Hospital:
Beispiel
Die Funktion
ist für x = 0 nicht definiert. Anwendung der l'Hospital-Formel (Differenzierung des Sinus ergibt den Kosinus) ergibt
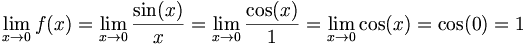 .
.
Die Lücke kann also durch den Wert 1 behoben werden.
Allgemeine Funktionen
Aussagen zu allgemeinen Funktionen sind nicht möglich. Unstetige Funktionen können ein beliebiges Verhalten zeigen, und sind individuell zu untersuchen.
Es kann beispielsweise vorkommen, dass eine Definitionslücke zwei unterschiedliche (einen linksseitigen und einen rechtsseitigen) Grenzwerte besitzt. In diesem Fall hat die Funktion eine Sprungstelle, und die Definitionslücke ist nicht stetig behebbar, obwohl keine Polstelle vorliegt.
Wikimedia Foundation.