Zahldarstellungssystem

Ein Zahlensystem wird zur Darstellung von Zahlen verwendet. Eine Zahl wird dabei nach den Regeln des jeweiligen Zahlensystems als Folge von Ziffern dargestellt.

Die moderne Forschung unterscheidet zwischen additiven, hybriden und positionellen Zahlensystemen.

Additionssysteme

In einem Additionssystem wird eine Zahl als Summe der Werte ihrer Ziffern dargestellt. Dabei spielt die Position der einzelnen Ziffern keine Rolle.

Ein Beispiel ist das Strichsystem (Unärsystem), das sich anbietet, wenn etwas schriftlich mitgezählt werden soll (wie zum Beispiel die Getränke auf einem Bierdeckel). Hierbei wird die Zahl n durch n Striche dargestellt. Dies ist vermutlich eines der ältesten Zählsysteme überhaupt. Das Unärsystem wird bei der Darstellung größerer Zahlen sehr schnell unübersichtlich. Deshalb ist es meist üblich, die Zahlen in Blöcke zusammenzufassen, indem man etwa jeden fünften Strich quer über die vier vorangegangenen Einzelstriche legt. Obwohl es aus diesem Grund nicht geeignet ist große Zahlen darzustellen, wird es im Alltag dennoch in manchen Situationen verwendet. Eine Addition um einen Zahlenwert ist einfach durch das Hinzufügen eines Striches möglich. Herkömmliche Systeme lassen eine so einfache und schnelle Erweiterung im Allgemeinen nicht zu.

Entwickelte Additionssysteme

Verschiedene Ziffern für jede Einheit der verschiedenen Potenzen der Basis

Ein derartiges Zahlensystem wurde schon vor ca. 5000 Jahren im alten Ägypten mit den Hieroglyphenzahlen verwendet.

Das Prinzip dieses Systems setzt für jede Potenz der Basis eine Ziffer, also z. B.: E=1, Z=10, H=100 und T=1000.
Die einzelnen Stellen wurden zumeist graphisch geordnet; im folgenden, prinzipiellen Beispiel nach den Dominoaugen.

                 HHH  ZZZ    E
 1982   =    T   HHH  Z Z    
                 HHH  ZZZ  E

In Susa wurde fast zeitgleich – also noch während der proto-elamitischen Epoche – ein solches Zahlensystem entwickelt, genauso wie – ab dem zweiten vorchristlichen Jahrtausend – von den Minoern auf Kreta, sowie etwas später auch von den Hethitern. Von meso-amerikanischen Hochkulturen sind Zahlensysteme nach diesem Prinzip ebenfalls bekannt.

Der Nachteil dieses Systems ist, dass jede Stelle aus der analogen Wiederholung des gleichen Zeichens besteht, weshalb die alten Ägypter schon Mitte des dritten Jahrtausends jede Stelle hieratisch-handschriftlich zu einer einzigen Ziffer zusammenzogen. Diese hieratischen Zahlen dienten den späteren alphabetischen Zahlen zum Vorbild.

Mehrere Ziffern innerhalb der verschiedenen Potenzen der Basis

Die Verwendung eigener Zeichen für die „Halbzahlen“ verhindern eine allzu häufige Wiederholung des gleichen Zeichens.

Ein Beispiel hierfür bilden die Römischen Zahlen, welche neben den Buchstaben I, X, C und M als Symbole für 1, 10, 100 und 1000, ebenso auch V, L und D für 5, 50 und 500 benutzen.

Die Ziffern werden mit abnehmender Wertigkeit geschrieben und addiert. 1776 wird zum Beispiel als MDCC.LXXVI dargestellt. Um die Zahlen noch ein wenig kürzer zu halten, wurde das System später so modifiziert, dass jede Ziffer nur dreimal hintereinander auftreten darf. Steht eine kleinere Ziffer vor einer größeren, so wird die erstere von der letzteren abgezogen. So wurde VIIII zu IX. Diese Subtraktionsregel innerhalb des Additionssystems wird aber nicht immer beherzigt.

In Westeuropa wurde das römische Zahlensystem bis ins 15. Jahrhundert allgemein verwendet.

Jede Grundzahl innerhalb der verschiedenen Potenzen der Basis hat eine eigene Ziffer

Bereits die hieratischen Zahlen (s. o.) gehorchten dem Prinzip der (im Dezimalsystem) jeweils neun verschiedenen Ziffern für jede verwendete Potenz der Basis.

Mitte des vierten vorchristlichen Jahrhunderts schufen die alten Griechen, ausgehend von diesen hieratischen Zahlen, die sogenannten alphabetischen Zahlen, indem sie die ersten 3×9 hieratischen Zahlen durch die Buchstaben ihres Alphabets ersetzten. Mittels der hybriden Verwendung der akrophonen Zahlen können auch große Zahlen dargestellt werden.

Außer in den weströmischen Gebieten, wo man stets an den römischen Zahlen festhielt, dominierte dieses progressive System – in ihren Adaptierungen an die jeweiligen Alphabete – sehr lange die Wissenschaft und Verwaltung von Persien, Armenien, Georgien, Arabien, Äthiopien, des Byzantinischen Reiches und des alten Russlands. Erst die indischen Ziffern lösten das System, nach viertausendjähriger Dominanz, allmählich ab. Im arabischen Raum schon Ende des ersten Jahrtausends, sonst erst Mitte des zweiten Jahrtausends.

Hybridsysteme

Hierbei wird eine Grundziffer einem Zeichen vorangestellt, das eine Potenz der Basis wiedergibt; die Werte beider werden miteinander multipliziert. In den europäischen Zahlensystemen kamen solche Hybridsysteme so gut wie nicht vor, wohl aber, schon seit Beginn des zweiten Jahrtausends v. Chr., in Mesopotamien, später auch in China und im Nahen Osten allgemein. Sowohl aus Äthiopien, als auch aus Südindien und Ceylon, sowie der Maya-Kultur sind solche hybriden Zahlensysteme bekannt.

Stellenwertsysteme

In einem Stellenwertsystem (Positionssystem) bestimmt die Stelle (Position) den Wert der jeweiligen Ziffer. Die „niederwertigste“ Position steht dabei im Allgemeinen rechts.

Ein Stellenwertsystem hat eine Basis b. Jede Zifferposition hat einen Wert, der einer Potenz der Basis entspricht. Für die n-te Position hat man einen Wert von b^n-1.

Die Berechnung des Zahlenwertes erfolgt durch Multiplikation der einzelnen Ziffern z_i mit den zugehörigen Stellenwerten bⁱ und Summation dieser Produkte:

Zahlenwert = $z_n \cdot b^n + \ldots + z_i \cdot b^i + \ldots + z_0 \cdot b^0$.

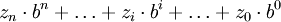Eigenschaften

• Für die Darstellung werden Ziffern benötigt, die von 0 bis b − 1 laufen.
• Die Zifferposition bestimmt den Stellenwert bⁿ.
• Zwei benachbarte Stellenwerte unterscheiden sich um den Faktor b.
• Der Zahlenwert ergibt sich aus der Summation aller Ziffernwerte, welche zuerst mit ihrem entsprechenden Stellenwert multipliziert worden sind.
• Mit der Beschränkung des niedrigsten Exponenten auf 0 kann man nur ganze Zahlen darstellen. Lässt man auch negative Exponenten zu, kann man auch rationale Zahlen in einem Stellenwertsystem schreiben, wobei der Übergang vom nichtnegativen zum negativen Exponenten durch ein Trennzeichen markiert wird, beispielsweise ein Komma:

$1 \cdot 10^3 + 2 \cdot 10^2 + 3 \cdot 10^1 + 4 \cdot 10^0 + 5 \cdot 10^{-1} + 6 \cdot 10^{-2} = 1234,56$

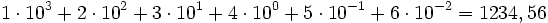
• Die Ziffern einer rationalen Zahl p/q erhält man durch das Verfahren der schriftlichen Division. Im Zehner-System spricht man auch von Dezimalbruch-Entwicklung. Hat q zur Basis b teilerfremde Primfaktoren, bricht die schriftliche Division nicht ab, sondern liefert eine sich wiederholende Folge von Ziffern. Diese wird Periode genannt und durch Überstreichen gekennzeichnet, z. B.

$\frac{5}{6} = 0{,}83333\ldots = 0{,}8\overline{3}$.

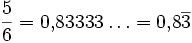• Die Basis b muss nicht notwendigerweise eine natürliche Zahl sein. Es wurde nachgewiesen, dass sämtliche komplexen Zahlen mit Betrag größer 1 als Basis eines Stellenwertsystems verwendet werden können. Ebenso sind Zahlensysteme mit gemischten Basen möglich. Beispiele hierfür findet man in Knuth: The Art of Computer Programming.
• Eine andere Darstellung für rationale und irrationale Zahlen ist der Kettenbruch, welcher bessere Approximationen liefert als die Stellenwertsysteme.

Literatur

• Georges Ifrah: Universalgeschichte der Zahlen. 2. Auflage. Campus-Verlag, Frankfurt/Main 1987, ISBN 3-593-33666-9. 
• John D. Barrow: Warum die Welt mathematisch ist. Campus-Verlag, Frankfurt/Main 1993, ISBN 3-593-34956-6. 

Weblinks

• Online-Umrechner für verschiedene Zahlensysteme (JavaScript)
• Online-Umrechner für Dezimal-/römische Zahlen (JavaScript, GPL)
• Online-Tool zum gleichzeitigen Konvertieren der Zahlensysteme (PHP)

Zahlensysteme

Ägyptisch | Arabisch | Armenisch | Attisch | Babylonisch | Brahmi | Chinesisch | Etruskische | Glagolitisch | Griechisch | Hebräisch | Indisch | Japanisch | Khmer | Koreanisch | Kyrillisch | Maya | Römisch | Sanskrit | Thai