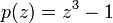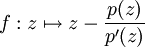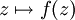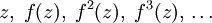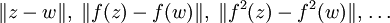Newtonfraktal

Das Newton-Fraktal zu $p(z)=\!\,z^3-1$

Das Newton-Fraktal zu einer nicht-konstanten meromorphen Funktion p ist eine Teilmenge der komplexen Zahlen. Es ist die Julia-Menge 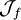$\mathcal J_f$ zur Funktion

$f : z\mapsto z-\frac{p(z)}{p'(z)}$

Das Newton-Verfahren zum Auffinden von Nullstellen, angewandt auf die Funktion p, führt nämlich zu der Iteration

$z \mapsto f(z)$

Abhängig vom Startwert z kann der Orbit von z

$z,\; f(z),\; f^2(z),\; f^3(z),\, \ldots$

ganz unterschiedliches Verhalten zeigen.

Anmerkung: Hier bezieht sich der Exponent auf f als Funktion, und nicht auf deren Funktionswert. f ⁿ bedeutet also n-malige Anwendung von f.

Dazu wählt man eine zweite komplexe Zahl w in einer Umgebung von z und vergleicht deren Orbits. Dann gibt es genau zwei Möglichkeiten, wie sich die Folge

$\|z-w\|,\; \|f(z)-f(w)\|,\;\|f^2(z)-f^2(w)\|,\, \ldots$

verhalten kann:

1. Es gibt eine Umgebung von z, so dass für jedes w aus dieser Umgebung die Folge gegen null konvergiert.
2. In jeder noch so kleinen Umgebung von z gibt es ein w, so daß die Folge nicht gegen Null konvergiert.

Im ersten Falle liegt z in der Fatou-Menge 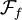$\mathcal F_f$. Im zweiten Falle liegt z in der Julia-Menge 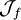$\mathcal J_f$. Da Julia-Mengen bis auf einige ausgezeichnete Ausnahmen Fraktale sind und sich f aus dem Newton-Verfahren für p ableitet, nennt man 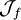$\mathcal J_f$ auch Newton-Fraktal von p.

Bedeutung für das Newton-Verfahren

Liegt der Startwert der Newton-Iteration nahe an einer einfachen Nullstelle von p, dann konvergiert das Verfahren quadratisch gegen diese Nullstelle. Bei einer mehrfachen Nullstelle ist das Newton-Verfahren immerhin noch linear konvergent. Diese Fälle gehören zum Fall 1 von oben.

Je näher der Startwert jedoch am Newton-Fraktal liegt, desto unüberschaubarer ist das Resultat des Newton-Verfahrens:

• Selbst Startwerte, die weit von einer Nullstelle entfernt liegen, können zu dieser hin konvergieren, auch wenn andere Nullstellen wesentlich näher am Startwert liegen (zu Fall 1).
• Es gibt Startwerte, die nicht gegen eine Nullstelle konvergieren, sondern lediglich gegen einen periodischen Zyklus (zu Fall 1). Ein Beispiel dafür ist das Polynom z³ − 2z + 2. Hier gibt es Startwerte, die vom anziehenden Zyklus {0,1} eingefangen werden.
• Liegt der Startwert im Newton-Fraktal selbst, dann konvergiert er nicht gegen eine Nullstelle (zu Fall 2).

Für nicht-konstante meromorphe Funktionen ist das Newton-Fraktal eine Nullmenge, das heißt, es ist eine Menge vom Maß Null. Das Newton-Verfahren führt also für fast alle Startwerte zu einem anziehenden, periodischen Zyklus von f hin. Falls dieser Zyklus Periodenlänge 1 hat, dann handelt es sich dabei um eine Nullstelle von p. Ansonsten ist das Newton-Verfahren für diesen Startwert nicht konvergent. Obwohl das Newton-Fraktal eine Nullmenge ist, kann es also ganze Gebiete geben, in denen das Verfahren nicht gegen eine Nullstelle konvergiert.

Diese Feststellung gilt auch für reellwertige rationale Funktionen. Wiederum dient das Polynom z³ − 2z + 2 als Beispiel. Weil es reelle Koeffizienten hat, bleiben die Werte der Newton-Iteration für reelle Startwert reellwertig. Da die reelle Achse durch Gebiete der Nichtkonvergenz verläuft, gibt es Intervalle, für die keine Konvergenz vorliegt. Von solchen Intervallen gibt es unendlich viele.

Beispielfraktale

Beispielfraktale

Das Newton Fraktal (in weiß) zu z3 − 2z + 2 farbcodiert nach Konvergenzgeschwindigkeit und den drei Nullstellen. Startwerte, die in den beige gezeichneten Gebieten liegen, konvergieren gegen die gleiche Nullstelle (im Bild links in hellbeige), analog für das grüne und das blaue Gebiet. Die Nullstellen zum grünen bzw. blauen Gebiet liegen symmetrisch zur waagerechten Symmetrieachse rechts im Bild. Je schneller ein Startwert zu seiner Nullstelle konvergiert, desto heller ist er eingefärbt. Die Werte in den unendlich vielen roten Bereichen konvergieren nicht gegen einen Nullstelle, sondern werden vom anziehenden Zyklus {0,1} eingefangen. Das Newton-Fraktal – im Bild als helle Struktur erkennbar – ist nicht beschränkt. In den drei zu erkennenden Richtungen reicht es bis nach ∞.

Newton-Fraktal zu einem Polynom mit 7 zufällig gewählten Nullstellen (weiße Punkte), der Bereich stellt − 1 < Rez,Imz < 1 dar. Das Fraktal selbst ist z.B. der Rand des gelben Gebietes. Ebenso ist es der Rand des grünen Gebietes, der Rand des türkisfarbenen Gebietes, etc. Diese Eigenschaft ist allen Julia-Mengen gemein. Die Farben rot und pink wurden doppelt verwendet, so dass die Grenze des roten und des pinkfarbenen Gebietes nicht dem Newton-Fraktal entsprechen.

Weblinks

Quellen

• J. H. Hubbard, D. Schleicher, S. Sutherland: How to Find All Roots of Complex Polynomials by Newton's Method Preprint (2000), Inventiones Mathematicae vol. 146 (2001) – mit Diskussion der Struktur von Newton-Fraktalen