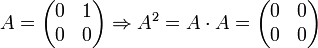Nilpotenzindex

Die nilpotente Matrix und der nilpotente Endomorphismus sind Begriffe aus dem mathematischen Teilgebiet der linearen Algebra. Dabei bezeichnet man eine quadratische Matrix als nilpotent, wenn eine ihrer Potenzen die Nullmatrix ergibt:

Aⁿ = 0 für ein $n \in \N$

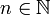
Entsprechend bezeichnet man einen Vektorraum-Endomorphismus f als nilpotent, wenn es eine Zahl 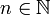$n \in \N$ gibt, sodass fⁿ die Nullabbildung ist. Die Zahl n bezeichnet man als Nilpotenzgrad oder Nilpotenzindex.

Ein Beispiel für eine nilpotente Matrix ist die Matrix

$A=\begin{pmatrix} 0 & 1 \\ 0 & 0 \end{pmatrix} \Rightarrow A^2 = A \cdot A = \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix}$

Zwischen nilpotenten Matrizen und nilpotenten Endomorphismen gibt es einen Zusammenhang: die nilpotenten Matrizen sind die Darstellungsmatrizen der nilpotenten Endomorphismen.

Äquivalente Definitionen

Zu der Aussage, dass eine $n \times n$-Matrix A nilpotent mit dem Nilpotenzgrad k ist, sind folgende Aussagen äquivalent:

• A^k = 0 und $A^{k-1} \neq 0$.
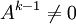• das charakteristische Polynom von A hat die Form χ_A(λ) = det(λE − A) = λⁿ.
• A ist ähnlich zu einer echten oberen Dreiecksmatrix:

  $A = P^{-1} \begin{pmatrix}0 & b_{1,2} & \cdots & b_{1,n} \\ 0 & \ddots & \ddots & \vdots \\ \vdots & \ddots & \ddots & b_{n-1,n} \\ 0 & \cdots & 0 & 0\end{pmatrix} P$

Eigenschaften nilpotenter Matrizen

Wenn eine Matrix A nilpotent ist, wobei n die kleinste natürliche Zahl mit Aⁿ = 0 ist, dann...

• hat sie genau einen Eigenwert, nämlich Null. Das folgt direkt aus der Form des charakteristischen Polynoms (siehe oben), dessen Nullstellen die Eigenwerte sind.
• ist sie nicht invertierbar, da einer ihrer Eigenwerte Null ist.
• ist A=0 oder sie ist nicht diagonalisierbar, da Diagonalmatrizen ungleich 0 nicht nilpotent sind.
• ist die Determinante Null: det(A) = 0.
• ist die Spur Null.
• hat sie keinen vollen Rang, d.h. ihre Spaltenvektoren sind linear abhängig. Es sind jedoch nicht alle quadratischen Matrizen mit linear abhängigen Spalten auch gleichzeitig nilpotent.
• ist (E − A) immer invertierbar (E ist die Einheitsmatrix): Es ist (E − A)(E + A + A² + ... + A^{n − 1}) = E − Aⁿ = E.

Da eine nilpotente Matrix ein Spezialfall eines nilpotenten Elements eines Ringes ist, gelten die im Artikel Nilpotenz gegebenen allgemeinen Aussagen auch hier.