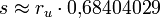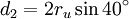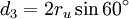Nonagon

regelmäßiges Neuneck

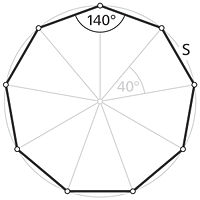
Ein Neuneck (Nonagon, seltener: Enneagon) ist eine geometrische Figur. Es gehört zur Gruppe der Vielecke (Polygone). Es ist definiert durch neun Punkte. Dieser Artikel beschäftigt sich im Weiteren ausschließlich mit regelmäßigen Neunecken (siehe Bild); ein Polygon heißt regelmäßig, wenn es konvex ist, alle Seiten gleich lang sind und seine Eckpunkte auf einem gemeinsamen Umkreis liegen.

Mathematische Zusammenhänge

Formel für Winkelberechnungen

Der Winkel, den zwei benachbarte Seitenkanten im ebenen, regelmäßigen Neuneck miteinander einschließen, beträgt nach einer allgemeinen Formel für regelmäßige Polygone, in der für die Variable n die Anzahl der Eckpunkte des Polygons eingesetzt werden muss (in diesem Fall: n = 9):

$\alpha =\frac{(n - 2)}{n} \cdot 180^\circ = \frac{7}{9} \cdot 180^\circ = 140^\circ$

Der spitze Winkel eines der neun Teildreiecke beträgt 360°/ 9 = 40°.

Formel für die Fläche A

Ein Neuneck besitzt einen eindeutig bestimmbaren Flächeninhalt, welcher sich stets durch Zerlegen in Dreiecke berechnen lässt. Die Fläche des regelmäßigen Neunecks beträgt das Neunfache der Fläche eines jener Dreiecke, die von seinem Mittelpunkt und je zwei benachbarten Eckpunkten aufgespannt werden.

$A = \frac{9}{4} \cdot s^2 \cdot \frac{\cos 20^\circ}{\sin 20^\circ}$

oder mit dem Umkreisradius:

$A = \frac{9}{2} \cdot r_u^2 \cdot \sin 40^\circ$

Formel für die Seitenlänge s

$s = 2 \cdot r_u \cdot \sin{20^\circ}$

$s \approx r_u \cdot 0{,}68404029$

Diagonalen

Es gibt drei Typen von Diagonalen, die zwei, drei bzw. vier Seiten einschließen. Ihre Längen betragen:

$d_2=2r_u\sin 40^\circ$

$d_3=2r_u\sin 60^\circ$

$d_4=2r_u\sin 80^\circ$

Die Differenz d₄ − d₂ zwischen den Längen der längsten und der kürzesten Diagonalen ist gleich der Seitenlänge s.

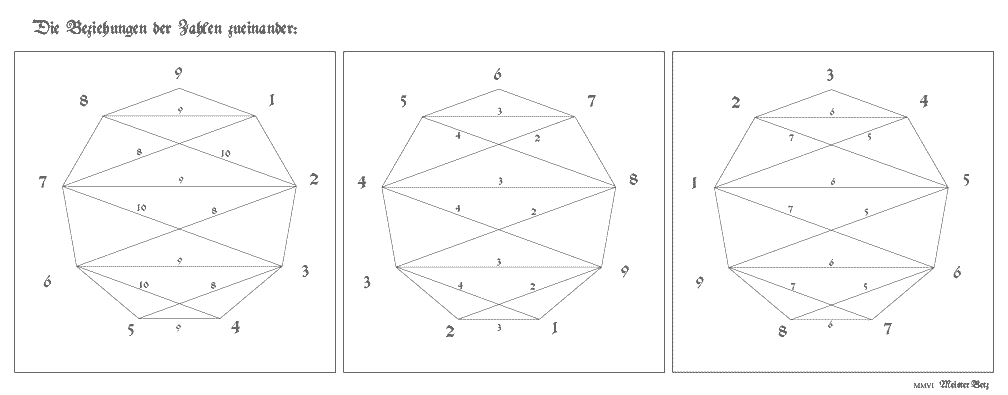
Beziehungen der Zahlen innerhalb des Enneagons (Teil 1)

Im Neuneck entstehen folgende Beziehungen der Zahlenwerte von 1 bis 9. Als Beispiel im ersten Bild: 8+1 =9, 7+2 =9, 6+3 =9, 5+4 =9 (horizontale Verbindungen), während 6+4, 7+3, 8+2 und 9+1 jeweils die Summe 10 ergeben. (Parallele Verbindungslinien führen zu gleichem Ergebnis.)

Näherungskonstruktionen

Ein regelmäßiges Neuneck kann nicht konstruiert, sondern nur berechnet werden, da der 40°-Winkel mit Zirkel und Lineal nicht konstruiert werden kann ^[1]. Es gibt jedoch einige für die Praxis ausreichend genaue Näherungskonstruktionen.

Erste Konstruktion

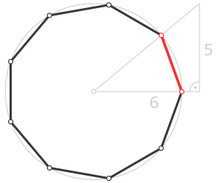
Bei der einfachsten Näherungskonstruktion wird ein rechtwinkliges Dreieck mit den Katheten 6 und 5 verwendet.

$\arctan\frac{5}{6}\approx 39{,}80557 ^\circ$

Mit diesem Dreieck erhält man einen Winkel von ca. 39,80557°.

Ein wesentlich besseres Ergebnis erreicht man mit einem Dreieck der Seitenlängen 87 und 73, das einen Winkel von ca. 39,99936° liefert:

$\arctan\frac{73}{87} \approx 39{,}99936^\circ$

Da der Winkel 40° betragen müsste, ist in beiden Fällen das Ergebnis für die Seitenlänge kleiner als der wahre Wert. Beim 6:5-Dreieck beträgt der rel. Fehler F:

$F = 2 * \sin \frac{\arctan \frac{5}{6}} {2} - 2 * \sin(20^\circ) \approx 0{,}00319$

Das sind also 0,319 Prozent. Beim 87:73-Dreieck beträgt er ca. -0.0000106, also 0,00106 Prozent oder 1/1000 Prozent. Anders formuliert: Neunecke, die mit dem großen Hilfsdreieck konstruiert werden, müssen einen Umkreisradius von mehr als 94,591 Metern haben, damit der Fehler der Seitenlänge größer als 1 Millimeter ist. Ein solches Neuneck wäre größer als dreieinhalb Fußballfelder. Die Konstruktion mit dem großen Dreieck ist in der Praxis aber kaum realisierbar, denn jeder Zirkel ist fehlerbehaftet, und beim Abtragen von 87 Strecken kann sich der Fehler im ungünstigsten Fall vervielfältigen.

Zweite Konstruktion

Eine wesentlich praktikablere Konstruktion wird wie folgt durchgeführt:

1. Zeichne um einen Punkt M den Umkreis des Neunecks (k₁).
2. Zeichne einen Durchmesser AN und verlängere die Strecke auf das Dreifache.
3. Trage auf dieser Geraden vier weitere Radien ab. Von Punkt A also insgesamt 6 Radien bis Punkt S.
4. Zeichne über AS einen Thaleskreis (k₂)
5. Trage mit einem Bogen um Punkt A (k₃) einen Abstand von 5 Radien am Thaleskreis ab (Punkt T).
6. Trage mit einem Bogen um Punkt S (k₄) den Abstand TS auf der Geraden ab (Punkt U).
7. Die NU = s ist eine gute Näherung für die Seite des Neunecks.

Die Strecke s hat eine Länge von

$r \cdot \left(4 -\sqrt{11} \right) \approx r \cdot 0{,}68337521$

Bei dieser Konstruktion beträgt der Fehler also

$\frac{0{,}68337521 - 0{,}68404029} {0{,}68404029} \approx -0{,}000972 = -0{,}097$%

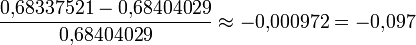Das entspricht bei einem Radius von 150,3 cm einer Abweichung von -1 mm. Die Seite ist also etwas zu kurz.

Dürer-Konstruktion

Eine noch elegantere, aber leider ungenauere Näherungskonstruktion hat bereits Albrecht Dürer (1471–1528) verwendet.

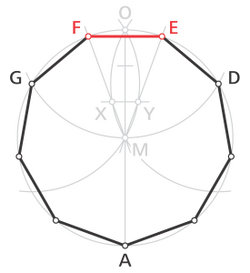
1. Auf dem Umkreis des Neunecks mit Mittelpunkt M und Radius r markiert man den Eckpunkt A.
2. Dann schlägt man einen Kreis mit demselben Radius r um den gegenüberliegenden Kreispunkt O und erhält die beiden Eckpunkte D und G. (Anmerkung: Diese beiden Eckpunkte sind exakt, da die Diagonalen des Neunecks zwischen A, D und G ein gleichseitiges Dreieck ergeben. Die Punkte E und F können nicht mehr genau konstruiert werden, da das Problem der Dreiteilung des Winkels nur für spezielle Einzelfälle, nicht aber allgemein und auch nicht für den vorliegenden Fall von 120° lösbar ist.)
3. Nun schlägt man wiederum mit dem Radius r zwei Kreise um die Punkte D und G.
4. Als nächstes wird die Strecke OM in drei Teile geteilt. Durch den Teilungspunkt, der näher beim Mittelpunkt des Neunecks liegt, wird ein Lot (horizontale Linie) auf die Gerade OM gezeichnet.
5. Die Schnittpunkte dieses Lotes mit den Kreislinien um D und G ergeben die Punkte X und Y.
6. Schließlich verlängert man die Geraden MX und MY bis sie den Umkreis schneiden. Diese Schnittpunkte sind eine gute Näherung für die Eckpunkte E und F. Die Strecke EF ist eine gute Näherung für die Seitenlänge des Neunecks.
7. Die Eckpunkte B, C, H und I erhält man durch Abschlagen der so gewonnenen Seitenlänge auf der Kreislinie.

Wie eingangs erwähnt ist diese Konstruktion relativ ungenau. Das Dreieck MEF hat einen spitzen Winkel von ca. 39,59407° statt 40°. Die Strecke EF ist deswegen um ca. 0,97% kürzer als der wahre Wert der Seitenlänge.

Verwendung des Neunecks in der Praxis

Die jährlich erscheinenden 5-Euro Silber Euromünzen aus Österreich haben die Form eines Neunecks^[2]. Außerdem basiert die Architektur der Häuser der Andacht (die Sakralbauten der Bahai) auf einem Neuneck. Sternmotoren wurden meistens 5-, 7- oder 9-zylindrig gebaut.

Quellen

1. ↑ Emil Artin: Galoissche Theorie. Verlag Harri Deutsch, Zürich 1973, ISBN 3-87144-167-8, S 85.
2. ↑ Oesterreichische Nationalbank: Münzbroschüre Ausgabe 2006 (pdf)

Weblinks

• Weitere mathematische Details zum Neuneck