Normalformspiel

Die Normalform bezeichnet in der Spieltheorie eine Darstellungsform von Spielen, die sich im Wesentlichen auf die A-Priori-Strategiemengen der einzelnen Spieler und eine Auszahlungsfunktion als Funktion der gewählten Strategiekombinationen beschränkt. Gerecht wird diese Darstellungsform am ehesten solchen Spielen, bei denen alle Spieler ihre Strategien gleichzeitig und ohne Kenntnis der Wahl der anderen Spieler festlegen.

Eine Alternative ist die Extensivform, deren Stärke in der anschaulichen Darstellung zeitlicher oder logischer Abfolgen liegt.

Die Normalform für Spiele wurde erstmals von Émile Borel (1921) und John von Neumann (1928) beschrieben, die erkannten, dass im Prinzip jedes Strategiespiel in eine solche Form transformiert werden kann.

Definition

Die Normalform eines Spiels ist ein Tupel Γ = (N,Σ,u) mit den folgenden Elementen:

Menge der Spieler

$N = \{1, 2, \ldots, n\}$

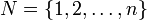
Strategieraum

$\Sigma = \Sigma_1 \times \Sigma_2 \times \ldots \times \Sigma_n$

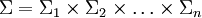
Σ_i bezeichnet die Strategiemenge des Spielers i, aus der er seine Züge wählen kann.

Nutzenfunktion

$u:\Sigma \to \R^n$

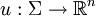
Dabei ist 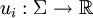$u_i:\Sigma \to \R$ die Nutzenfunktion des Spielers i. Abhängig von der eigenen Strategie und der Strategie der anderen Spieler hat der Spieler einen Nutzen oder eine Auszahlung von $u_i(\sigma_1,\ldots,\sigma_i,\ldots, \sigma_n)$.

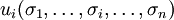Gemischte und reine Strategien

In den so genannten reinen Strategien wählen die Spieler genau ein 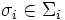$\sigma_i \in \Sigma_i$. Für manche Spiele ist es jedoch notwendig, den Spielern zusätzlich die Möglichkeit einzuräumen, zufällig die Strategien auszuwählen und zuvor lediglich die Wahrscheinlichkeitsverteilung über Σ_i anzugeben, mit denen die einzelnen 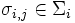$\sigma_{i,j}\in\Sigma_i$ ausgewählt werden. Dabei bezeichnet s_i die Parameter dieser Wahrscheinlichkeitsverteilung und S_i die Menge der möglichen Parameterkombinationen.

Ist Σ_i endlich beziehungsweise abzählbar, so ist s_i ein Vektor, wobei s_i,j die Wahrscheinlichkeit angibt, dass die Strategie σ_i,j gewählt wird.

Darstellung in Tabellenform

Bimatrix (Kampf der Geschlechter)

Werden nur Spiele mit 2 Spielern, N = {1,2}, betrachtet und sind die Strategiemengen Σ_1,2 endlich und überschaubar, kann man ein Spiel in Normalform auch als Tabelle darstellen:

Spieler 1\Spieler 2	σ2,1	σ2,2
σ1,1	(3,3)	(1,2)
σ1,2	(2,1)	(1,1)

In diesem Fall bezeichnet die erste Zahl in der Klammer die Auszahlung des Spielers 1 und die zweite Zahl die Auszahlung des Spielers 2 bei der entsprechenden Strategienkombination. Wählt Spieler 1 beispielsweise Strategie σ_1,1 und Spieler 2 σ_2,1, so erhalten beide jeweils eine Auszahlung in Höhe 3.