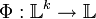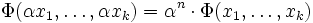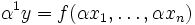Nullhomogenität

Eine mathematische Funktion heißt homogen vom Grad n, wenn bei proportionaler Änderung aller Variablen um den Proportionalitätsfaktor α sich der Funktionswert um den Faktor αⁿ ändert. Formal:

Eine Funktion auf dem k-dimensionalen reellen Vektorraum

$\Phi : \mathbb{L}^k \rightarrow \mathbb{L}$

heißt homogen vom Grad n genau dann, wenn für alle 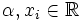$\alpha,x_i\in\mathbb{R}$ gilt

$\Phi(\alpha x_1,\ldots,\alpha x_k) = \alpha^n\cdot \Phi(x_1,\ldots,x_k)$

Funktionen dieses Typs sind wichtig z. B. in den Wirtschaftswissenschaften und in den Naturwissenschaften.

Beispiele aus den Wirtschaftswissenschaften

Individuelle Nachfragefunktionen x = x(p,E) stellen einen Zusammenhang zwischen Preisen p, Einkommen E und den nachgefragten Mengen x nach den Gütern dar. Kommt es z. B. im Zuge einer Währungsumstellung (von DM zu Euro) zu einer betragsmäßigen Halbierung aller Preise und der Einkommen und wird dieses von den Individuen vollständig berücksichtigt (Freiheit von Geldwertillusion), so werden sich die nachgefragten Mengen nicht ändern. Das heißt es gilt

α⁰x = x(αp,αE)

Nachfragefunktionen sind somit homogen vom Grad Null in den Variablen Preise und Einkommen (Nullhomogenität).

Produktionsfunktionen 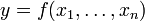$y=f(x_1,\dots, x_n)$ stellen einen Zusammenhang zwischen Inputs x_i und dem zugehörigem Output y her. Kommt es dann eventuell in der Chemieproduktion jeweils bei proportionalen Änderung (z. B. Verdoppelung) aller Inputs zu einer entsprechenden proportionalen Änderung (Verdoppelung) des Outputs so gilt:

$\alpha^1 y=f(\alpha x_1,\dots,\alpha x_n)$

Eine solche Produktionsfunktion wäre dann homogen mit dem Homogenitätsgrad 1 (linear homogen).

Eulersches Theorem

Der Eulersche Satz über homogene Funktionen stellt eine äquivalente Charakterisierung dar:

$n\cdot \Phi(x_1,\ldots,x_k) = \sum_{i=1}^k \frac{\partial\Phi}{\partial x_i}\cdot x_i \;\;\Leftrightarrow\;\; n\cdot \Phi(\vec{x}) = \vec{x}\cdot\nabla\Phi(\vec{x})$.

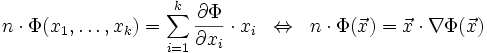Eine homogene Funktion kann also auf einfache Weise durch die partiellen Ableitungen und Koordinaten dargestellt werden.

Diese Tatsache wird in der Physik sehr häufig benutzt, vor allem in der Thermodynamik, da die dort auftretenden intensiven und extensiven Zustandsgrößen homogene Funktionen nullten bzw. ersten Grads sind.

In den Wirtschaftswissenschaften folgt aus dem Eulerschen Theorem für Produktionsfunktionen vom Homogenitätsgrad 1 bei den Faktorpreisen q_i und dem Güterpreis p

$y= f(x_1,\ldots,x_k) = \sum_{i=1}^k \frac{\partial f}{\partial x_i}\cdot x_i = \sum_{i=1}^k \frac{q_i}{p}\cdot x_i \;\;\Rightarrow\;\; p\cdot y = \sum_{i=1}^k q_i\cdot x_i$.

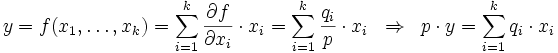Bei linear homogenen Produktionsfunktionen ist der Wert des Produkts gleich den Faktorkosten (Ausschöpfungstheorem).