Nöbeling

Georg Nöbeling (* 12. November 1907 in Lüdenscheid; † 16. Februar 2008 in Rosenheim; vollständiger Name August Georg Nöbeling) war ein deutscher Mathematiker.

Leben und Werk

Geboren und aufgewachsen in Lüdenscheid, studierte Nöbeling ab 1927 Mathematik und Physik an der Universität Göttingen und ab 1929 an der Universität Wien. Dort promovierte er im Jahr 1931 bei Karl Menger über eine Verallgemeinerung des Einbettungssatzes, dessen Darstellung im dreidimensionalen Raum als Menger-Schwamm bekannt ist.^[1]

Für Menger war Nöbeling bis 1933 als Hilfsassistent tätig, wo er in Mengers Mathematischem Kolloquium mit Kurt Gödel, Franz Alt, Abraham Wald, Olga Taussky-Todd und anderen zusammenwirkte.^[2] 1933 wurde er Assistent von Otto Haupt in Erlangen, nach der Habilitation 1935 wurde er 1940 zum außerordentlichen und 1942 zum ordentlichen Professor an der Universität Erlangen berufen. Seine Arbeitsschwerpunkte waren Analysis, Topologie und Geometrie. 1968/69 löste er das Speckersche Problem über Abelsche Gruppen.

Als Dekan (1950-1952) der naturwissenschaftlichen Fakultät, als Rektor (1961-1963) und als Baureferent bis zu seiner Emeritierung 1976 war er maßgeblich in der universitären Selbstverwaltung aktiv. Dabei prägte er insbesondere die Planung der Technischen Fakultät und die Fusion mit der Nürnberger Hochschule zur Universität Erlangen-Nürnberg.^[3]

1952-1953 und 1954-1955 war er Vorsitzender der Deutschen Mathematiker-Vereinigung; seit 1959 ist er Mitglied der Bayerischen Akademie der Wissenschaften. 1965 wurde er mit dem Bayerischen Verdienstorden ausgezeichnet.

Schriften (Auswahl)

• Georg Nöbeling: Über eine n-dimensionale Universalmenge im 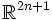$\mathbb{R}^{2n+1}$. In: Mathematische Annalen 104 (1931), S. 71-80.
• Georg Nöbeling: Grundlagen der analytischen Topologie. Berlin 1954.
• Georg Nöbeling: Verallgemeinerung eines Satzes von E. Specker. Inventiones mathematicae 6 (1968), S. 41-55.
• Georg Nöbeling: Einführung in die nichteuklidischen Geometrien der Ebene. Berlin 1976, ISBN 3-11-002001-7.
• Georg Nöbeling: Integralsätze der Analysis. Berlin 1979, ISBN 3-11-007433-9 (formal falsche ISBN); korrigierte ISBN 3-11-007433-8

Weblinks

• Literatur von und über Georg Nöbeling im Katalog der Deutschen Nationalbibliothek (Datensatz zu Georg Nöbeling • PICA-Datensatz • Einträge im Musikarchiv)

Quellen

1. ↑ Karl Sigmund: "Kühler Abschied von Europa - Wien 1938 und der Exodus der Mathematik", S. 16 f.
2. ↑ Quelle: http://www.math.iit.edu/Menger/menger.html
3. ↑ Quelle: http://www.uni-erlangen.de/infocenter/presse/pressemitteilungen/2007/nachrichten_2007/11_07/263noebeling.shtml

Personendaten
NAME	Nöbeling, Georg
ALTERNATIVNAMEN	Nöbeling, August Georg (vollständiger Name)
KURZBESCHREIBUNG	deutscher Mathematiker
GEBURTSDATUM	12. November 1907
GEBURTSORT	Lüdenscheid
STERBEDATUM	16. Februar 2008
STERBEORT	Rosenheim