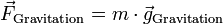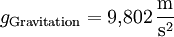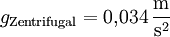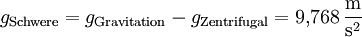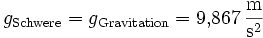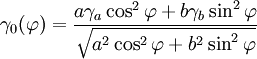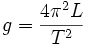Oberflächenbeschleunigung

Physikalische Größe
Name	Schwerebeschleunigung
Größenart	Beschleunigung
Formelzeichen der Größe	g
Größen- und Einheiten- system Einheit Dimension SI m · s−2 L · T−2 CGS cm · s−2 L · T−2 Planck Planck-Beschleunigung ħ−1/2 · G−1/2 · c7/2

Unter der Schwerebeschleunigung (auch: Fallbeschleunigung oder Ortsfaktor) versteht man die Beschleunigung, die ein Körper im freien reibungslosen Fall auf einer Planetenoberfläche erfährt, wenn zusätzlich zur Gravitationskraft auch eine Zentrifugalkraft auf den Körper wirkt. Mit Gravitationsbeschleunigung (auch Gravitationsfeldstärke) bezeichnet man hingegen die Beschleunigung, die ein Körper im freien reibungslosen Fall auf einer Planetenoberfläche erfährt, wenn keine zusätzlichen Kräfte auf den Körper einwirken. Die Schwerebeschleunigung eines (in der Regel rotierenden) Himmelskörpers ist folglich die Summe aus Gravitationsbeschleunigung und Zentrifugalbeschleunigung. Der schwereverringernde Beitrag der Zentrifugalbeschleunigung ist jedoch meist gering, weshalb der Betrag der Schwerebeschleunigung sich von dem der Gravitationsbeschleunigung nicht groß unterscheidet (siehe auch Tabelle Schwere- und Gravitationsbeschleunigung ausgewählter Himmelskörper).

Im Schwerebeschleunigung auf der Erdoberfläche – die sog. Erdschwerebeschleunigung – beträgt durchschnittlich g = 9,81 m · s⁻², variiert aber aufgrund der Zentrifugalbeschleunigung und der Erdgestalt regional um einige Promille.

Einheiten

Die SI-Einheit der Schwerebeschleunigung ist m · s⁻². Der millionste Teil davon ist 1 µm · s⁻², was etwa der Messgenauigkeit von Gravimetern entspricht.

Im alten CGS-Einheitensystem heißt die Einheit Gal (nach Galileo Galilei), das in der Gravimetrie und Angewandten Geophysik oft in 1.000 Milligal unterteilt wird:

1 Gal = 1 cm · s⁻² = 0,01 m · s⁻²

1 mGal = 10 µm · s⁻² = 10^-5 m · s⁻²

Manchmal dient die Erdschwerebeschleunigung g auch als Einheit. Im Mittel der Erde gilt dann genähert

1 g = 9,81 m · s⁻² = 981 Gal = 981.000 mGal.

Berechnung

Die Gravitationsbeschleunigung bestimmt die Gravitationskraft 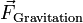$\vec F_\mathrm{Gravitation}$, mit der ein Körper der Masse m von einem Himmelskörper bzw. in einem Gravitationsfeld angezogen wird:

$\vec F_\mathrm{Gravitation} = m \cdot \vec g_\mathrm{Gravitation}$

Die Schwerkraft setzt sich aus der anziehend wirkenden Gravitationskraft und der abstoßend wirkenden Zentrifugalkraft zusammen.

$\vec F_\mathrm{Schwere} = \vec F_\mathrm{Gravitation} + \vec F_\mathrm{Zentrifugal}$

Für die Schwerebeschleunigung gilt dementsprechend:

$\vec g_\mathrm{Schwere} = \vec g_\mathrm{Gravitation} + \vec g_\mathrm{Zentrifugal}$

Am Äquator wirken Gravitationskraft und Zentrifugalkraft genau entgegengesetzt.

g_Schwere = g_Gravitation − g_Zentrifugal

Am Pol wirkt keine Zentrifugalkraft, da der Abstand von der Rotationsachse null ist.

g_Schwere = g_Gravitation

Die Gravitationsbeschleunigung lässt sich (für Punktmassen) aus der Masse M des Planeten und dem Abstand r vom Planetenzentrum (als Punktmasse) mit der Gravitationskonstanten G berechnen.

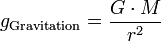$g_\mathrm{Gravitation} = \frac{G \cdot M}{r^2}$ mit $G=6{,}67428 \cdot 10^{-11}\,{\mathrm{m^3}\over\mathrm{kg\,s^2}}$

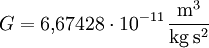
Die Zentrifugalbeschleunigung lässt sich aus Umlaufdauer T und Abstand r berechnen.

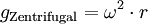$g_\mathr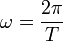m{Zentrifugal} = \omega^2 \cdot r$ mit $\omega = \frac{2 \pi}{T}$

Beispiel Erde

Die folgenden Berechnungen für die Gravitationsbeschleunigung liefern nur Näherungswerte, da die Newtonsche Gravitationsgleichung nur für Punktmassen gilt. Die Erde kann jedoch, bei Betrachtung von ihrer Oberfläche aus, nicht als Punktmasse modelliert werden. Darüber hinaus erfordert eine korrekte Berechnung der Gravitation an verschiedenen Punkten auf der Erde die Berücksichtigung der Schwereanomalien.

Für das einfache Modell eines Ellipsoides mit aller Masse im Zentrum aber gilt:

Masse: $M=5{,}974 \cdot 10^{24}\,\mathrm{kg}$

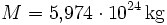
Äquatorradius: $r_\mathrm{\ddot{A}} = 6{,}378 \cdot 10^{6}\,\mathrm{m}$

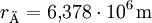
Polradius: $r_\mathrm{P} = 6{,}357 \cdot 10^{6}\,\mathrm{m}$

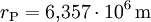
Rotationsdauer: $T = 0{,}9973 \mathrm{d} = 8{,}617 \cdot 10^{4}\,\mathrm{s}$

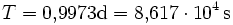
Am Äquator:

$g_\mathrm{Gravitation} = 9{,}802 \,{\mathrm{m}\over\mathrm{s^2}}$

$g_\mathrm{Zentrifugal} = 0{,}034 \,{\mathrm{m}\over\mathrm{s^2}}$

$g_\mathrm{Schwere} = g_\mathrm{Gravitation} - g_\mathrm{Zentrifugal} = 9{,}768 \,{\mathrm{m}\over\mathrm{s^2}}$

Am Pol:

g_Zentrifugal = 0

$g_\mathrm{Schwere} = g_\mathrm{Gravitation} = 9{,}867 \,{\mathrm{m}\over\mathrm{s^2}}$

Die Normalschwerewerte an der Erdoberfläche lassen sich mit der Formel von Somigliana genau berechnen. Hierbei wird die Form des Erdschwerefeldes durch ein Normalellipsoid angenähert.

$\gamma_0(\varphi) = \frac{a \gamma_a \cos^2 \varphi + b \gamma_b \sin^2 \varphi}\sqrt{a^2 \cos^2 \varphi + b^2 \sin^2 \varphi}$

mit den Parametern des Geodätische Referenzsystem 1980 (GRS 80) :

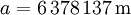$a = 6\,378\,137\,\mathrm{m}$ = große Halbachse (Äquatorradius)

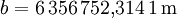$b = 6\,356\,752{,}314\,1\,\mathrm{m}$ = kleine Halbachse (Polradius)

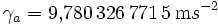$\gamma_a = 9{,}780\,326\,771\,5\,\mathrm m s^{-2}$ = Normalschwere am Äquator

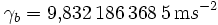$\gamma_b= 9{,}832\,186\,368\,5\,\mathrm m s^{-2}$ = Normalschwere am Pol

$\varphi$ = geographische Breite

Dies kommt den gemessenen Werten bereits sehr nahe. Eine noch bessere Beschreibung der Erdschwere muss auch weitere Asymmetrien in der Form der Erde berücksichtigen (siehe Artikel über Geoid).

Messung

Die Schwerebeschleunigung kann mit Gravimetern auf µGal genau gemessen werden.

Eine andere Methode beruht auf der Messung der Schwingungsdauer T eines Fadenpendels mit Fadenlänge L:

$g = \frac{4\pi^2 L}{T^2}$

Schwere- und Gravitationsbeschleunigung ausgewählter Himmelskörper

Folgende Tabelle vergleicht die Schwere- mit Gravitationsbeschleunigung der Erde mit Himmelskörpern unseres Planetensystems.

Himmelskörper	Gravitationsbeschleunigung[1] in m · s−2	Schwerebeschleunigung[1] in m · s−2 am Äquator	Äquatoriale Zentrifugalbeschleunigung [2]
Merkur	03,70	03,70	0,0
Venus	08,87	08,87	0,0
Erde	09,798	09,780	0,0339
Mars	03,71	03,69	0,0171
Jupiter	24,79	23,12	2,21
Saturn	10,44	08,96	1,67
Uranus	08,87	08,69	0,26
Neptun	11,15	11,00	0,29

Siehe auch

• Gravitationskonstante, kosmologische Konstante
• Beschleunigung, Erdschwerebeschleunigung
• Atwoodsche Maschine, Fallschnur
• Schwereanomalie, Schweregradient
• GRACE, ein Projekt zur genauen Bestimmung des Erdschwerefeldes in einer niedrigen Umlaufbahn

Einzelnachweise

1. ↑ ^{a b} David R. Williams: Planetary Fact Sheet - Metric. NASA, 29. November 2007. Abgerufen am 4. August 2008. (englisch, inkl. Unterseiten)
2. ↑ Deutschschweizerische Mathematikkommission (DMK) und Deutschschweizerische Physikkommission (DPK) (Hrsg.): Formeln und Tafeln. 11. Auflage. Orell Füssli Verlag AG, Zürich 2006, ISBN 978-3-280-02162-0, S. 188.