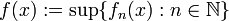Oberhalbstetig

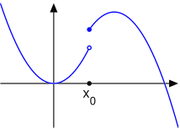
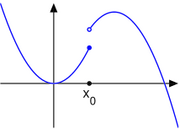
In der Mathematik heißt eine reellwertige Funktion f oberhalbstetig (oder halbstetig von oben) in einem Punkt x, wenn die Funktionswerte für Argumente nahe bei x von x ausgehend nicht nach oben springen. Wenn die Funktionswerte nicht nach unten springen, dann heißt die Funktion unterhalbstetig in x (oder halbstetig von unten).

Definition

Oberhalbstetige Funktion (der vollausgefüllte blaue Punkt gibt (x₀ | f(x₀)) an)

Sei X ein topologischer Raum, x in X und 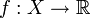$f: X \to \mathbb{R}$ eine reellwertige Funktion. f heißt in x₀ oberhalbstetig, wenn für jedes ε > 0 eine Umgebung U von x₀ existiert, so dass f(y) < f(x₀) + ε für alle y in U gilt. Ist X ein Raum, in dem jede folgenstetige Funktion auch stetig ist, etwa ein metrischer Raum, so ist f genau dann oberhalbstetig in x, falls

$\limsup_{y\to x} f(y) \le f(x)$.

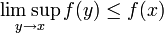f heißt oberhalbstetig auf einer Teilmenge M von X, wenn sie in jedem Punkt 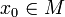$x_0\in M$ oberhalbstetig ist. Ist dabei M der ganze topologische Raum X, so heißt f oberhalbstetig.

Unterhalbstetige Funktion (der vollausgefüllte blaue Punkt gibt (x₀,f(x₀)) an)

Analog heißt f im Punkt x₀ unterhalbstetig, wenn für jedes ε > 0 eine Umgebung U von x₀ existiert, so dass f(y) > f(x₀) − ε für alle y in U. Ist x ein Raum, in dem jede folgenstetige Funktion auch stetig ist, etwa ein metrischer Raum, so ist f genau dann unterhalbstetig in x, falls

$\liminf_{y\to x} f(y) \ge f(x)$.

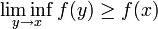f heißt unterhalbstetig auf einer Teilmenge M von X, wenn sie in jedem Punkt 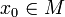$x_0\in M$ unterhalbstetig ist. Ist dabei M der ganze topologische Raum X, so heißt f unterhalbstetig.

Zusammenhang der beiden Halbstetigkeitsbegriffe: Die Funktion f ist genau dann oberhalbstetig in 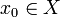$x_0\in X$ bzw. auf 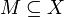$M\subseteq X$ wenn − f unterhalbstetig in 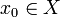$x_0\in X$ bzw. auf 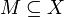$M\subseteq X$ ist.

Beispiele

Die Funktion f mit f(x) = 0 für x < 0 und f(x) = 1 für x ≥ 0 ist oberhalbstetig, aber nicht unterhalbstetig in x = 0. Denn geht man mit den Argumenten in negative Richtung von der 0 weg, dann springen die Funktionswerte plötzlich von 1 auf 0 runter, aber sie springen nicht nach oben, egal wohin man weggeht.

Die Gaußklammer ist oberhalbstetig, denn sie verhält sich an jeder ganzen Zahl so wie die eben beschriebene Funktion f.

Eigenschaften

Eine Funktion ist stetig in x genau dann, wenn sie dort halbstetig von oben und von unten ist.

Sind f und g zwei in x oberhalbstetige Funktionen, dann ist auch ihre Summe f + g in x oberhalbstetig. Sind beide Funktionen nichtnegativ in einer Umgebung von x, dann ist auch das Produkt fg in x oberhalbstetig. Die Multiplikation einer positiven oberhalbstetigen Funktion mit einer negativen reellen Zahl ergibt eine unterhalbstetige Funktion.

Ist D eine kompakte Menge (zum Beispiel ein abgeschlossenes Intervall [a,b] mit reellen Zahlen a < b) und 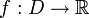$f: D \to \mathbb{R}$ oberhalbstetig, dann hat f ein Maximum auf D. Analoges gilt für eine unterhalbstetige Funktion und ihr Minimum.

Sind die Funktionen 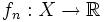$f_n: X \to \mathbb{R}$ (für alle n aus $\mathbb{N}$) unterhalbstetig und ihr Supremum

$f(x) := \sup \{f_n(x) : n \in \mathbb{N}\}$

kleiner als ∞ für jedes x in x, dann ist f unterhalbstetig. Selbst wenn alle f_n stetig sind, muss f aber nicht stetig sein.

Alternative Beschreibung

Durch eine geeignete Wahl einer Topologie auf $\mathbb{R}$ können oberhalbstetige und unterhalbstetige Funktionen als stetige Funktionen aufgefasst werden, und somit lassen sich einige der Eigenschaften direkt aus allgemeinen Aussagen aus der Topologie herleiten.

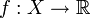$O_{&amp;amp;lt;}:=\{]-\infty,a[;a\in\mathbb{R}\cup\{+\infty\}\}$ ist eine Topologie auf $\mathbb{R}$. Sei (X,O) ein topologischer Raum. Eine Funktion $f:X\rightarrow\mathbb{R}$ ist genau dann oberhalbstetig, wenn f als Abbildung 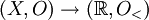$(X,O)\rightarrow (\mathbb{R},O_{&amp;amp;lt;})$ stetig ist.

Für unterhalbstetige Funktionen verwendet man analog die Topologie $O_{&amp;amp;gt;}:=\{]a,\infty[;a\in\mathbb{R}\cup\{-\infty\}\}$.