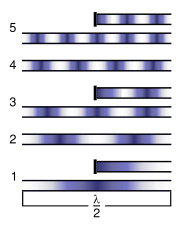
Obertöne

Die Artikel Teilton und Oberton überschneiden sich thematisch. Hilf mit, die Artikel besser voneinander abzugrenzen oder zu vereinigen. Beteilige dich dazu an der Diskussion über diese Überschneidungen. Bitte entferne diesen Baustein erst nach vollständiger Abarbeitung der Redundanz. Docbritzel 18:29, 18. Feb. 2008 (CET)

Ein Oberton ist ein ganzzahliges Vielfaches der Schwingung eines Grundtons. Grundton und Obertöne zusammen nennt man auch Teiltöne, Partialtöne oder Harmonische.

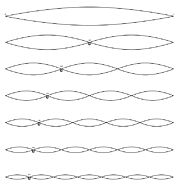Obertöne einer Saite

Die Nummer des Obertons ist immer um eins kleiner als die Nummer des Teiltons, bzw. des Partialtons oder der Harmonischen.

Grundlagen

Hörbeispiel: Der Grundton A1 (55 Hz) und die darauf aufbauende Obertonreihe bis einschließlich a3 (1.760 Hz), dargestellt an Sinustönen

Obertöne über dem C

Das menschliche Gehör nimmt periodische Schwingungen als Töne (im Sinne von musikalischen Tönen) wahr, wobei die Schwingungsperiode die wahrgenommene Tonhöhe bestimmt. Analysiert man das Frequenzspektrum periodischer Schwingungen (z. B. mit Hilfe der Fourier-Transformation), so besteht dieses aus

• einer Grundfrequenz (Grundton), die der Schwingungsperiode entspricht
• und Frequenzen, die ganzzahligen Vielfachen der Grundfrequenz entsprechen, den Obertönen.
  

Während der Grundton meistens die empfundene Tonhöhe des Tons bestimmt, bestimmen die Obertöne wesentlich die Klangfarbe dieses Tons.

Die genannten Schwingungsfrequenzen werden auch als Teiltöne des Klangs bezeichnet. Der erste Teilton ist die Grundfrequenz; der erste Oberton ist das Gleiche wie der zweite Teilton, der zweite Oberton der dritte Teilton usw.

Bei vielen Musikinstrumenten oder bei Vokalen der menschlichen Stimme besteht ein wesentlicher Teil des Klangs aus periodischen Schwingungen, die sich durch Grundton und Obertöne beschreiben lassen: zum Beispiel schwingende Saiten bei Saiteninstrumenten (Chordophone), schwingende Luftsäule bei Blasinstrumenten (Aerophone).

Daneben treten allerdings auch nicht-periodische Schwingungen auf, die ein eher breitbandiges Frequenzspektrum besitzen und sich nicht durch Grundton und Obertöne beschreiben lassen: z. B. Anschlag-Geräusche bei Saiteninstrumenten, Anblas-Geräusche bei Blasinstrumenten und Orgelpfeifen, Konsonanten bei der menschlichen Stimme.

In einer allgemeineren Darstellung bezeichnet man bei Schwingungen, die sich durch eine Reihe einzelner Frequenzen beschreiben lassen, alle Frequenzen, die oberhalb der Grundfrequenz liegen, als Obertöne, selbst wenn sie keine ganzzahligen Vielfachen der Grundfrequenz sind.

Obertöne und Klangfarbe

Obertöne der menschlichen Stimme

In der menschlichen Stimme schwingt, genau wie in den meisten klangerzeugenden physikalischen Systemen, ein komplexes Obertonspektrum mit. In der besonderen Gesangstechnik des Obertongesangs kann man diese hohen Frequenzen zum Dominieren bringen.

Der unterschiedliche Klang von Vokalen kommt durch deren spezifischen Obertonaufbau zustande. Durch die individuelle Größe und Form von Mund und Rachen werden manche Frequenzen durch Resonanz verstärkt, andere gedämpft. Die Frequenzbereiche, die jeweils verstärkt werden, nennt man auch Formanten.

Obertöne unterschiedlicher Instrumente

Wellen in offenen und gedackten Röhren. Die Wellenknoten sind blau.

Der spezifische Klang eines Instrumentes ergibt sich aus den folgenden Parametern:

• Welche Teiltöne überhaupt vorhanden sind (1., 2., 3., 5., 9., usw.)
• Wie laut diese Teiltöne im Verhältnis zueinander sind – Der erste muss nicht der lauteste sein
• Wie sich die Lautstärke der einzelnen Teiltöne ändert, während der Ton erklingt (Feinmodulation)
• Welche Nebengeräusche hinzukommen (Anschlaggeräusche, Blasgeräusche usw.)

Die Frequenzen der Obertöne hängen vom jeweiligen Klangerzeuger ab, es sind seine Eigenfrequenzen. Es gibt Instrumente mit harmonischen und solche mit nichtharmonischen Obertonreihen.

Bei Instrumenten mit harmonischen Obertonreihen sind die Frequenzen der Obertöne ganzzahlige Vielfache der Frequenz des Grundtons. Hierzu gehören die Chordophonen (Saiteninstrumente) und die Aerophone mit schwingender Luftsäule. In diesem Fall nennt man die Obertöne auch Harmonische. Das ist natürlich auch nur eine idealisierte Annahme; so besteht bei wirklichen (nicht unendlich dünnen) Saiten eine Inharmonizität. Gerade die sehr geringen Abweichungen von den idealen Harmonischen machen den Klang eines einzelnen Instrumentes unverwechselbar und lebendig.

Bei Instrumenten mit nichtharmonischen Obertonreihen stehen die Frequenzen der Teiltöne in komplizierten nicht ganzzahligen Verhältnissen zueinander. Die Obertöne der Membranophone mit runder Membran haben die Eigenfrequenzen einer Besselschen Differentialgleichung. Bei Idiophonen können sich je nach der Form des Klangkörpers ganz unterschiedliche Obertonreihen ergeben - bei den Stabspielen etwa sind es die Eigenfrequenzen der Biegeschwingung eines Balkens.

Künstlich aus Sinustönen hergestellte Obertonspektren nennt man synthetische Klänge (siehe Klangsynthese, Synthesizer). Eine reine Sägezahnschwingung zeichnet sich dadurch aus, dass sie zum Grundton alle seine Obertöne enthält, weshalb man sie zu den Zeiten der analog-elektronischen Musikinstrumente bevorzugt als Ausgangsschwingung einsetzte.

Folgende Instrumente haben einen besonders charakteristischen Teiltonaufbau:

• Streichinstrumente besitzen ein sehr reichhaltiges Teiltonspektrum. Es sind fast alle Teiltöne enthalten.
• Klarinetten betonen die Lautstärke der ungeraden Teiltöne.
• Beim Fagott ist der Grundton sehr viel schwächer als die ersten Harmonischen.
• Glocken betonen oftmals die Terzen sehr stark und beinhalten auch nicht-harmonische Obertöne.
• Stimmgabeln erzeugen fast nur den Grundton, daher ist deren Klang dem einer reinen Sinuskurve sehr ähnlich.

Wirkung der Obertöne: Brillanz und Dumpfheit

Der Anteil der Obertöne am Gesamtspektrum und die daraus resultierende Klangfarbe wird durch Worte wie Brillanz bzw. Dumpfheit, Helligkeit, Schärfe, Spitze beschrieben.

Im Allgemeinen klingen Töne umso brillanter, je mehr Obertöne sie haben, und umso dumpfer, je weniger sie haben.

Reine Töne ohne Obertöne, also Sinustöne, können praktisch gar nicht erzeugt werden. Näherungsweise können sie auf mechanischem Wege nur mit sehr geringen Schallpegeln erzeugt werden (Stimmgabel oder Hohlraumresonatoren, sehr sanft angeregt). Elektronisch ist die Erzeugung näherungsweise reiner Sinustöne problemlos möglich. Sie klingen bei tieferer Frequenz dumpf, breit und strömend, bestimmte Orgelregister kommen dem nahe. Bei höheren Frequenzen wird der Unterschied zu Klängen mit Obertönen geringer, weil diese Obertöne außerhalb des Hörbereichs liegen. Ein Beispiel der Situation für mittlere Frequenzen ist der 1000-Hertz-Ton des Fernsehtestbilds, wobei der Lautsprecher jedoch durch seine Verzerrungen schon wieder sein eigenes Obertonspektrum hinzufügt. Da die gesamte Energie nur in einem schmalen Frequenzbereich auftritt, können pegelstarke Sinustöne sehr unangenehm sein. Überhaupt sind Sinustöne ein Prüfstein für jeden Lautsprecher, da die Gefahr von elektrischer und mechanischer Überlastung einerseits sehr hoch ist, andererseits Verzerrungsprodukte mit hörbaren Pegeln sofort auffallen und mechanische Konstruktionsprobleme mit bisweilen schnarrenden oder fauchenden Resonanzen offengelegt werden.

In einem Mehrweg-Lautsprecher (Elektroakustik) ist in erster Linie der Hochtöner für die Brillanz, also für die Klanghelligkeit und die Klangfarbe der Wiedergabe zuständig.

Höhere Obertöne sind bei mechanischen Musikinstrumenten in der Regel leiser (pegelschwächer) als tiefere.

• Zum Einen werden bei mechanischen Tonerzeugern höhere Frequenzen nur wesentlich schwächer angeregt als tiefere (z. B. nimmt bei einer schwingenden Saite die Schwingungsamplitude der Obertöne mit steigender Frequenz ab)
• Zum anderen werden höhere Frequenzen in der Luft stärker gedämpft. Daher ist bei einer Beschallung über große Flächen die Brillanz der Wiedergabe meistens relativ schlecht.

Hörbarkeit von Obertönen

Auch im instrumentalen Bereich kann man Obertöne deutlich hörbar machen. Typische Instrumente hierfür sind z. B. das Didgeridoo, Fujara oder Klangschalen. Auf dem Klavier kann man Obertöne hörbar machen, indem man die Tasten eines Akkords aus der Obertonreihe sanft niederdrückt, ohne dass die Hämmer die Saite berühren, und dann den Grundton im Bassbereich kurz und stark anschlägt. Die Obertöne erzeugen nun eine Resonanz auf den ungedämpften Saiten der niedergedrückt gehaltenen Tasten, die man deutlich hören kann. Dieses wird auch von Komponisten in ihren Werken verwendet (z. B. Béla Bartók: Mikrokosmos, Band IV). Bei Saiteninstrumenten können Töne in der Tonhöhe von Obertönen durch Flageolett-Spielweise (siehe Flageolettton) erzeugt werden. Dabei wird die Saite mit der Greifhand nur leicht berührt anstatt sie auf das Griffbrett zu drücken.

In der Regel werden Obertöne nicht einzeln wahrgenommen, sondern sie ergeben den Klang eines Tons. Es gibt aber auch Menschen, die unter bestimmten Bedingungen Obertöne auch ohne jegliche Hilfe deutlich wahrnehmen können. Dieses gilt besonders bei sehr stabilen Tönen wie beispielsweise bei lang ausgehaltenen Tönen von Orgelpfeifen.

Die Gesangstechnik des Obertonsingens macht die Obertöne deutlich wahrnehmbar. Beispiele sind der Obertongesang mongolischer und tuvinischer Völker. Auch in der westlichen Musik gibt es seit Ende der sechziger Jahre wieder eine Belebung der Obertonkultur.

Untertonreihen

Theoretisch wird die Obertonreihe durch die zu ihr symmetrischen Untertonreihe, die durch Frequenzteilung entsteht, nach unten hin ergänzt. In der Natur gibt es eine solche Untertonreihe nicht (von Glocken- und Gong-Klängen abgesehen). Praktisch wurde sie beim Trautonium, beim Subharchord und beim Untertongesang umgesetzt.

Anwendungen

Die Orgel und ihre Register

Besonders wichtig ist die Obertonreihe auch bei der Orgel. Durch verschiedene Orgelregister, die jeweils einzelne Obertöne erzeugen (Aliquoten), lassen sich Klangfarben durch eine einfache Art Additive Synthese erzeugen. Bei Pfeifenorgeln ist nur ein „an“ oder „aus“ der Register möglich.

Bei der Hammond-Orgel können mit den neun Zugriegeln der Registerlagen (16', 8', 5¹/₃', 4', 2²/₃', 2', 1³/₅', 1¹/₃', 1') in jeweils neunstufiger Intensität der sinusförmigen Teiltöne durch Additive Synthese mehrere Millionen Klangfarben erzeugt werden. Bei der Hammond-Orgel sind allerdings nur die Oktaven (8', 4', 2', 1') harmonische Obertöne, die Quinten (5¹/₃', 2²/₃', 1¹/₃') und die Terz 1³/₅' sind hingegen näherungsweise gleichstufig gestimmt und damit unharmonische Obertöne und die von der Pfeifenorgel übernommenen Fußangaben somit nur Näherungswerte. Siehe hierzu Zugriegel und Fußlagen im Artikel Hammond-Orgel.

Residualtöne

Das menschliche Hörzentrum ist in der Lage, zu einem (auch nur teilweise) erklingenden Obertonspektrum die Grundfrequenz wahrzunehmen, auch wenn diese nicht erklingt. Diesen „hinzugefügten“ Grundton bezeichnet man auch als Residualton.

Musiktheorie und Kultur

Die Existenz von Obertönen wird seit langer Zeit zu einer wissenschaftlichen Erklärung und Begründung von Tonsystemen der Musik herangezogen. Ein ästhetisches System soll dabei also wissenschaftlich legitimiert werden, ja als naturnotwendig dargestellt werden, was an sich schon Zweifel aufkommen lässt. Die erste dieser Theorien wird Pythagoras zugerechnet, dieses war vor rund 2500 Jahren. Einen der letzten Versuche dieser Art findet man bei Hindemith in seiner Unterweisung im Tonsatz. Schon Pythagoras war aber klar, dass kein musikalisches Tonsystem konstruiert werden kann, das einerseits den Verhältnissen von ganzen Zahlen (den Obertönen, letztlich rationalen Zahlen) und andererseits der Forderung nach der Gleichwertigkeit der Tonschritte (dieses erfordert mathematisch geometrische Folgen, also irrationale Verhältnisse) Rechnung trägt. Zweifelsohne ist das moderne, westliche System mit 12 Tönen in gleichschwebender Stimmung ein guter Kompromiss, aber keine Lösung. Deswegen gibt es daneben eine Vielzahl von Stimmungen, die versuchen, die Rauhigkeiten auf andere Weise zu minimieren.

Zusätzlich muss festgestellt werden, dass die sog. natürlichen Obertöne" mit ihren ganzzahligen Verhältnissen sich nur in einer äußerst künstlich bereiteten Situation - nämlich in hochentwickelten Musikinstrumenten, die eindimensionale Schwingungen bevorzugt entwickeln - einstellen, und auch da nur in Näherung. Mechanische Klangerzeuger, wie sie jedes Kind mit Gummibändern zusammenbaut, zeigen, wie dieses im anderen Extrem -also schon eher "natürlich" - klingt. Nur elektronische Klangerzeuger erlauben es, ganzzahlige Verhältnisse in Perfektion zu erzeugen, worauf prompt dieser - nun der Musiktheorie nach ideale - Klangcharakter von Musikern negativ bewertet wird.

Mathematisch bleibt hinzuweisen, dass sinusförmige Schwingungen nur dann sinusförmig sind, wenn sie unendlich lange andauern und andauern werden. Die Sinusfunktion erstreckt sich beidseitig in die Unendlichkeit und ein Abschneiden der Dauer führt mathematisch zu etwas Anderem, dem Wellikel, einer zeitlich begrenzten Welle. Diese besitzt aber keine scharf voneinander abgegrenzten Obertöne mehr, sondern ein verschmiertes Frequenzband. In psychoakustischer Konsequenz ergeben sich Knacker beim Abschneiden von langandauernden, statischen Sinustönen oder Sinustongemischen. Bei kurzandauernden Vorgängen solcher Art - wie sie bei allen Instrumenten auftreten, bei denen nicht stets Energie nachgereicht wird, also vor allem den Zupf- und Schlaginstrumenten (auch dem Klavier) - ist die Grundvoraussetzung des Dauertones noch nicht einmal mehr in Näherung gegeben.

In der Kultur der Ingenieurwissenschaften ging man meistens von der Situation aus, dass Vorgänge langandauernd und langsam veränderlich sind (bei der Modulation eines Radiosenders ist dieses der Fall). Nur dann machen die Fouriertransformation und die daraus implizit im Artikel folgenden Begriffe einen Sinn. Erst in den letzten Dekaden hat sich die Einsicht durchgesetzt, dass bei schnell veränderlichen und kurz andauernden Vorgängen die Wavelet-Transformation Anwendung finden muss, worauf Begriffe wie etwa Frequenz neu gedeutet werden müssen.

Musik beinhaltet wesentlich solche Vorgänge. Insofern ist auch aus dieser Sicht Kritik an überkommenen Vorstellungen zu üben.

Musikdidaktik

Zuerst hat sich Johann Bernhard Logier (1777-1846) die Obertonreihe für didaktische Zwecke (Lehre der Begleitung, Generalbass, Harmonie und Melodie sowie Kompositionslehre) zu Nutze gemacht. Seine Lehre von den "harmonisch mitklingenden" Tönen war zu seinen Lebzeiten stets umstritten; seine didaktisch hoch reflektierten Werke mit ihren einfachen, aufeinander aufbauenden Grundregeln dürfen jedoch als Anfang der modernen, noch heute gültigen Musiktheorie gelten. (Vgl. vor allem: J. B. Logier, System der Musik-Wissenschaft und der praktischen Composition mit Inbegriff dessen, was gewöhnlich unter dem Ausdrucke General-Bass verstanden wird, Berlin 1827. S. 11: Quintenzirkel, Generalbass: S. 15ff., ab S. 53 beginnt die Lehre der Obertöne.)

Literatur

• John R. Pierce, Klang. Musik mit den Ohren der Physik, Spektrum, ISBN 3-8274-0544-0

Siehe auch

• Vokaldreieck, Vokaltrapez, Flageolettton, Obertongesang
• Psychoakustik, Differenzton
• Stimmung (Musik)
• Fourieranalyse, Schwingung, Rechteckschwingung, Kippschwingung

Weblinks

• Wie die Obertöne entstehen
• Die Partialschwingungen einer Trommel in animierten Graphiken
• Harmonische, Partialtöne, Teiltöne und Obertöne
• Die Teiltondichte und die Teiltonreihe
• Unterscheide Obertöne von Harmonischen, Partialtönen und Teiltönen
• Die Frequenzverhältnisse, die sich für Intervalle aus der Obertonreihe ergeben
• Hörproben der gesungenen Obertonreihe bzw. Naturtonreihe
• Obertonspektren verschiedener Instrumente
• Obertongesang
• Berechnung der Obertöne aus der Grundfrequenz in Hz