Orthogon

Rechteck

ist Spezialfall von

Viereck Trapez Parallelogramm

umfasst als Spezialfälle

Quadrat

In der Geometrie ist ein Rechteck (ein Orthogon) ein ebenes Viereck, dessen Innenwinkel alle rechte Winkel sind.

Rechteck mit Länge a, Breite b und Diagonale d

Für jedes Rechteck gilt:

• Gegenüberliegende Seiten sind gleich lang und parallel.
• Die beiden Diagonalen sind gleich lang und halbieren einander.
• Es besitzt einen Umkreis und ist daher ein Sehnenviereck. Der Schnittpunkt der Diagonalen ist der Umkreismittelpunkt.
• Es ist achsensymmetrisch bezüglich der Mittelsenkrechten (Seitensymmetralen) der Rechtecksseiten. Die beiden Symmetrieachsen stehen also senkrecht aufeinander.
• Es ist punktsymmetrisch (zweizählig symmetrisch) bezüglich des Diagonalenschnittpunkts.

Beim Rechteck handelt es sich um einen Spezialfall des Parallelogramms (gleichwinkeliges Parallelogramm) und damit auch des Trapezes.

Ein Sonderfall des Rechtecks ist das Quadrat, bei dem alle Seiten gleich lang sind (gleichseitiges Rechteck).

Formeln zum Rechteck
Flächeninhalt	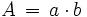$A \, = \, a \cdot b$
Umfang	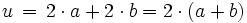$u \, = \, 2 \cdot a + 2 \cdot b = 2 \cdot (a + b)$
Diagonalenlänge	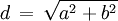$d \, = \, \sqrt{a^2+b^2}$
Umkreisradius	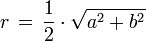$r \, = \, \frac{1}{2} \cdot \sqrt{a^2+b^2}$
Seitenlängen	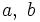$a,\;b$

Die Formel für die Diagonalenlänge beruht auf dem Satz des Pythagoras. Der Umkreisradius ergibt sich durch Halbierung der Diagonalenlänge.

Ein Rechteck heißt perfekt, falls man es mit Quadraten lückenlos und überschneidungsfrei überdecken kann, wobei alle Quadrate unterschiedlich groß sind. Es ist nicht einfach, eine solche Zerlegung zu finden. Eine solche Zerlegung eines Rechtecks in 9 Quadrate wurde 1925 von Morón gefunden. Sie besteht aus den Quadraten mit den Seitenlängen: 1, 4, 7, 8, 9, 10, 14, 15, 18.

Rechtecke mit der Eigenschaft 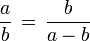$\frac{a}{b} \, = \, \frac{b}{a - b}$ nennt man "Goldene Rechtecke". Siehe auch goldener Schnitt.

Siehe auch

• Querschnittsfläche

Weblinks

• Rechteck Animierte Lernsequenz - Konstruktion, Umfang, Flächeninhalt

Konvexe Vierecke

Quadrat | Rechteck | Raute | Parallelogramm | Drachenviereck | Trapez | Sehnenviereck | Tangentenviereck