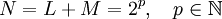- Overlap-Add-Verfahren
-
Das Overlap-Add-Verfahren ist ein Verfahren zur Schnellen Faltung und wird in der digitalen Signalverarbeitung eingesetzt. Dabei wird eine Eingangsfolge in einander überlappende Teilfolgen zerlegt und die Überlappungsbereiche, im Gegensatz zum Overlap-Save-Verfahren, aufaddiert. Das Ziel dieses Verfahrens ist die zirkulare Faltungsoperation der zur schnellen Faltung eingesetzten schnellen Fourier-Transformation in die aperiodische Faltungsoperation überzuführen.
In den Anwendungen wird das Overlap-Add-Verfahren zur effizienten Implementierung von FIR-Filtern höherer Ordnung verwendet. Das Overlap-Add-Verfahren hat dabei im Gegensatz zur direkten Implementierung der aperiodischen Faltungsoperation in digitalen Signalprozessoren (DSP) den Vorteil Ressourcen wie Speicher oder Rechenzeit zu sparen.
Inhaltsverzeichnis
Verfahren
Die direkte Ausführung der aperiodischen Faltungsoperation zwischen einer beliebig langen Eingangsfolge x[n] und der Impulsantwort h[n] der Länge M ergibt die Ausgangsfolge y[n]:
wobei h[m] außerhalb des Intervalls [1, M] gleich 0 gesetzt ist. Die Idee des Verfahrens beruht darauf, Teilfolgen mit der Länge L der Eingangsfolge zu bilden, welche mit dem Index k zur Unterscheidung bezeichnet sind. Der Teilfolgen werden mit Nullen aufgefüllt, was auch als Zero-Padding bezeichnet wird:
Die Eingangsfolge x[n] besteht aus der Summe der Teilfolgen xk[n]
x[n] = ∑ xk[n − kL] k womit die Ausgangsfolge y[n] als Summe einzelner Faltungen dargestellt werden kann:
Die Ausgangsteilfolgen
sind ausserhalb des Intervalls [1,L+M-1] Null. Für jeden Wert des Parameters N welcher grösser-gleich als L+M-1 gewählt sein muss, ergibt sich die zirkulare Faltungsoperation der Ausgangsfolge. Die einzelnen Ausgabefolgen yk[k] überlappten sich in den Intervallen [k(L+1),k(L+M)] und durch die Summation wird die Ausgabefolge y[k] gebildet.
Der Vorteil besteht darin, dass die zirkulare Faltungsoperation zur Bildung der Teilfolgen yk effizient in Form der schnellen Fourier-Transformation (FFT) bzw. der inversen schnellen Fourier-Transformation (IFFT) nach folgender Form implementiert werden kann:
Je nach verwendeten FFT-Algorithmus ist es sinnvoll, die konkrete Blocklänge N zur Berechnung der zirkularen Teilfaltungen abzustimmen. Bei Verwendung des FFT-Algorithmus nach Cooley und Tukey (Radix-2-Algorithmus) ist es günstig die Blocklänge als Zweierpotenz zu wählen:
Pseudocode
(Overlap-Add-Verfahren) In Abhängigkeit des FFT-Algorithmus N und L wählen. H = FFT(h,N) i = 1 while i <= Nx il = min(i+L-1,Nx) yt = IFFT( FFT(x(i:il),N) * H, N) k = min(i+N-1,Nx) y(i:k) = y(i:k) + yt (die überlappenden Bereiche addieren) i = i+L endLiteratur
- Karl-Dirk Kammeyer, Kristian Kroschel: Digitale Signalverarbeitung. 6. Auflage. Teubner, 2006, ISBN 3-8351-0072-6.
- Alan V. Oppenheim, Ronald W. Schafer: Zeitdiskrete Signalverarbeitung. 3. Auflage. R.Oldenbourg, 1999, ISBN 3-486-24145-1.
Weblinks
Wikimedia Foundation.


![y[n] = x[n] * h[n] \ \stackrel{\mathrm{def}}{=} \ \sum_{m=-\infty}^{\infty} h[m] \cdot x[n-m]
= \sum_{m=1}^{M} h[m] \cdot x[n-m]](/pictures/dewiki/51/3b2a9ba238dd316616223438b67e4cef.png)
![x_k[n] \ \stackrel{\mathrm{def}}{=}
\begin{cases}
x[n+kL] &amp;amp; n=1,2,\ldots,L\\0
&amp;amp; \textrm{ansonsten}
\end{cases}](/pictures/dewiki/51/3921642956a098cd7d14e138f9fbf809.png)
![\begin{align}
y[n] = \left(\sum_{k} x_k[n-kL]\right) * h[n] &amp;amp;= \sum_{k} \left(x_k[n-kL]* h[n]\right)\\
&amp;amp;= \sum_{k} y_k[n-kL]
\end{align}](/pictures/dewiki/102/f5ec5af0e2a7a86ee8732ed16436bf43.png)
![y_k[n] \ \stackrel{\mathrm{def}}{=} \ x_k[n]*h[n]](/pictures/dewiki/52/419110fb955e0d15a1557ac940b61ccb.png)
![y_k[n] = \textrm{IFFT}\left(\textrm{FFT}\left(x_k[n]\right)\cdot\textrm{FFT}\left(h[n]\right)\right)](/pictures/dewiki/100/d3021081f6ca5241ce4df6e288fb74c5.png)