- P-Exponent
-
Im mathematischen Teilgebiet der Bewertungstheorie geht es um Verallgemeinerungen der Frage, durch welche Potenz einer festen Primzahl eine natürliche Zahl teilbar ist.
Inhaltsverzeichnis
p-Bewertung
Es sei p eine Primzahl.
Die p-Bewertung (auch: die p-adische Bewertung oder der p-Exponent) vp(n) einer natürlichen oder ganzen Zahl n ist die größte Zahl k, so dass n noch durch pk teilbar ist. Die p-Bewertung gibt an, wie oft eine Primzahl p in der Primfaktorzerlegung einer natürlichen oder ganzen Zahl vorkommt.
Die p-Bewertung einer natürlichen Zahl n ist der Exponent der Primzahl p in der Primfaktorzerlegung von n. Ist
so ist
Tritt eine Primzahl p nicht in der Primfaktorzerlegung von n auf, dann ist vp(n) = 0.
Man setzt
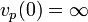 , weil jede Potenz jeder Primzahl die 0 teilt.
, weil jede Potenz jeder Primzahl die 0 teilt.Die p-Bewertung einer ganzen Zahl ist die ihres Betrags.
Die p-Bewertung einer rationalen Zahl ist die Differenz der p-Bewertungen des Zählers und des Nenners: Für eine rationale Zahl
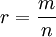 mit
mit 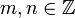 ist also
ist also- vp(r) = vp(m) − vp(n).
Geht p nur im Nenner des (vollständig gekürzten) Bruchs m / n auf, ist vp(r) also eine negative Zahl.
Die p-Bewertung rationaler Zahlen spielt eine wichtige Rolle bei einer Konstruktionsart der p-adischen Zahlen: die Funktion
bildet auf den rationalen Zahlen einen nichtarchimedischen Betrag.
p-ganze und S-ganze Zahlen
Eine p-ganze Zahl (auch "p-adisch ganze Zahl" oder "für p ganze Zahl") ist eine rationale Zahl, die nichtnegative p-Bewertung hat, d.h. bei der in einer vollständig gekürzten Bruchdarstellung der Nenner nicht durch p teilbar ist. Rationale Zahlen, die nicht p-ganz sind, werden manchmal auch "p-gebrochen" genannt.
Die Menge aller p-ganzen Zahlen ist ein Unterring von
 , der
, der 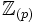 geschrieben wird.
geschrieben wird. 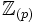 ist ein diskreter Bewertungsring, insbesondere gibt es bis auf Assoziierte genau ein irreduzibles Element, nämlich p.
ist ein diskreter Bewertungsring, insbesondere gibt es bis auf Assoziierte genau ein irreduzibles Element, nämlich p.Ist allgemeiner S eine Menge von Primzahlen, so ist eine S-ganze Zahl eine rationale Zahl, die p-ganz für jedes
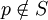 ist (!), d.h. bei der in einer vollständig gekürzten Bruchdarstellung der Nenner nur durch Primzahlen aus S teilbar ist. Die Menge der S-ganzen Zahlen bildet einen Unterring
ist (!), d.h. bei der in einer vollständig gekürzten Bruchdarstellung der Nenner nur durch Primzahlen aus S teilbar ist. Die Menge der S-ganzen Zahlen bildet einen Unterring 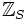 von
von  . Beispielsweise ist für
. Beispielsweise ist für 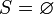 also
also 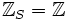 , für
, für 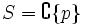 ist
ist 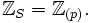
Diskrete Bewertungen
Es sei K ein Körper. Dann heißt eine surjektive Funktion
eine diskrete Bewertung, wenn die folgenden Eigenschaften erfüllt sind:
- v(ab) = v(a) + v(b)
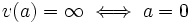
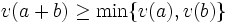
für alle
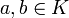 . K zusammen mit v heißt diskret bewerteter Körper.
. K zusammen mit v heißt diskret bewerteter Körper.Beispiele
- die p-Bewertung auf den rationalen Zahlen für eine Primzahl p
- die Nullstellen- bzw. Polordnung meromorpher Funktionen in einem festen Punkt
Diskrete Bewertungen und diskrete Bewertungsringe
Die Teilmenge
bildet einen Unterring von K, den Bewertungsring von v. Er ist ein diskreter Bewertungsring, und ist umgekehrt
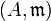 ein diskreter Bewertungsring, so ist durch
ein diskreter Bewertungsring, so ist durcheine diskrete Bewertung auf dem Quotientenkörper von A definiert.
Diskrete Bewertungsringe und diskret bewertete Körper entsprechen einander.
Allgemeine Bewertungen
Ist G eine totalgeordnete abelsche Gruppe und K ein (kommutativer) Körper, so ist eine Abbildung
eine Bewertung, wenn die folgenden Eigenschaften erfüllt sind:
- v(ab) = v(a) + v(b)
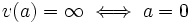
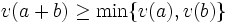
für alle
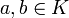 .
.K heißt dann auch ein bewerteter Körper mit Wertegruppe
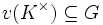 .
.Bewertungen und Bewertungsringe
Ein Integritätsbereich A heißt Bewertungsring, wenn er die folgende Eigenschaft hat:
- Für jedes Element x des Quotientenkörpers von A gilt
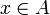 oder
oder 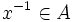 .
.
Ist A ein Bewertungsring mit Quotientenkörper K, so kann man eine Bewertung auf K mit Wertegruppe
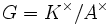 definieren:
definieren:dabei bezeichnet [x] das Bild von x in
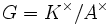 ; die Ordnung auf G ist definiert durch
; die Ordnung auf G ist definiert durch![[x]\geq[y]\iff xy^{-1}\in A](/pictures/dewiki/99/ce779dc6f2fd078c2cd8ad519d519d0b.png) für
für 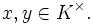
Ist umgekehrt K ein bewerteter Körper mit Bewertung v, so ist
ein Bewertungsring, der dann auch der Bewertungsring zur Bewertung v genannt wird. Die Gruppe
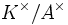 ist kanonisch isomorph zur Wertegruppe von v.
ist kanonisch isomorph zur Wertegruppe von v.Für einen Körper K gibt es also eine bijektive Beziehung zwischen Isomorphieklassen von Bewertungen auf K und Bewertungsringen, die in K enthalten sind.
Wikimedia Foundation.

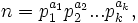
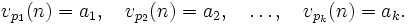
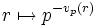
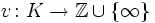
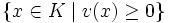
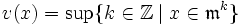
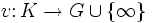
![v\colon K\to G\cup\{\infty\},\quad v(x)=\left\{\begin{matrix}\infty&x=0\\{}[x]&x\in K^\times;\end{matrix}\right.](/pictures/dewiki/48/06b7fddd147fac1ef5b8441969631bcb.png)