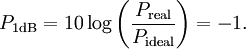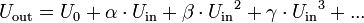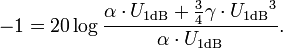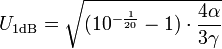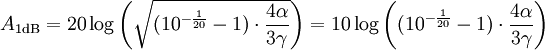P1dB

Der Kompressionspunkt dient zur quantitativen Beschreibung des nichtlinearen Verhalten eines aktiven Elements (etwa eines Verstärkers) z. B. bei Audiokomponenten oder in der Hochfrequenztechnik. Er gibt die größte Amplitude des Eingangssignals an, bei der die durch Nichtlinearität hervorgerufenen Verzerrungen ein vorgegebenes Maß noch nicht überschreiten.

Ursache des nichtlinearen Verhaltens ist die Sättigung, die bei jedem verstärkenden Bauelement (Transistor, Elektronenröhre) oberhalb einer bestimmten Eingangsamplitude eintritt. Die Bezeichnung Kompressionspunkt weist darauf hin, dass die Sättigung immer zu einem gegenüber dem linearen Fall verkleinerten, also "komprimierten" (zusammengedrückten) Ausgangssignal führt.

Definition

Der 1-dB-Kompressionspunkt, oft als P1dB bezeichnet, ist derjenige Wert der Eingangsamplitude, bei dem die Amplitude des Ausgangssignals auf der Grundfrequenz um 1 Dezibel von der idealen linear extrapolierten Kennlinie des Bauteils abweicht

$P_{1\mathrm{dB}}=10\log\left({\frac{P_\mathrm{real}}{P_\mathrm{ideal}}}\right)=-1.$

(P_real und P_ideal sind hier lineare Größen.)

In Datenblättern wird der P1dB als Eingangsleistung in dBm angegeben. Neben dem 1-dB-Kompressionspunkt kann man auch jeden beliebigen andern Kompressionspunkt, z. B. P3dB für eine Abweichung von 3dB, definieren.

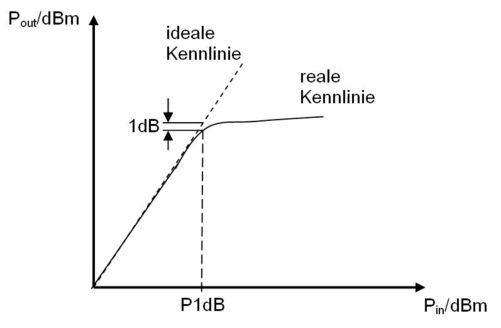
Schematische Darstellung

Berechnung der Amplitude

Beispiel für einen Verstärker:

Die Kennlinie eines nicht linearen Verstärkers lässt sich durch eine Taylor-Reihe

$U_\mathrm{out}=U_0+\alpha\cdot U_\mathrm{in}+\beta\cdot {U_\mathrm{in}}^2+\gamma\cdot {U_\mathrm{in}}^3+...$

beschreiben.

Im 1-dB-Kompressionspunkt gilt

$-1=20\log\frac{\alpha\cdot U_\mathrm{1dB}+\frac{3}{4}\gamma\cdot {U_\mathrm{1dB}}^3}{\alpha\cdot U_\mathrm{1dB}}.$

U_1dB ist die Amplitude im 1dB-Kompressionspunkt

Umgestellt ergibt sich:

$U_\mathrm{1dB}=\sqrt{(10^{-\frac{1}{20}}-1)\cdot\frac{4\alpha}{3\gamma}}$

bzw. logarithmisch:

$A_\mathrm{1dB}=20\log\left(\sqrt{(10^{-\frac{1}{20}}-1)\cdot\frac{4\alpha}{3\gamma}}\right)=10\log\left({(10^{-\frac{1}{20}}-1)\cdot\frac{4\alpha}{3\gamma}}\right)$

siehe auch

• Intercept Point

Weblinks

• Beschreibung des 1-dB Kompressionspunktes auf Seite 7
• Beschreibung des 1-dB Kompressionspunktes auf Seite 9
• Beschreibung des 1-dB Kompressionspunktes auf Seite 37