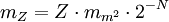Papiergrößen

	DIN EN ISO 216
Bereich	Bürowesen
Regelt	Schreibpapier und bestimmte Gruppen von Drucksachen - Endformate - A- und B-Reihen und Kennzeichnung der Maschinenlaufrichtung
Kurzbeschreibung	ISO-Papierformate
Letzte Ausgabe	12.2007
ISO	216

Die Standardgrößen für Papierformate (siehe Papier) in Deutschland sind die vom Deutschen Institut für Normung (DIN) 1922 in der DIN-Norm DIN 476 festgelegten Formate. Entwickelt wurde der Standard vom Berliner Ingenieur Dr. Walter Porstmann. Der Entwurf ähnelt den in Vergessenheit geratenen Entwürfen aus der Zeit der Französischen Revolution.

Die deutsche Norm diente als Grundlage für das internationale Äquivalent EN ISO 216, das wiederum in fast allen Ländern adaptiert worden ist. Unterschiede gibt es meist nur in den erlaubten Toleranzen. Parallel existieren, etwa in den USA, Kanada und Mexiko, auch traditionelle, meist weniger systematisch und praktisch aufgebaute Systeme.

In der Papier- und Druckindustrie erfolgt die Formatangabe grundsätzlich mit Breite × Höhe, und zwar immer in dieser Reihenfolge. Deshalb lässt sich daraus schließen, ob es sich um ein Hoch- oder ein Querformat handelt.

Internationale Papierformate (ISO/DIN)

Aufteilung eines A0-Bogens. Die Formate ergeben sich jeweils durch Halbierung des nächstgrößeren.

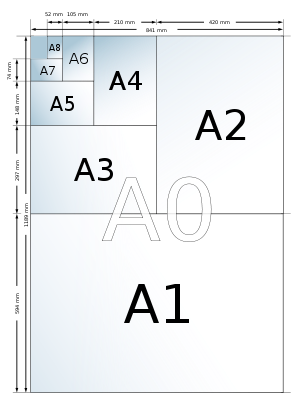
Das Referenzformat der A-Reihe ist A0, dessen Flächeninhalt einen Quadratmeter beträgt.

Das Verhältnis der beiden Seitenlängen eines Blattes im DIN-Format beträgt 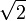$\sqrt{2}$ (etwa 1 : 1,414) mit Abrundung auf ganze Millimeter. Dadurch ist sichergestellt, dass bei Halbierung des Blattes entlang der längeren Seite wieder ein Blatt im DIN-A-Format (mit um 1 erhöhter Nummerierung) entsteht. Entgegen einer verbreiteten Annahme entspricht dieses Maß nicht dem Goldenen Schnitt 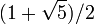$(1 + \sqrt{5})/2$ (etwa 1 : 1,618), das ist das historische Format Oktav.

√2 entspricht dem Verhältnis der Diagonalen eines Quadrates zu dessen Seitenlänge. Damit kann man die lange Seite l eines Blattes im DIN-Format als die Diagonale eines Quadrates auffassen, das dieselbe Seitenlänge hat wie die kurze Seite s des DIN-Formates.

$l \, = \, s \cdot \sqrt{2}$

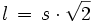
Bei der Berechnung der Seitenlängen wird auf ganze Millimeter abgerundet.

Man kann das Seitenverhältnis von √2 wie folgt herleiten: Gegeben ist, dass das Seitenverhältnis bei den DIN-Formaten stets gleich ist und dass man durch Verdopplung der kurzen Seite das Format mit der nächstkleineren Nummer erhält (z. B. aus A4 erhält man A3). Wenn man das Seitenverhältnis mit c und die kurze Seite mit s bezeichnet, ergibt sich daraus das Format s × c·s und das nächstgrößere Format (c·s × 2·s). Mit der Bedingung, dass das Seitenverhältnis auch beim großen Format gleich c sein muss, folgt für c:

$\frac{2\cdot s}{c\cdot s} = \frac{c\cdot s}{s} \ \Leftrightarrow \ 2 = c^2 \ \Rightarrow \ c = \sqrt{2}$

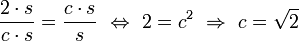
Die praktische Bedeutung des Seitenverhältnisses von √2 besteht darin, dass bei Halbieren eines solchen Blattes zwei Blätter im gleichen Seitenverhältnis entstehen; die Blätter sind somit geometrisch einander ähnlich. Die Idee zu einem solcherart teilbaren Papierformat hatte vermutlich zuerst Georg Christoph Lichtenberg. ^[1]

Dadurch ergeben sich die einzelnen Größen einer Reihe jeweils durch Verdoppeln der kleineren bzw. Halbieren der größeren Seitenlänge, so dass sich die Fläche (Höhe mal Breite) jeweils um den Faktor Zwei ändert. Nützlich ist das z. B. für Vergrößerungen und Verkleinerungen beim Fotokopieren (Skalierungsfaktor 141 % [√2] bzw. 70,7 % [√½]). Mit diesen Vorgaben lässt sich die Masse m_Z einer bekannten Anzahl Z Seiten eines Formats A_N näherungsweise berechnen, wenn das Quadratmetergewicht m_m² bekannt ist:

$m_Z = Z \cdot m_{m^{2}} \cdot 2^{-N}$

Das bedeutet z. B., dass ein DIN-A4-Blatt Standardbriefpapier (80 g/m²) eine Masse von fünf Gramm hat.

Die Höhen und Breiten und damit auch die Flächen der Formate der B-Serie errechnen sich aus dem geometrischen Mittel der Werte des entsprechenden und des nächstgrößeren A-Formats. Aus A0 (841 mm × 1189 mm) und 2A0 (1189 mm × 1682 mm) ergibt sich für B0:

B0 = √(841 mm · 1189 mm) × √(1189 mm · 1682 mm) = 1000 mm × 1414 mm.

Die Abmessungen der C-Serie ergeben sich wiederum aus dem geometrischen Mittel der A- und B-Formate gleicher Nummer, also:

C0 = √(841 mm · 1000 mm) × √(1189 mm · 1414 mm) = 917 mm × 1297 mm.

Die Abmessungen der D-Serie ergeben sich aus dem geometrischen Mittel der Werte des entsprechenden A-Formates und des nächstkleineren B-Formats. Aus A0 (841 mm × 1189 mm) und B1 (707 mm × 1000 mm) ergibt sich für D0:

D0 = √(841 mm · 707 mm) × √(1189 mm · 1000 mm) = 771 mm × 1091 mm.

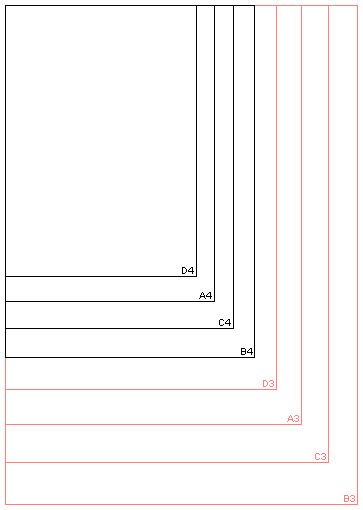
B-Formate sind immer größer als A-Formate mit gleicher Nummer, C-Formate liegen dazwischen und D-Formate sind am kleinsten.

Wenn wir zur Abkürzung $k=\sqrt[8]{2} \approx 1{,}0905$ setzen, ergibt sich in Formeln ausgedrückt die folgende einfache Übersicht (Angaben in Metern, ohne Rundung), absteigend nach Größe sortiert:

B0 = k⁰ × k⁴

C0 = k⁻¹ × k³

A0 = k⁻² × k²

D0 = k⁻³ × k¹

B1 = k⁻⁴ × k⁰

C1 = k⁻⁵ × k⁻¹

A1 = k⁻⁶ × k⁻²

D1 = k⁻⁷ × k⁻³

B2 = k⁻⁸ × k⁻⁴

usw.

Übersicht

Vergleich der DIN-Formate der Reihen A bis D
(ein Pixel entspricht einem Millimeter)

Benennung und Größe in Millimeter. Die Toleranz beträgt bei Maßen bis 150 mm ±1,5 mm, bei Maßen bis 600 mm ±2 mm und darüber ±3 mm. Die Übergrößen 2A0 und 4A0 gibt es nur in der DIN-, nicht in der ISO-Norm. Für „…“ ist der betreffende Buchstabe der Reihe einzusetzen, z. B. 4A0 = 1682 × 2378 oder B3 = 353 × 500.

ISO/DIN-Reihen A bis D (mm × mm)

	A	B	C	D
4…0	1682 × 2378
2…0	1189 × 1682	1414 × 2000
…0	841 × 1189	1000 × 1414	917 × 1297	771 × 1091
…1	594 × 841	707 × 1000	648 × 917	545 × 771
…2	420 × 594	500 × 707	458 × 648	385 × 545
…3	297 × 420	353 × 500	324 × 458	272 × 385
…4	210 × 297	250 × 353	229 × 324	192 × 272
…5	148 × 210	176 × 250	162 × 229	136 × 192
…6	105 × 148	125 × 176	114 × 162	96 × 136
…7	74 × 105	88 × 125	81 × 114	68 × 96
…8	52 × 74	62 × 88	57 × 81
…9	37 × 52	44 × 62	40 × 57
…10	26 × 37	31 × 44	28 × 40

• A0 Vierfachbogen
• A1 Doppelbogen
• A2 Bogen
• A3 Halbbogen
• A4 Viertelbogen (Briefbogen)
• A5 Blatt
• A6 Halbblatt (Postkarte)
• A7 Viertelblatt
• A8 Achtelblatt

Abgeleitete Formate

Aus der A-Reihe werden die Streifen-Formate durch Teilung abgeleitet.

1⁄4 A3

105 mm × 297 mm

1⁄3 A4

99 mm × 210 mm

1⁄4 A4

74 mm × 210 mm

1⁄8 A4

37 mm × 210 mm

1⁄3 A5

70 mm × 148 mm

1⁄6 DIN

200 mm × 210 mm (eigentlich nach DIN 198: 198 mm × 210 mm)

Weitere Formate für Briefumschläge:

DL-Umschlag (DIN lang)

110 mm × 220 mm – vgl. ¹⁄₃ A4

C6/C5-Umschlag

114 mm × 229 mm – aus der C-Reihe abgeleitet, etwas größer als DL, fasst größere Blattanzahl

Anwendungen

A0, A1	Technische Zeichnungen, Fahrpläne, Landkarten, Druckbogen, Poster, Filmplakate
A1, A2	Flipcharts, Geschenkpapier, Filmplakate, Fahrpläne, Kalender, Zeitungen
A2, A3	Zeichnungen, Diagramme, große Tabellen, Kalender, Filmplakate
B4, A3	Zeitungen, Taschentücher, Noten
A4	Briefpapier, Formulare, Hefte, Zeitschriften
A5	Notizblöcke, Schulhefte, Prospekte
D5	DVD-Hüllen
A5, A6, A7, A8	Karteikarten, selten auch A4 und A9
A6	Flyer, Postkarten, Taschenbücher, Überweisungsträger
B5, A5, B6, A6, A4	Bücher (Buchformat)
A7	Flugblätter, Taschenkalender, Personalausweis (ID-2)
B7	Reisepass (ID-3)
B8, A8	Spielkarten, Visitenkarten, Etiketten
C4, C5, C6, B4	Umschläge, (Kontoauszüge meist C6)

Überformate

Da beim Zuschneiden und Falten Verluste auftreten, wurden die Überformate RA und SRA geschaffen. Das R steht für „Rohformat“, S für „sekundäres“. RA0 hat prinzipiell eine Fläche von 1,05 m², SRA0 1,15 m², Breite und Höhe sind aber auf den ganzen Zentimeter gerundet.

ISO/DIN-Reihen RA und SRA (in Millimetern)

	RA-	SRA-
0	860 × 1220	900 × 1280
1	610 × 860	640 × 900
2	430 × 610	450 × 640
3	305 × 430	320 × 450
4	215 × 305	225 × 320

Unter der inoffiziellen Bezeichnung A4+ (A4 plus) existiert ferner ein auf dem DIN-A4-Format basierendes Überformat, das beim Einsatz in Tintenstrahl- und Laserdruckern Verwendung findet. Es wird für Endkunden speziell von Druckerherstellern angeboten. Durch die fehlende Normierung dieses Überformates existieren verschiedene Formate. So existieren auf DIN-A4 basierende Formate mit einer einheitlichen Beschnittzugabe von jeweils drei Millimetern pro Seite (216 mm × 303 mm) oder randlos bedruckbare Formate mit Abrisskanten. Einige (amerikanische) Anbieter spezifizieren das Format A4+ auch mit dem Maß 9½ Zoll × 13 Zoll (241 mm × 330 mm). Im Foto- und Werbedruck existiert auch das inoffizielle Überformat A3+ (A3 plus), auch unter Super A3 oder Super B bekannt, auch hier gibt es kein festgelegtes einheitliches Maß. Die Abmessungen sind meist so gewählt, dass auf einem Drucker des Papier-Herstellers eine A3-Seite randlos ausgedruckt werden kann.

Andere Formate

Außerdem gibt und gab es natürlich andere Systeme, beispielsweise bei Zeitungen. Manche alte Systeme haben sich zumindest in Teilen bis heute erhalten.

Maschinenformate

Für die Verarbeitung in Druckmaschinen gibt es einen Industriestandard, der folgende maximalen Papiergrößen umfasst.

Maschinenformate (in cm)

Formatklasse	Abmessungen	Formatklasse
00	35 × 50
01	46 × 64
0b	52 × 72	Kleinformat
1	56 × 83
2c	64 × 91
2	61 × 86
3	65 × 96
3b	72 × 102	Mittelformat
4	78 × 112
5	89 × 126
6	102 × 142
7	112 × 162
7b	120 × 162	Großformat
8	130 × 185
9	150 × 205	Supergroßformat
10	162 × 224

Verpackungsbogen

Im Verpackungsbereich kommen Formate zum Einsatz, die sich vom Ballenformat (75 cm × 100 cm) ableiten. Diese Formate beschränken sich nicht auf Papierbögen, sondern werden auch bei anderen Zuschnitten, z. B. aus Folie, verwendet. Ein Folgeformat entsteht jeweils durch Halbierung der langen Seite.

Verpackungsbogen

Kennung	Gebräuchlicher Name	Abmessungen (mm × mm)	Verwendungsbeispiele
1/1	Ganzer Bogen	750 × 1000	Verpackungspapiere, Stopfpapier
1/2	Halber Bogen	500 × 750	Brotseidenpapier, Bäckereipapiere
1/4	Viertelbogen	375 × 500	Frischhaltepapier in Metzgereien, Käsereien
1/8	Achtelbogen	250 × 375	Frischhaltepapier in Metzgereien, Käsereien
1/16	Sechzehntelbogen	180 × 250	Frischhaltepapier in Metzgereien, Käsereien
1/32	Zweiunddreißigstelbogen	125 × 180	Zwischenlagen, z. B. bei Wurst, Käse, Konditoreiprodukten
1/64	Vierundsechzigstelbogen	90 × 125	Zwischenlagen, z. B. bei Wurst, Käse, Konditoreiprodukten

Historische Papierformate

historische Papierformate (in mm)

Bezeichnung	Abmessungen
Oktav	142,5 × 225
Quart	225 × 285
Folio	210 × 330
Brief	270 × 420
Kanzlei, Doppelfolio	330 x 420
Propatria	340 x 430
Groß Patria	360 x 430
Bischof	380 × 480
Register, Löwen	400 × 500
Median I	420 × 530
Median	440 × 560
Post	460 × 560
Median II	460 × 590
Klein Royal	480 × 640
Royal	480 × 650
Lexikon	500 × 650
Super Royal	500 × 680
Imperial	570 × 780
Olifant	675 × 1082

Bedeutsam beim Aufstellen von Büchern in einer Bibliothek. "bis/ab Großoktav" (8°), "Folianten".

Notendruck

historische Notendruckformate (in mm)

Formatklasse	Abmessungen
Großpartitur	420 × 680*
	300 × 420
	300 × 400
	285 × 400
	300 × 390
	290 × 350
Quartformat	270 × 340
Bachformat	240 × 325
N4	231 × 303
Oktavformat	170 × 270*
Studienpartitur	170 × 240
Salonorchester	190 × 290
Klavierauszug	190 × 270
Klavierformat	235 × 310
Großmarsch	135 × 190
Marschformat	135 × 170

^* Goldener Schnitt

China

Dieser Artikel oder Abschnitt ist nicht hinreichend mit Belegen (Literatur, Webseiten oder Einzelnachweisen) versehen. Die fraglichen Angaben werden daher möglicherweise demnächst gelöscht. Hilf Wikipedia, indem du die Angaben recherchierst und gute Belege einfügst. Bitte entferne erst danach diese Warnmarkierung. Siehe Diskussion.

Chinesische Papierformate

Name	Format	Größe
		mm × mm
Kai	8	260 × 370
	16	185 × 260
	32	130 × 185
	32 groß	140 × 203

Japan

Die japanische Norm JIS P 0138-61 übernimmt die A- und C-Serien von ISO bzw. DIN, definiert aber eine leicht andere B-Serie: JIS B0 hat eine Fläche von 1,5 m², dem arithmetischen und nicht geometrischen Mittel der Flächen von A0 und 2A0, Breiten und Höhen werden analog zu A ermittelt und entsprechend gerundet.

Gegenüberstellung der DIN-/ISO- und der JIS-B-Reihe (in Millimetern)

	DIN/ISO	JIS
B0	1000 × 1414	1030 × 1456
B1	707 × 1000	728 × 1030
B2	500 × 707	515 × 728
B3	353 × 500	364 × 515
B4	250 × 353	257 × 364
B5	176 × 250	182 × 257
B6	125 × 176	128 × 182
B7	88 × 125	91 × 128
B8	62 × 88	64 × 91
B9	44 × 62	45 × 64
B10	31 × 44	32 × 45

Traditionelle japanische Papierformate
(1 sun = 1000⁄33 mm)

Name	Format	mm × mm	sun × sun
Shiroku-ban	Basis	788 × 1091	26 × 36
	4 × 6/4	264 × 379	8,7 × 12,5
	4 × 6/5	191 × 259
	4 × 6/5	189 × 262
Kiku-ban	Basis	636 × 939	21 × 31
	Kiku 4	227 × 306	7,5 × 10
	Kiku 5	151 × 227	5 × 7,5

USA, Kanada und Lateinamerika

Die ANSI-Reihe baut auf dem „Letter“-Format (ANSI A) auf. Durch Verdoppelung entsteht das jeweils nächstgrößere Format, alternierend in den Seitenverhältnissen 1 : 1,294 (ANSI A, C, E) und 1 : 1,545 (ANSI B, D).

Die in Nordamerika noch üblichen Papierformate folgen keinem einheitlichen Muster und sind ursprünglich zollbasiert (in). Die Reihe A bis E entstammt dem Standard ANSI/ASME Y14.1, andere Größen sind in ANSI X3.151-1987 festgelegt.

Die kanadischen Größen P1-P6 aus dem Standard CAN 2-9.60M sind in Millimetern spezifiert und auf halbe Zentimeter gerundet. Näherungsweise entsprechen sie Zoll-Pendants. Sie lassen sich durch Verdopplung bzw. Halbierung ableiten. Ihre Bedeutung ist auch in Kanada selbst eher gering.

Die nordamerikanische ANSI-Reihe als auch die kanadischen Größen haben jedoch nicht die Vorteile des konstanten 1,414-Verhältnisses der DIN-Reihen (statt dessen abwechselnd ca. 1,30 und 1,55).

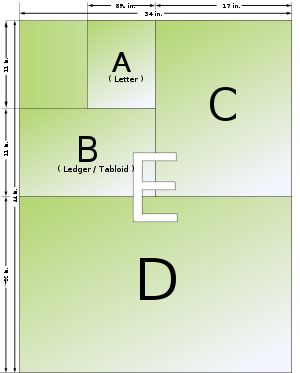
Gebräuchliche nordamerikanische Papierformate

Name	ANSI	in × in	mm × mm	CAN	mm × mm
				P6	107 × 140
Invoice		5½ × 8½	140 × 216	P5	140 × 215
Executive		7¼ × 10½	184 × 267
Legal		8½ × 14	216 × 356
Letter	A	8½ × 11	216 × 279	P4	215 × 280
Ledger, Tabloid	B	11 × 17	279 × 432	P3	280 × 430
Broadsheet	C	17 × 22	432 × 559	P2	430 × 560
	D	22 × 34	559 × 864	P1	560 × 860
	E	34 × 44	864 × 1118

Eine besondere Bedeutung hat hier das Letter-Format mit 8½ × 11 Zoll (216 × 279 mm), da dieses durch den Schriftverkehr auch nach Europa gelangt. Das Blatt ist etwa 6 mm breiter und 18 mm kürzer und mit einer Fläche von 602,7 cm² etwas kleiner als das A4-Blatt mit 625 cm².

Vergleich nordamerikanischer Architektur-/Ingenieurspapierformate

	in × in		mm × mm
Name	Ing.	Arch.	Ing.	Arch.
A	8½ × 11	9 × 12	216 × 279	229 × 305
B	11 × 17	12 × 18	279 × 432	305 × 457
C	17 × 22	18 × 24	432 × 559	457 × 610
D	22 × 34	24 × 36	559 × 864	610 × 914
E	34 × 44	36 × 48	864 × 1118	914 × 1219
F	44 × 68		1118 × 1727

Stellenweise, z. B. im Bibliothekswesen, sind noch heute Formate aus dem 19. Jahrhundert in Gebrauch. Einige Werte haben sich über die Zeit um teilweise mehr als ein Zoll verändert.

Unsystematische historische nordamerikanische Papierformate

Name	in × in	mm × mm
Post	15½ × 19¼	394 × 489
Large Post	16½ × 21	419,1 × 533,4
Elephant	23 × 28	584 × 711
Medium	18 × 23	457,2 × 584,2
Crown	15 × 20	381 × 508
Double Crown	20 × 30	508 × 762
Royal	20 × 25	508 × 635
Quarto	8 × 10	203 × 254
Foolscap	8 × 13	203 × 330
Demy	17½ × 22½	444,5 × 571,5
Double Demy	23½ × 35	597 × 889
Quad Demy	35 × 45	889 × 1143
Dollar Bill	2 9/16 × 6	76 × 178

Zeitplansysteme

Bei Zeitplansystemen (Kalender- und Zeitplan-Ringordner) sind weitere Formate üblich, die je nach Hersteller unterschiedliche Bezeichnungen und Lochungen besitzen. Zum Beispiel

Zeitplansysteme

Name	Firma	Abmessungen
		mm × mm	in × in
WT	tempus.	86 × 145
Monarch	Franklin-Covey	216 × 279	8+1⁄2 × 11
Deskfax	Filofax	176 × 250
Classic	Franklin-Covey	140 × 216	5+1⁄2 × 8+1⁄2
Compact	Franklin-Covey	108 × 171	4+1⁄4 × 6+3⁄4
	Time/System	85 × 169
Pocket	Time/System	100 × 172
	Franklin-Covey	89 × 152	3+1⁄2 × 6
	Filofax	81 × 120
Midi	Chronoplan	96 × 172
Personal, Slimline	Filofax	95 × 171
Mini	Chronoplan	79 × 125
	Filofax	67 × 105
Partner	Time/System	75 × 130
M2	Filofax	64 × 103

Triviales

Europäischen Nutzern begegnet das US-Letter-Format mitunter – wenn auch in eher lästiger Form: amerikanische Computersoftware ist oft als Standardvorgabe auf das Druckformat US-Letter eingestellt und muss angepasst werden. Auch Motorradfahrer kennen das Problem, dass die Kartenfächer von Tankrucksäcken oft nur selbstausgedruckte Karten im US-Letter-Format ungefaltet aufnehmen können.

Scheckkarten, andere Plastik- und Kartonkarten, wie Telefonwertkarten, kleine Z-cards (gefaltet) und viele Visitenkarten messen nach ISO 7810 als Format ID-1 85 mm × 54 mm; real jedoch knapp 86 mm × 54 mm.

Lochkarten mit 187 mm × 83 mm wurden in der elektronischen Datenverarbeitung bis etwa 1985 zur Datenein- und -ausgabe genutzt. Sie dienten mit Aufdruck gelegentlich auch als Rechnung oder Zahlschein (Stromrechnungen E-Werk Wels (A), um 1970).

Als Format für Radtourenbücher mit Spiralbindung zum Umblättern hat sich das Querformat mit 220 mm × 120 mm (+ halbe Spiralbreite) seit 1990 weitgehend durchgesetzt. Es passt in die Deckeltaschen vieler Lenkertaschen, die auch zu Rennlenkern passen, sowie hochkant in (große) Jackeninnentaschen. Gefaltete Wanderkarten weisen ähnlich große Hochformate mit Leporellofaltung auf. Genaue, große Straßenkarten und Stadtpläne sind für weniger windige Umgebung gedacht und daher häufig höher, also 11–12 cm × 25–27 cm. Pläne mit 10 cm × 16 cm und kleiner sind gut brust- und handtaschengängig.

Siehe auch

• Bildformat (Seitenverhältnis) – Papierformate für Kleinbildfotografie
• Buchformat
• Zeitungsformat
• Weltformat

Einzelnachweise

1. ↑ Brief von Georg Christoph Lichtenberg an Johann Beckmann vom 25. Oktober 1786; in: Briefwechsel, Band III (1785–1792), Verlag C. H. Beck, 1990

Literatur

• Deutsches Institut für Normung e.V. (Hrsg.): DIN EN ISO 216:2007-12 : Schreibpapier und bestimmte Gruppen von Drucksachen – Endformate – A- und B-Reihen und Kennzeichnung der Maschinenlaufrichtung (ISO 216:2007); Deutsche Fassung EN ISO 216:2007. Beuth Verlag, Berlin 2007.

Weblinks

• Werner Brefeld: DIN-Papier und der Goldene Schnitt
• Markus Kuhn: International Standard Paper Sizes
• directTOOLS.de: Standard DIN – Papierformate
• IEEE-ISTO 5101.1-2002: The Printer Working Group Standard for Media Standardized Names (PDF)
• Umrechnen Papierformat
• Website über das DIN-A-Format