Pay-As-You-Go

Das Umlageverfahren ist eine Methode zur Finanzierung von Sozialversicherungen, speziell der Altersvorsorge, aber auch von Krankenversicherung und Arbeitslosenversicherung. Die eingezahlten Beiträge werden unmittelbar für die Finanzierung der erbrachten Leistungen herangezogen (d. h. in der Praxis, sie werden sofort wieder an die Leistungsberechtigten ausbezahlt), wobei vom Versicherungsträger in geringem Umfang Rücklagen gebildet werden können (z. B. Nachhaltigkeitsrücklage der gesetzlichen Rentenversicherung). Für seine Beitragsleistung erwirbt der Beitragszahler einen Anspruch auf Leistung im Fall der Bedürftigkeit (Arbeitslosigkeit, Krankheit, Alter). Im Unterschied zum Umlageverfahren werden beim Kapitaldeckungsverfahren die Beiträge angespart und verzinst, um im Leistungsfall (z. B. bei Eintritt in den Ruhestand) ausgezahlt zu werden; oft wird hierbei für jeden Versicherten ein eigenes Konto eröffnet.

Eigenschaften des Umlageverfahrens

Einige grundlegende Eigenschaften des Umlageverfahrens seien kurz am Beispiel der Alterssicherung skizziert.

Anfangsschuld / inhärente Schuld

In einem Umlageverfahren erhält die erste Generation von Empfängern (z. B. Rentnern) Leistungen, ohne dafür (in nennenswertem Umfang) Beitragszahlungen gezahlt zu haben („Einführungsgewinn“). Diesem engl. als „windfall gains“ oder auch „unfunded liability“ (ungedeckte Verbindlichkeit) bezeichnete Geschenk ist für die nachfolgenden Generationen eine inhärente (Anfangs-)Schuld, die sie mit ihren Beiträgen begleichen. Soweit das Umlageverfahren in Kraft bleibt, erhalten sie dafür wiederum Ansprüche gegen ihre Nachfolger. Parallel zum Abbau der Anfangsschuld werden also neue, inhärente Verbindlichkeiten aufgebaut. Dies setzt sich im System fort, das somit stets eine „inhärente Schuld“ aufweist.

Die Höhe der inhärenten Schuld bleibt dabei nicht stabil, sondern ändert sich in dem Maße, wie auf die Beitragszahlungen eine „Rendite“ gewährt wird. Dies sei an einem simplen Beispiel verdeutlicht: Die erste Generation von Rentnern erhalte Gesamttransfers in Höhe von 100 Geldeinheiten, die von den Beschäftigten derselben Periode finanziert werden. Diese Beitragszahler erwarten in der Folgeperiode, idealisierte 25 Jahre später, inflationsbereinigt einen Transfer in Höhe von z. B. 164 Geldeinheiten (entspricht einer jährlichen Rentensteigerung von 2 %). Mathematisch ist die inhärente Schuld damit um den Faktor 1,64 gewachsen (100 * (1 + (n + p)) mit n+p=0,64, siehe Abschnitt „Rendite“), welcher dann ebenfalls von den Beschäftigten finanziert wird, die daraufhin in Periode 3 einen Transfer in Höhe von 269 Geldeinheiten (100 * (1 + (n + p))² erwarten. Generell wird die inhärente Schuld von anfangs 100 nach x Generationen einen Wert von 100 * (1 + (n + p))^{x − 1} erreicht haben. Dementsprechend wird ein Systemwechsel umso teurer, je älter das System wird.

Im Falle einer (inflationsbereinigt) negativen Rendite sinkt umgekehrt die inhärente Schuld. Im hypothetischen Falle einer „letzten“ Generation, die keine Kinder mehr hat, müsste diese Generation die Kosten ihres eigenen und des Ruhestandes der Vorgängergeneration finanzieren.

Auswirkungen von Bevölkerungs- und Einkommensentwicklung

Eine andere Frage ist, wie sich die inhärente Schuld bei den Beitragszahlern niederschlägt. Wächst deren Einkommen synchron zur Rendite des Umlageverfahrens und bleibt auch ihre Zahl in etwa konstant, so verändert sich unabhängig von der absoluten Höhe der inhärenten Schuld für den Einzelnen der prozentuale Anteil seines Einkommens nicht, den er abführen muss, auch wenn der absolute Betrag stetig steigt. Beispiel: 300 Erwerbstätige (E1=300), die im Durchschnitt je 200 Geldeinheiten verdienen (GE1=200), finanzieren mit 100 Geldeinheiten (GR1 = 100) 100 Rentner (R1 = 100). Jeder Erwerbstätige hat dann einen Beitragssatz von 16,6 % (GR1 * R1 / (GE1 * E1). In der nächsten Periode müssen wieder 300 Erwerbstätige (E2) 100 Rentner (R2) finanzieren, allerdings dafür – wegen des o. g. Wachstums – nunmehr 164 Geldeinheiten (GR2=164) aufbringen. Ihre absolute Zahllast ist damit um 64 % gestiegen. Wenn sie aber gleichzeitig selbst Einkommenssteigerungen von 2 % im Jahr erzielt haben, dann ist auch ihr Einkommen auf E2=328 Geldeinheiten angewachsen. Der Beitragssatz, also der prozentuale Anteil ihres Einkommens, den sie abführen müssen, bleibt daher stabil.

Ist die nächste Generation von Einzahlern dagegen kleiner als die erste, etwa weil zu wenig Kinder geboren werden, mehr Menschen arbeitslos oder arbeitsunfähig sind, dann steigt der Beitragssatz – bei E2=200 (d. h. Rückgang der Einzahler um ein Drittel) im Beispiel auf 25 %. Noch stärker fällt die Steigerung aus, wenn der Durchschnittsverdienst langsamer wächst als die Renten, etwa, weil unter den Erwerbstätige der Anteil von Teilzeitarbeitern oder gering qualifizierten Personen ansteigt.

Ausgleich aus Steuermitteln

In der Realität können etwaige Defizite durch Transfers aus dem allgemeinen Steueraufkommen finanziert werden (Schwankungsreserve in Deutschland, auch durch die Ökosteuer). In Deutschland machen Steuertransfers derzeit etwa 1/3 der Ausgaben der gesetzlichen Rentenversicherung aus, das sind ca. 80Mrd € oder ein Drittel des Bundeshaushalts. In dem Maße, in dem diese Steuern wiederum von den Erwerbstätigen finanziert werden, steigt allerdings auch dadurch deren effektive Belastung; in dem Maße, wie sie durch Staatsverschuldung finanziert werden, entsteht eine andere Form der inhärenten Schuld

Rechtfertigung der inhärenten Schuld

Schulden werden meist dadurch gerechtfertigt, dass der Schuldner vom Gläubiger eine Gegenleistung erhalten hat, etwa ein Darlehen oder einen Gegenstand. Im Falle des Umlageverfahrens kann diese Gegenleistung darin gesehen werden, dass die ältere Generation massiv in die Nachfolgegeneration investiert hat: deren Aufzucht und Ausbildung, ohne die ihr Erwerbseinkommen niemals erzielt würde, wurde ja von der Elterngeneration erbracht. So gesehen hat keine Generation, auch nicht die Anfangsgeneration, als solche ein „Geschenk“ erhalten, vielmehr zahlt jeweils die jüngere Generation zurück, was sie zuvor an Zuwendungen erhalten hat.

Eine andere Frage ist, wie innerhalb der Generationen diese Lasten verteilt werden: wer beispielsweise nicht beitragspflichtig ist, der beteiligt sich nicht oder (über Steuertransfers) in ganz anderer Form an den Zahlungen für seine eigenen Eltern/Großeltern. Wer selbst keine Kinder hat, der hat (wieder über Steuern) nur indirekt und in geringerem Umfang Zuwendungen an die Nachfolgegeneration geleistet; wie umfangreich, wie wertvoll und wie effektiv die Zuwendungen des Einzelnen an seine Kinder sind, bleibt bei den heute üblichen Umlagesystemen ebenfalls unberücksichtigt. Mitunter wird versucht, durch besondere Gestaltung auf diese Lastverteilung Einfluss zu nehmen, etwa die Anerkennung von Erziehungsjahren als Beitragszeiten.

Vor allem an solchen Überlegungen entzündet sich die Frage nach der Gerechtigkeit eines Umlageverfahrens und seiner konkreten Ausgestaltung.

genauere Darstellung

Eine mathematische Darstellung der wesentlichen Parameter sieht so aus:

Grundformel

Angenommen, die Beitragszahlungen in einer jeden Periode werden als fixer Prozentsatz vom Lohn der während dieser Periode erwerbstätigen Personen einbehalten. Aus diesen Beitragsleistungen werden die Pensionsleistungen für die während dieser Periode im Ruhestand befindlichen Personen finanziert. In einem reinen Umlagesystem müssen in jeder Periode die gesamten Beitragseinnahmen mit den gesamten Rentenzahlungen übereinstimmen:

Beitragszahlungen in Periode t = Leistungen in Periode t.

Unterstellt man, dass alle Beitragszahler und alle Leistungsempfänger identisch sind, so erhält man formal die folgende Budgetidentität eines Umlageverfahrens:

(1) Z_tw_tτ = E_tb_t

wobei die folgende Notation vereinbart ist:

• Z_t = Zahl der Beitragszahler in Periode t
• E_t = Zahl der Beitragsempfänger in Periode t
• w_t = Lohnsatz in Periode t
• τ = Beitragssatz
• b_t = Einheitsrente in Periode t

Rendite

Die (durchschnittliche) Rendite eines Umlageverfahrens für ein teilnehmendes Individuum errechnet sich aus dem Verhältnis der erhaltenen Leistungen zu den eingezahlten Beiträgen, sinnvoller bereinigt um inflationäre Effekte:

$Rendite = \frac{Barwert\ der\ Leistungen}{Barwert\ der\ Beitraege} - 1$.

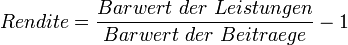Da über die Budgetidentität des Umlageverfahrens die Leistungen den Beiträgen der Folgeperiode entsprechen, entspricht die Rendite des Umlageverfahrens im Durchschnitt der Wachstumsrate der Beiträge.

Die durchschnittliche Rendite auf die Einzahlungen in ein Umlageverfahren lässt sich exemplarisch auch für Gleichung (1) berechnen. Es sei unterstellt, dass ein Individuum in einer Periode t Beitragszahler ist und in der darauf folgenden Periode t+1 Leistungsempfänger (i.a.W., die Länge des Arbeitslebens stimmt überein mit der Länge der Pensionszeit). Ein Individuum zahlt somit den Betrag w_tτ ein und bekommt eine Rente in der Höhe b_{t + 1}. Die resultierende Rendite ist:

(2) $\frac{b_{t+1} - w_t \tau}{w_t \tau}=\frac{(Z_{t+1}w_{t+1}\tau)/E_{t+1}}{w_t\tau}-1=(1+n)(1+p)-1\approx n+p$

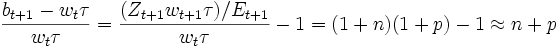
wobei folgende Notation verwendet wird:

• n = Wachstumsrate der Bevölkerung
• p = Wachstumsrate des Lohnsatzes

Dabei gilt: E_{t + 1} = Z_t, w_{t + 1} = w_t(1 + p), E_{t + 1} = E_t(1 − n) und $b_{t+1}=\frac{Z_{t+1}w_{t+1}\tau}{E_{t+1}}$

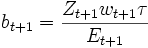
Da das Produkt np numerisch vernachlässigt werden kann, lässt sich die Rendite approximieren durch n + p. In einem „gereiften“ Umlagesystem ist damit die Beitragsrendite gleich der Summe aus Lohn- und Bevölkerungswachstum. Dieses Ergebnis wurde zuerst von Aaron (1966) gezeigt. Damit sinkt die Rendite umlagefinanzierter Systeme, wenn das Bevölkerungswachstum sinkt oder gar negativ wird bzw. die Lohnsatzsteigerungen gering ausfallen.

Demographische Veränderungen

Die Auswirkung demographischer Veränderungen auf das Umlageverfahren kann durch eine Umstellung von Gleichung (1) verdeutlicht werden:

$\tau=\frac{E_t}{Z_t}\frac{b_t}{w_t}$.

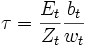Diese Formulierung bestimmt den budgetausgleichenden Beitragssatz, wenn eine gewünschte Rentenhöhe vorgegeben ist. Der Ausdruck

$\frac{E_t}{Z_t}$

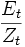
entspricht der Anzahl von Leistungsempfängern je Beitragszahler (auch Altersabhängigkeitsquotient, Alterslastquotient oder old age dependency ratio genannt), der Ausdruck

$\frac{b_t}{w_t}$

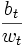
dem Verhältnis von (Durchschnitts-)Rentenbetrag zu (Durchschnitts-)Lohnsatz (die Lohnersatzquote).

Wenn nun das System finanziellen Druck erfährt, bieten sich grundsätzlich die folgenden Optionen an, die Budgetidentität wiederherzustellen:

• Erhöhung des Beitragssatzes τ
• Senkung der Lohnersatzquote (im wesentlichen nur durch Senkung der Durchschnittsrente möglich)
• Senkung des Alterslastquotienten (im wesentlichen nur durch eine Erhöhung der Lebensarbeitszeit möglich, d. h. späterer Renteneintritt)

Umlageverfahren in der Praxis

Situation in Deutschland

In Deutschland wird das Umlageverfahren bei den Sozialversicherungen (Rente, gesetzlicher Kranken-, Arbeitslosen- und Unfall- sowie der Pflegeversicherung) angewendet. Die Höhe der Beiträge richtet sich global nach den Kosten für die erbrachten Leistungen, wobei jedoch einkommensorientierte Bemessungsrichtlinien sicherstellen sollen, dass die individuelle Beitragsbelastung ein bestimmtes Maß nicht übersteigt. Auf der anderen Seite gibt es auch Beitragsuntergrenzen (im Jahr 2005 z. B. ca. 260 EUR monatlich als Mindestbeitrag für die gesetzliche Krankenversicherung).

Rentenversicherung durch den Generationenvertrag

In Deutschland wurde das Umlageverfahren 1957 in der Rentenreform 1957 für die Vollrente in Höhe von 70 % des letzten Bruttolohns durchgesetzt. Vorher gab es eine kapitalgedeckte Sparrente. Die theoretische Grundlage für die Einführung des Umlageverfahrens (§ 153 SGB VI) lieferte der Nationalökonom und Vertreter der katholischen Soziallehre Wilfrid Schreiber (1904–1975) mit seiner Arbeit „Existenzsicherheit in der industriellen Gesellschaft“. Er sprach dort von einem „Solidar-vertrag zwischen jeweils zwei Generationen“. Allerdings wurde Schreibers Konzept des Generationenvertrags von Adenauer nicht vollständig umgesetzt. Dieses hatte eine breitere finanzielle Basis durch Einbeziehung von Freiberuflern und Selbständigen sowie die Einrichtung einer „Kinder- und Jugendrente“ vorgesehen.

Umlageverfahren in anderen Ländern

• USA, angewandt bei der staatlichen Rentenversicherung Social Security
• Schweiz, angewandt in der ersten Säule des Drei Säulen-Systems
• Japan
• Österreich

Probleme in der Finanzierung der Umlageverfahren

Aufgrund steigender Kosten im Gesundheitswesen, zunehmender Lebenserwartung und damit auch wachsender Pflegekosten bei gleichzeitig einbrechenden Einnahmen wegen demographischer Verschiebungen (sinkende Geburtenrate, Überalterung der Gesellschaft), sinkender Lohnquote, Massenarbeitslosigkeit sowie versicherungsfremder Entnahmen und wirtschaftlicher Krisen in vielen Industrienationen wird die Finanzierung der Sozialversicherungen durch Umlageverfahren zunehmend in Frage gestellt. In Deutschland wurde während der ersten Legislaturperiode der Regierung Schröder versucht, eine kapitalgedeckte zweite Säule der Rentenversicherung zu errichten. Zur Zeit (2005) erhalten die Rentenversicherungen in Deutschland aufgrund nicht ausreichender Mittel des Umlagesystems einen Zuschuss in Höhe von etwa 80 Milliarden Euro jährlich aus Steuermitteln.

Siehe auch

• Mackenroth-These
• Regelaltersrente
• Renteneintrittsalter

Literatur und Links

• Aaron, H. (1966). The social insurance paradox. Canadian Journal of Economics and Political Science 32(3), 371–374.
• Social Security Administration (USA). Social Security Programs around the world