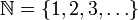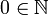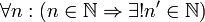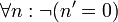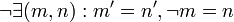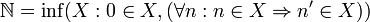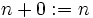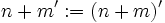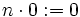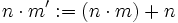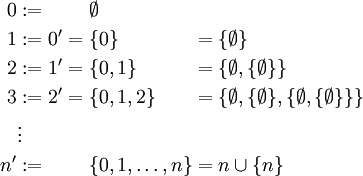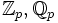- Peano-Axiom
-
ℕ
Die natürlichen Zahlen sind die beim Zählen verwendeten Zahlen 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 usw. Oft wird auch die 0 (Null) zu den natürlichen Zahlen gerechnet. Sie bilden bezüglich der Addition und der Multiplikation einen (additiv und multiplikativ) kommutativen Halbring.
Inhaltsverzeichnis
Bezeichnungen und Konventionen für die Menge der natürlichen Zahlen
Die Menge der natürlichen Zahlen, Formelzeichen
enthält je nach Definition die positiven ganzen Zahlen, also
oder die nichtnegativen ganzen Zahlen
(Diese Schreibweisen werden in der Literatur uneinheitlich verwendet)
Für jede der beiden unterschiedlichen Konventionen gibt es sowohl historische als auch praktische Gründe. Die Definition ohne die Null steht in der älteren Tradition, da die natürlichen Zahlen ohne die Null lange Zeit die einzigen bekannten Zahlen waren: In Europa wurde erst ab dem 13. Jahrhundert mit der Null gerechnet. In manchen Gebieten der Mathematik wie der Zahlentheorie, in denen die multiplikative Struktur der natürlichen Zahlen im Vordergrund steht, ist aufgrund der Sonderrolle der Null bei der Multiplikation die Definition ohne Null häufiger anzutreffen. Aber beispielsweise in der mathematischen Logik, der Mengenlehre oder in der Informatik (siehe z.B. Dijkstra[1]) vereinfacht die Definition mit Null die Darstellung. In der DIN-Norm 5473 wird die Null zu den natürlichen Zahlen gezählt. Im Zweifelsfall bietet es sich an, die verwendete Definition explizit anzugeben.
Als Symbol für die Menge der natürlichen Zahlen führte Peano 1889 das
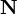 ein.[2] Weil dies handschriftlich nur schwer darstellbar ist, variierte man es im Tafelbild zu dem Strichbuchstaben
ein.[2] Weil dies handschriftlich nur schwer darstellbar ist, variierte man es im Tafelbild zu dem Strichbuchstaben 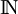 , welcher sich zusammen mit der Variante
, welcher sich zusammen mit der Variante 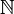 im Laufe der Zeit auch im Drucksatz weitgehend durchsetzte, sodass heute fast nur noch die Symbole
im Laufe der Zeit auch im Drucksatz weitgehend durchsetzte, sodass heute fast nur noch die Symbole 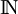 und
und 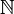 für die natürlichen Zahlen verwendet werden. Die gleiche Entwicklung fand auch bei den anderen Doppelstrich-Symbolen wie beispielsweise
für die natürlichen Zahlen verwendet werden. Die gleiche Entwicklung fand auch bei den anderen Doppelstrich-Symbolen wie beispielsweise  und
und  statt.
statt.Da nicht überall die 0 als ein Element der natürlichen Zahlen angesehen wird, ist es sinnvoll, von positiven (1, 2, 3, …) und nicht-negativen (0, 1, 2, …) ganzen Zahlen zu sprechen.
In Texten, in denen das Symbol
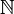 für die Menge der natürlichen Zahlen ohne Null verwendet wird, wird zur Unterscheidung das Symbol
für die Menge der natürlichen Zahlen ohne Null verwendet wird, wird zur Unterscheidung das Symbol 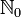 oder
oder 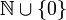 für die Menge der natürlichen Zahlen einschließlich der Null benutzt.
für die Menge der natürlichen Zahlen einschließlich der Null benutzt.
Falls jedoch das Symbol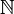 für die Menge der natürlichen Zahlen mit Null verwendet wird, wird meist
für die Menge der natürlichen Zahlen mit Null verwendet wird, wird meist  ,
, 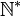 ,
, 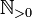 ,
, 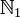 oder
oder 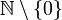 für die Menge der natürlichen Zahlen ohne 0 geschrieben. Nach DIN 5473 sollte
für die Menge der natürlichen Zahlen ohne 0 geschrieben. Nach DIN 5473 sollte 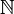 für die nicht-negativen und
für die nicht-negativen und 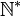 für die positiven natürlichen Zahlen verwendet werden.
für die positiven natürlichen Zahlen verwendet werden.Peano-Axiome
Für eine formale Definition der Menge der natürlichen Zahlen und der zugehörigen Rechenregeln ist es letztlich nicht relevant, ob man auch die Null als natürliche Zahl bezeichnet oder nicht. Im folgenden wird jedoch zugunsten der Verständlichkeit davon ausgegangen, dass 0 eine natürliche Zahl ist. Peano selbst begann die natürlichen Zahlen in seinen Axiomen mit der 1 statt mit der 0 [3]; aber die behandelten Axiome und Rechenregeln lassen sich analog in beiden Fällen anwenden.
Wichtig ist, dass es ein Startelement gibt und zu jedem Element einen Nachfolger, denn die natürlichen Zahlen hängen eng mit dem Prinzip der mathematischen Induktion zusammen.
Es folgt eine Definition der Menge der natürlichen Zahlen
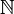 durch Axiome, die erstmals 1889 von Giuseppe Peano angegeben wurden. Diese Axiome werden Peano-Axiome genannt, obwohl sie eigentlich genauer Peano-Dedekindsche Axiome genannt werden müssten, da Peano lediglich die von Richard Dedekind in dessen Schrift Was sind und was sollen die Zahlen? (1888) dargestellten Axiome in eine logische Formelsprache übersetzt hat.
durch Axiome, die erstmals 1889 von Giuseppe Peano angegeben wurden. Diese Axiome werden Peano-Axiome genannt, obwohl sie eigentlich genauer Peano-Dedekindsche Axiome genannt werden müssten, da Peano lediglich die von Richard Dedekind in dessen Schrift Was sind und was sollen die Zahlen? (1888) dargestellten Axiome in eine logische Formelsprache übersetzt hat.- 0 ist eine natürliche Zahl.
- Zu jeder natürlichen Zahl n gibt es genau einen Nachfolger n', der ebenfalls eine natürliche Zahl ist.
- Es gibt keine natürliche Zahl, deren Nachfolger 0 ist.
- Jede natürliche Zahl ist Nachfolger höchstens einer natürlichen Zahl.
- Von allen Mengen X, welche
-
- die Zahl 0 und
- mit jeder natürlichen Zahl n auch stets deren Nachfolger n'
- enthalten, ist die Menge der natürlichen Zahlen die kleinste.
-
Die Axiome verwenden dabei die Begriffe 0, Zahl und Nachfolger. Bertrand Russell wies darauf hin, dass man damit nicht nur die natürlichen Zahlen, sondern jedes beliebige (abzählbare) Zahlensystem definieren kann. Man definiere z. B. 7/16 als 0 und erzeuge einen Nachfolger durch Addition von 1/16.
Das letzte Axiom nennt man auch das Induktionsaxiom, es bildet die Grundlage für die Beweismethode der vollständigen Induktion. Es gibt verschiedene Möglichkeiten, die Peano-Axiome zu formalisieren. Eine (wenn auch nicht die beste, da hier der Mengenbegriff vorausgesetzt wird) ist die folgende:
Hiervon ausgehend werden auf
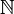 die Addition und Multiplikation definiert. Man setzt
die Addition und Multiplikation definiert. Man setztund dann
Das Induktionsaxiom garantiert jeweils, dass Addition und Multiplikation wohldefiniert sind.
Setzt man nun noch 1 = 0', ergibt sich n' = n + 1.
Die Peano-Axiome bilden ein Axiomensystem der Prädikatenlogik zweiter Stufe, da neben Variablen für Zahlen im Induktionsaxiom auch die Mengenvariable X vorkommt. Ersetzt man dieses Axiom durch die entsprechenden unendlich vielen Axiome erster Stufe, so gelangt man zur Peano-Arithmetik.
Von Neumanns Modell der natürlichen Zahlen
Peano beschrieb mit seinem Axiom-System zwar die Eigenschaften von natürlichen Zahlen, sah aber keine Notwendigkeit, deren Existenz zu beweisen. John von Neumann gab eine Möglichkeit an, die natürlichen Zahlen durch Mengen darzustellen, d.h. er beschrieb ein mengentheoretisches Modell der natürlichen Zahlen.
Zur Erklärung: Für das Startelement, die „0“, ist die leere Menge
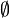 gewählt worden. Die „1“ ist hingegen die Menge, welche die leere Menge als Element enthält. Dies sind verschiedene Mengen, denn die „0“ enthält kein Element, wohingegen die „1“ genau ein Element enthält. Jeder Nachfolger ist vom Vorgänger verschieden, da die Nachfolgermenge ein Element mehr enthält, als die Vorgängermenge, nämlich den Vorgänger selbst.
gewählt worden. Die „1“ ist hingegen die Menge, welche die leere Menge als Element enthält. Dies sind verschiedene Mengen, denn die „0“ enthält kein Element, wohingegen die „1“ genau ein Element enthält. Jeder Nachfolger ist vom Vorgänger verschieden, da die Nachfolgermenge ein Element mehr enthält, als die Vorgängermenge, nämlich den Vorgänger selbst.Die Existenz jeder einzelnen natürlichen Zahl ist mengentheoretisch schon durch recht schwache Forderungen gesichert. Für die Existenz der Menge aller natürlichen Zahlen benötigt man jedoch in der Zermelo-Fraenkel-Mengenlehre ein eigenes Axiom, das so genannte Unendlichkeitsaxiom.
Eine Verallgemeinerung dieser Konstruktion ergibt die Ordinalzahlen.
Die natürlichen Zahlen als Teilmenge der reellen Zahlen
Die Einführung der natürlichen Zahlen mit Hilfe der Peano-Axiome ist eine Möglichkeit, die Theorie der natürlichen Zahlen zu begründen. Als Alternative kann man beim Körper der reellen Zahlen
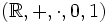 axiomatisch einsteigen und die natürlichen Zahlen als Teilmenge von
axiomatisch einsteigen und die natürlichen Zahlen als Teilmenge von  definieren. Dazu benötigt man zunächst den Begriff einer induktiven Menge.
definieren. Dazu benötigt man zunächst den Begriff einer induktiven Menge.Eine Teilmenge M von
 heißt induktiv, wenn folgende Bedingungen erfüllt sind:
heißt induktiv, wenn folgende Bedingungen erfüllt sind:- 0 ist Element von M
- Ist x Element von M, so ist auch x + 1 Element von M
Dann ist
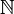 der Durchschnitt aller induktiven Teilmengen von
der Durchschnitt aller induktiven Teilmengen von  .
.Einführung der natürlichen Zahlen nach Russell (historisch)
Der im Folgenden vorgestellte Ansatz von Bertrand Russell ist aus heutiger Sicht als Definition der natürlichen Zahlen aufgrund von mengentheoretischen Schwierigkeiten unbrauchbar. Beispielsweise ist die unten definierte natürliche Zahl 1 keine Menge, sondern eine echte Klasse; infolgedessen ist es unmöglich, über die Gesamtheit der so definierten natürlichen Zahlen zu sprechen, da echte Klassen selbst weder Elemente von Mengen noch von Klassen sein können.
Die natürlichen Zahlen können jeweils als Gesamtheit der Objekte der jeweiligen Kardinalität definiert werden. So definiert Russell zunächst:
- Eine Menge wird einer anderen Menge äquivalent genannt, wenn es eine ein-eindeutige Beziehung gibt, deren Bereich aus der einen Menge besteht, während die andere Menge den inversen Bereich bildet.
Es gelten für diesen Äquivalenzbegriff die Äquivalenzeigenschaften, so dass die auf diese Weise entstehenden Äquivalenzklassen als Repräsentanten für die natürlichen Zahlen dienen können:
- Die Zahl einer Menge ist die Menge aller ihr äquivalenten Mengen.
Mit diesem Zahlbegriff sind sogar beliebige Kardinalitäten von Mengen beschrieben. (Heute nennt man diese Zahlen Kardinalzahlen.) Für die natürlichen Zahlen müssen wir uns auf die endlichen Mengen beschränken. Die endlichen Mengen fasst Russell schrittweise zusammen:
- Die Zahl 0 ist die Menge, deren einziges Element die leere Menge ist. (Man bedenke: zwei Mengen sind gleich, wenn jedes Element der einen Menge in der anderen vorkommt und umgekehrt. Daher gibt es nur eine einzige leere Menge.)
Russell definiert jetzt Nachfolger und Vorgänger von Zahlen:
- Sei A eine Menge und x ein Element, das in A nicht vorkommt. Der Nachfolger der Zahl der Elemente von A ist die Zahl der Elemente von
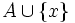 .
. - Sei A eine nichtleere Menge und x ein Element von A, dann heißt die Zahl der Elemente von
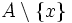 der Vorgänger von der Zahl von A.
der Vorgänger von der Zahl von A.
Damit hat Russell jetzt das notwendige Handwerkszeug zusammen und kann definieren, was die endlichen Zahlen sind:
- a) 0 ist endlich.
- b) Eine Zahl ungleich 0 ist endlich, wenn sie einen Vorgänger hat, der endlich ist.
(Diese Definition endlicher Mengen ist aus heutiger Sicht nicht haltbar, da ihre Präzisierung entweder den Begriff der natürlichen Zahl verwenden oder eine mengentheoretisch unzulässige Konstruktion verwenden muss. Dies ließe sich jedoch durch Verwendung des Begriffes der Dedekind-Endlichkeit umgehen.)
Schließlich legt Russell fest:
- Eine natürliche Zahl ist etwas, was Zahl einer endlichen Menge ist.
Die Erläuterungen Russells gehen im Wesentlichen auf Gottlob Freges „Grundlagen der Arithmetik“ (1884) zurück; anstatt von „Mengen“ zu sprechen, bezieht sich Frege darin auf „Begriffsumfänge“.
Primzahlen
Die Primzahlen stellen die multiplikativen Grundbausteine der natürlichen Zahlen dar.
Es gilt der Fundamentalsatz der Arithmetik:
Jede natürliche Zahl außer der Null besitzt eine eindeutige Primfaktorzerlegung, d. h. sie lässt sich, von der Reihenfolge der Faktoren abgesehen, auf genau eine Art als Produkt von Primzahlen darstellen.
Produkte mit nur einem oder gar keinem Faktor sind dabei zugelassen. Nach dieser Definition hat das sogenannte leere Produkt aus null Faktoren den Wert 1 und stellt damit die Primfaktorzerlegung der 1 dar.
Die alternative Definition in der Zahlentheorie Fundamentalsatz der elementaren Zahlentheorie (Quelle: H. Scheid: Zahlentheorie) lautet:
Jede natürliche Zahl n > 1 lässt sich als Produkt von Primzahlen darstellen. Abgesehen von der Reihenfolge der Faktoren ist diese Darstellung eindeutig, n besitzt also ‚genau eine‘ Primfaktorzerlegung.
Die Zahl 1 hat keine Primfaktorzerlegung, da sie nur einen Teiler (sich selbst) hat und somit keine Primteiler existieren.
Siehe auch
Quellen
- ↑ EWD831: Why numbering should start at zero
- ↑ Peano: Arithmetices principia nova methodo exposita, Turin 1889
- ↑ mathematik.ch
Literatur
- Bertrand Russell: Einführung in die mathematische Philosophie. Drei-Masken, München 1919, F. Meiner, Hamburg 2006. ISBN 3-7873-1602-7
- Johannes Lenhard, Michael Otte (Hrsg.): Einführung in die mathematische Philosophie. F. Meiner, Hamburg 2002. ISBN 3-7873-1602-7
- Harald Scheid: Zahlentheorie. BI-Wiss.-Verl., Mannheim 1994 (2.Aufl.). ISBN 3-411-14842-X
Natürliche Zahlen
 | Ganze Zahlen
| Ganze Zahlen  | Rationale Zahlen
| Rationale Zahlen  | Reelle Zahlen
| Reelle Zahlen  | Komplexe Zahlen
| Komplexe Zahlen  | Quaternionen
| Quaternionen  | Oktaven
| Oktaven 
Wikimedia Foundation.