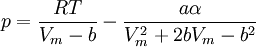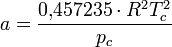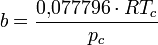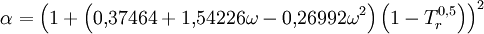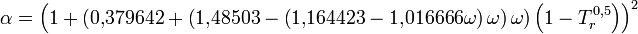Zustandsgleichung von Peng-Robinson — Die Zustandsgleichung von Peng Robinson[1] ist eine Zustandsgleichung für reale Gase. Sie lautet: Die einzelnen Formelzeichen stehen für folgende Größen: Vm … Deutsch Wikipedia
Energiegleichung — Als Zustandsgleichung wird der funktionale Zusammenhang zwischen thermodynamischen Zustandsgrößen bezeichnet, mit deren Hilfe sich der Zustand eines thermodynamischen Systems beschreiben lässt. Dabei wählt man eine der Zustandsgrößen als… … Deutsch Wikipedia
Kalorische Zustandsgleichung — Als Zustandsgleichung wird der funktionale Zusammenhang zwischen thermodynamischen Zustandsgrößen bezeichnet, mit deren Hilfe sich der Zustand eines thermodynamischen Systems beschreiben lässt. Dabei wählt man eine der Zustandsgrößen als… … Deutsch Wikipedia
Thermische Zustandsgleichung — Als Zustandsgleichung wird der funktionale Zusammenhang zwischen thermodynamischen Zustandsgrößen bezeichnet, mit deren Hilfe sich der Zustand eines thermodynamischen Systems beschreiben lässt. Dabei wählt man eine der Zustandsgrößen als… … Deutsch Wikipedia
Zustandsfunktion — Als Zustandsgleichung wird der funktionale Zusammenhang zwischen thermodynamischen Zustandsgrößen bezeichnet, mit deren Hilfe sich der Zustand eines thermodynamischen Systems beschreiben lässt. Dabei wählt man eine der Zustandsgrößen als… … Deutsch Wikipedia
Zustandsvariable — Als Zustandsgleichung wird der funktionale Zusammenhang zwischen thermodynamischen Zustandsgrößen bezeichnet, mit deren Hilfe sich der Zustand eines thermodynamischen Systems beschreiben lässt. Dabei wählt man eine der Zustandsgrößen als… … Deutsch Wikipedia
Zustandsgleichung — Als Zustandsgleichung wird der funktionale Zusammenhang zwischen thermodynamischen Zustandsgrößen bezeichnet, mit deren Hilfe sich der Zustand eines thermodynamischen Systems beschreiben lässt. Dabei wählt man eine der Zustandsgrößen als… … Deutsch Wikipedia
Reales Gas — Das reale Gas ist ein Begriff aus der Thermodynamik. Es steht im Zusammenhang mit dem Begriff des idealen Gases und ist dessen „realistischeres“ Gegenstück. Während das ideale Gas aus Teilchen besteht, die untereinander ausschließlich über… … Deutsch Wikipedia
Gasgesetze — Als Gasgesetze bezeichnet man physikalische Gesetze, die unter anderem zwischen den Zustandsgrößen Druck p, Volumen V, Temperatur T und Stoffmenge n beziehungsweise Masse m oder Teilchenzahl N eine Beziehung herstellen und über diese die… … Deutsch Wikipedia
PSRK — (kurz für Predictive Soave Redlich Kwong) [1] ist ein Abschätzverfahren für die Berechnung von Phasengleichgewichten von Gemischen chemischer Stoffe. Die ursprüngliche Zielsetzung war es, die Eigenschaften von Gemischen, die auch überkritische… … Deutsch Wikipedia