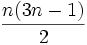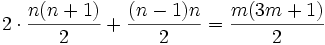- Pentagonalzahl
-
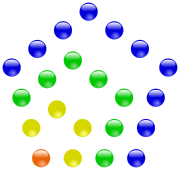
Eine Fünfeckszahl oder Pentagonalzahl ist eine Zahl, die das Konzept der Dreiecks- und Quadratzahlen auf das regelmäßige Fünfeck erweitert. Allerdings ist das dabei entstehende Muster weit weniger symmetrisch als das der Dreiecks- und Quadratzahlen. Die n-te Fünfeckszahl entspricht der Anzahl der Kugeln, die man zum Legen eines Musters mit n regelmäßigen Fünfecken benötigt, die eine gemeinsame Ecke haben. Die ersten Fünfeckszahlen sind
Bei einigen Autoren ist die Null keine Fünfeckszahl, sodass die Zahlenfolge erst mit der Eins beginnt.
Die n-te Fünfeckszahl lässt sich mit der Formel
berechnen.
Die wichtigste Aussage über Fünfeckszahlen ist der Pentagonalzahlensatz.
Fünfeckszahlen der zweiten Art
Setzt man für n eine negative ganze Zahl ein, so bekommt man Fünfeckszahlen zweiter Art oder auch Kartenhauszahlen. Kartenhauszahlen deswegen, weil die Zahlen angeben, wieviele Karten benötigt werden, um ein Kartenhaus mit n Etagen zu bauen.
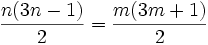 für
für 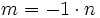 und
und 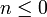
Die Folge der Kartenhauszahlen beginnt:
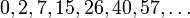 (Folge A005449 in OEIS)
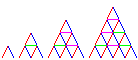
(Folge A005449 in OEIS)Die Kartenhauszahlen lassen sich als Summe von Dreieckszahlen erzeugen:
Kartenhauszahlen als Summe von Dreieckszahlen Weblinks
Wikimedia Foundation.