Perrinsche Pseudoprimzahlen

Die Perrin-Folge ist eine algebraische Zahlenfolge. Sie ist ähnlich der Fibonacci-Folge eine rekursive Folge, bei der ein Glied dieser Folge die Summe von Vorgängergliedern ist.

Geschichte

1876 hat Édouard Lucas an einer Folge mit der Bildungsregel P(n) = P(n − 2) + P(n − 3) gearbeitet, die jedoch andere Startwerte besaß, als die Perrin-Folge. 1899 hat R. Perrin Lucas′ Ideen weiterentwickelt, und aus Lucas Bildungsregel mit den Startwerten: P(0) = 3, P(1) = 0 und P(2) = 2 eine Folge aufgestellt, die als Perrin-Folge bekannt geworden ist.

Definition

Die Glieder der Perrin-Folge werden wie folgt definiert:

P_n = P_{n − 2} + P_{n − 3}

P₀ = 3

P₁ = 0

P₂ = 2

Daraus ergibt sich folgende Folge:

3 0 2 3 2 5 5 7 10 12 17 22 29 39 51 68 90 119 158 ... (Folge A001608 in OEIS)

Eigenschaften

Bestimmte n haben nun die Eigenschaft, P(n) zu teilen:

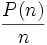
$\frac{P(n)}{n}$	0	1	1	1	1	2	3	7	11	28	120	197
P(n)	0	2	3	5	7	22	39	119	209	644	3480	6107
n	1	2	3	5	7	11	13	17	19	23	29	31

Interessanterweise sind alle n (in der Tabelle) die P(n) teilen, Primzahlen, mit Ausnahme von n=1. Tatsächlich hat man bewiesen, das wenn n eine Primzahl ist, n P(n) teilen muss. Lässt sich der Schluss daraus ziehen, dass, wenn n P(n) teilt, n eine Primzahl sein muss? Nein, es gibt auch zusammengesetzte n, die P(n) teilen. Diese zusammengesetzten n nennt man Perrinsche Pseudoprimzahlen

perrinsche Pseudoprimzahlen
271441	521 * 521
904631	7 * 13 * 9941
16532714	2 * 11 * 11 * 53 * 1289
24658561	19 * 271 * 4789
27422714	2 * 11 * 11 * 47 * 2411
27664033	3037 * 9109
46672291	4831 * 9661
102690901	5851 * 17551
130944133	6607 * 19819
196075949	5717 * 34297
214038533	8447 * 25339
517697641	6311 * 82031
545670533	13487 * 40459
801123451	8951 * 89501
855073301	16883 * 50647
903136901	17351 * 52051
970355431	22027 * 44053

Weblinks

• Perrin Pseudoprimes