Pfeilparadoxon

Im Pfeil-Paradoxon denkt Zenon von Elea über die Wirklichkeit von Bewegung nach.

Zenon sagt, dass ein fliegender Pfeil in jedem Moment seiner Flugbahn einen bestimmten, exakt umrissenen Ort einnimmt. An einem exakt umrissenen Ort befindet sich der Pfeil in Ruhe, denn an einem Ort kann er sich nicht bewegen. Da sich der Pfeil in jedem Moment also in Ruhe befindet, müsste er sich insgesamt in Ruhe befinden. Paradox: Wir nehmen aber an, dass der Pfeil fliegt.

Die Ausführung von Zenon, dass der Pfeil an einem Ort in Ruhe sei und sich nicht bewege, ist ein deutlicher Hinweis darauf, dass das Konzept des infinitesimal Kleinen oder – anders gesagt – der Grenzwertbegriff in der damaligen Zeit nicht geläufig war. Ausformuliert wurde dieses Konzept erst zwei Jahrtausende später von Isaac Newton und Gottfried Wilhelm Leibniz (unabhängig voneinander). Zu jedem Zeitpunkt t befindet sich der Pfeil genau an einem Ort 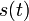$s(t)\!\,$, und zum nächsten Zeitpunkt t'>t bereits an einem anderen Ort s(t'). Die Geschwindigkeit 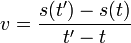$v = \frac{s(t') - s(t)} {t' - t}$ bleibt in einem Inertialsystem (also ohne Beschleunigungen oder Abbremsungen) dabei für alle t' gleich, also auch im Grenzfall 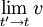$\lim_{t' \to t} v$. Wenn Zenon also von einem Pfeilort 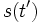$s(t')\!\,$ zu einem Zeitpunkt 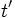$t'\!\,$ redet, haben wir auch in diesem Fall die konstante Geschwindigkeit v vorliegen.

Das Paradoxon wie auch das bekanntere Paradoxon von Achilles und der Schildkröte haben auch bei der Benennung des Quanten-Zeno-Effekts ihre Rolle gespielt.

Siehe auch

• Zenonische Paradoxien

Literatur

• Frank Arntzenius: Are There Really Instantaneous Velocities?’, in: The Monist 83 (2000), 187-208.
• Ofra Magidor: Another note on Zeno’s arrow, in: Phronesis 53 (2008), 359-272 (Draft, für Abonnenten) (dort weitere Literatur)

Weblinks

• Eintrag in der Stanford Encyclopedia of Philosophy (englisch, inklusive Literaturangaben)Vorlage:SEP/Wartung/Parameter 1 und weder Parameter 2 noch Parameter 3