- Phongmodell
-
Das Phong-Beleuchtungsmodell ist ein Beleuchtungsmodell in der 3D-Computergrafik, das dazu verwendet wird, die Beleuchtung von Objekten zu berechnen. Das Modell wurde nach seinem Entwickler Bui-Tuong Phong benannt und erstmals 1975 vorgestellt (Bui-Tuong Phong : Illumination for Computer Generated Pictures, Juni 1975).
Das Phong-Modell ist zur Darstellung von glatten, plastikähnlichen Oberflächen geeignet. Dabei wird das Glanzlicht der Oberfläche durch den Term cosn(θ) beschrieben, wobei der Parameter n die „Rauhigkeit“ der Oberfläche bestimmt.
Es handelt sich um ein vollständig empirisches Modell, das auf keinerlei physikalischer Grundlage aufbaut. So erfüllt es zum Beispiel den Energieerhaltungssatz nicht, der vorschreibt, dass eine Oberfläche nicht mehr Licht, als von der Lichtquelle zur Verfügung gestellt wird, reflektieren kann. Zudem ist es relativ langsam zu berechnen. Das alternative Schlick-Beleuchtungsmodell vermeidet beide Nachteile.
Trotz seiner Mängel ist es noch häufig wesentlicher Bestandteil vieler gängiger 3D-Darstellungsverfahren.
Inhaltsverzeichnis
Formel
Abstraktionen des Phong-Beleuchtungsmodelles
- Lichtquellen sind punktförmig
- die Geometrie der Oberflächen, außer den Oberflächennormalen, wird ignoriert
- diffuse und spiegelnde Reflexion wird nur lokal modelliert
- ambiente Reflexion wird global modelliert
Zusammensetzung des reflektierten Lichtes
Im Phong-Beleuchtungsmodell wird die Reflexion von Licht als Kombination aus ambienter, ideal diffuser und ideal spiegelnder Reflexion beschrieben.
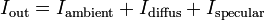
Die Beschreibung der einzelnen Komponenten wird nachfolgend gezeigt.
Ambiente Komponente des reflektierten Lichtes
Die ambiente Komponente des reflektierten Lichts ist unabhängig vom Einfallswinkel des Lichtstrahls der Punktlichtquelle und vom Blickwinkel des Beobachters der Szene. Sie ist abhängig von dem für alle Punkte auf allen Oberflächen konstanten Umgebungslicht, und einem empirisch bestimmten Reflexionsfaktor (Materialkonstante).
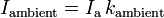
mit
- Ia ... Intensität des Umgebungslichts
- kambient ... Materialkonstante
Diffuse Komponente des reflektierten Lichtes
Bei diffuser Reflexion wird das Licht unabhängig vom Standpunkt des Betrachters in alle Richtungen reflektiert (Lambertsches Gesetz). Die Lichtstärke des reflektierten Lichts der Punktlichtquelle hängt dennoch vom Einfallswinkel ab, da sich die Beleuchtungsstärke der Oberfläche mit dem Einfallswinkel ändert. Somit ist die Lichtstärke der diffusen Komponente vom Einfallswinkel des Lichtstrahls der Punktlichtquelle und von einem empirisch bestimmten Reflexionsfaktor (Materialkonstante) abhängig, jedoch vom Blickwinkel des Beobachters der Szene unabhängig.
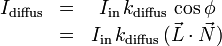
mit
- Iin ... Lichtstärke des einfallenden Lichtstrahls der Punktlichtquelle
- kdiffus ... empirisch bestimmter Reflexionsfaktor für diffuse Komponente der Reflexion
- φ ... Winkel zwischen Normalenvektor der Oberfläche
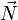 und Einheitsvektor in Richtung des einfallenden Lichtstrahls
und Einheitsvektor in Richtung des einfallenden Lichtstrahls 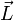
Spiegelnde Komponente des reflektierten Lichtes
Bei spiegelnder Reflexion wird das Licht in einer gewissen Umgebung der idealen Reflexionsrichtung reflektiert. Die Lichtstärke des reflektierten Lichtes ist vom Einfallswinkel des Lichtstrahls der Punktlichtquelle, von einem empirisch bestimmten Reflexionsfaktor (Materialkonstante) sowie der Oberflächenbeschaffenheit und vom Blickwinkel des Beobachters der Szene abhängig.
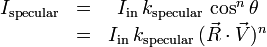
mit
- Iin ... Lichtstärke des einfallenden Lichtstrahls der Punktlichtquelle
- kspecular ... empirisch bestimmter Reflexionsfaktor für spiegelnde Komponente der Reflexion
- θ ... Winkel zwischen idealer Reflexionsrichtung des ausfallenden Lichtstrahls
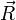 und Blickrichtung des Betrachters
und Blickrichtung des Betrachters 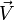
- n ... konstanter Faktor zur Beschreibung der Oberflächenbeschaffenheit (rau kleiner 32, glatt größer 32,
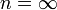 wäre ein perfekter Spiegel)
wäre ein perfekter Spiegel)
Vollständige Formel
Und hier die zusammengesetzte Formel für das Phong-Beleuchtungsmodell:
![\begin{matrix}
I_{\text{out}} & = & I_{\text{a}} \, k_{\text{ambient}} + I_{\text{in}} \, k_{\text{diffus}} \, \cos \phi + I_{\text{in}} \, k_{\text{specular}} \, \cos^n \theta \\
& = & I_{\text{a}} \, k_{\text{ambient}} + I_{\text{in}} \, ( k_{\text{diffus}} \, \cos \phi + k_{\text{specular}} \, \cos^n \theta ) \\
& = & I_{\text{a}} \, k_{\text{ambient}} + I_{\text{in}} \, \left[ k_{\text{diffus}} \, (\vec{L} \cdot \vec{N}) + k_{\text{specular}} \, (\vec{R} \cdot \vec{V})^n \right]
\end{matrix}](/pictures/dewiki/97/a8714173dcac48ade65ee37384720f0a.png)
mit
kambient + kdiffus + kspecular = 1
Siehe auch
Wikimedia Foundation.
