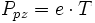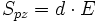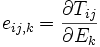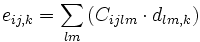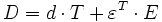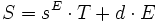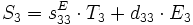Piezoelektrische Polarisation

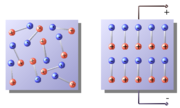
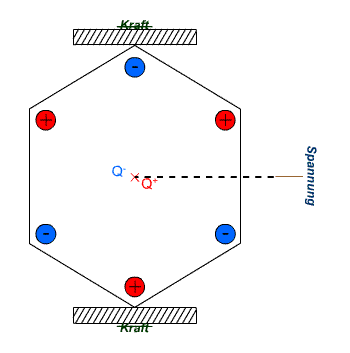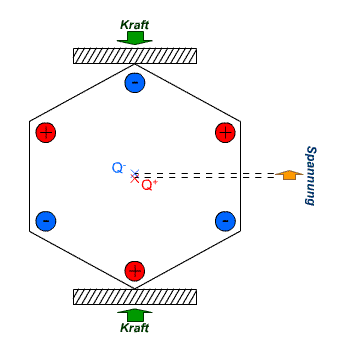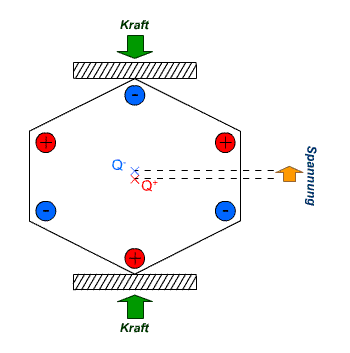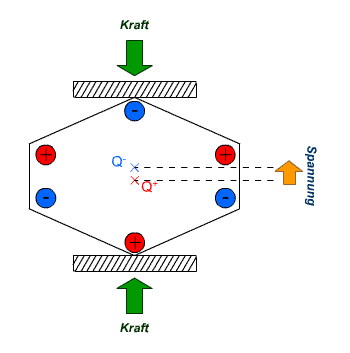Direkter Piezoeffekt: Durch mechanischen Druck verlagert sich der positive (Q+) und negative Ladungsschwerpunkt (Q–). Dadurch entsteht ein Dipol, bzw. eine elektrische Spannung am Element.

Piezoelektrizität (auch piezoelektrischer Effekt oder kurz: Piezoeffekt, veraltet: Piëzo-) beschreibt die Änderung der elektrischen Polarisation und somit das Auftreten einer elektrischen Spannung an Festkörpern, wenn sie elastisch verformt werden (direkter Piezoeffekt). Umgekehrt verformen sich Materialien bei Anlegen einer elektrischen Spannung (inverser Piezoeffekt).

Geschichte

Der direkte Piezoeffekt wurde im Jahre 1880 von den Brüdern Jacques und Pierre Curie entdeckt. Bei Versuchen mit Turmalinkristallen fanden sie heraus, dass bei mechanischer Verformung der Kristalle auf der Kristalloberfläche elektrische Ladungen entstehen, deren Menge sich proportional zur Beanspruchung verhält. Heute werden für Piezoelemente meist PZT-Keramiken (siehe Blei-Zirkonat-Titanat) benutzt.

Makroskopisch konnte der Effekt im Rahmen der Kontinuumsmechanik schon Anfang des 20. Jh. beschrieben werden, siehe dazu auch Berechnung. Die mikroskopische Beschreibung wurde erst durch ein tiefgehendes Verständnis der diskreten Struktur der kondensierten Materie möglich. Eine genauere mikroskopische Abhandlung wurde von Richard M. Martin 1972 gegeben.^[1].

Die ersten Anwendungen waren piezoelektrische Ultraschallwandler und bald darauf Schwingquarze für die Frequenzstabilisierung. Durch das 1950 an Walter P. Kistler erteilte Patent auf den Ladungsverstärker gelang der piezoelektrischen Messtechnik der Durchbruch zur breiten industriellen Anwendung.

Prinzip

Durch die gerichtete Verformung eines piezoelektrischen Materials bilden sich mikroskopische Dipole innerhalb der Elementarzellen (Verschiebung der Ladungs-Schwerpunkte). Die Aufsummierung über das damit verbundene elektrische Feld in allen Elementarzellen des Kristalls führt zu einer makroskopisch messbaren elektrischen Spannung. Gerichtete Verformung bedeutet, dass der angelegte Druck nicht von allen Seiten auf die Probe wirkt, sondern beispielsweise nur von gegenüberliegenden Seiten aus. Umgekehrt kann durch Anlegen einer elektrischen Spannung eine Verformung des Kristalls (bzw. des Bauteils aus Piezokeramik) erreicht werden.

Wie auch jeder andere Festkörper, können piezoelektrische Körper mechanische Schwingungen ausführen. Bei Piezoelektrika können diese Schwingungen einerseits elektrisch angeregt werden, bewirken andererseits auch wieder eine elektrische Spannung. Die Frequenz der Schwingung ist nur von der Schallgeschwindigkeit (eine Materialkonstante) und den Abmessungen des piezoelektrischen Körpers abhängig. Dadurch sind piezoelektrische Bauteile auch für Oszillatoren geeignet (z. B. Schwingquarze, siehe Anwendungen).

Piezoelektrische Materialien

Grundlagen

Der Piezoeffekt kann nur in nichtleitenden Materialien auftreten. Weiterhin sind alle nichtleitenden ferroelektrischen Materialien bzw. Materialien mit permanentem elektrischen Dipol auch piezoelektrisch, beispielsweise Bariumtitanat und Blei-Zirkonat-Titanat (PZT). Jedoch verhält sich nur ein Teil der Piezoelektrika ferroelektrisch.

Bei Kristallen ist die Kristallsymmetrie ein weiteres Kriterium für das Auftreten der Piezoelektrizität. Die piezoelektrische Polarisation tritt nicht auf, wenn der Kristall ein Inversionszentrum besitzt. Bei allen 21 nicht-zentrosymmetrischen Punktgruppen kann Piezoelektrizität auftreten, mit Ausnahme der kubischen Punktgruppe 432. Anders gesagt darf eine Elementarzelle kein Symmetriezentrum (= ein Punkt, an dem eine Punktspiegelung den Kristall in sich selbst überführt) besitzen.

Das bekannteste Material mit Piezoeigenschaften ist Quarz (SiO₂). Quarzkristalle besitzen die nicht-zentrosymmetrische Punktgruppe 32. Jedes Si-Atom sitzt in der Mitte eines Tetraeders aus vier Sauerstoffatomen. Eine in Richtung Grundfläche-Spitze (Kristallografische Richtung: [111]) wirkende Kraft verformt nun diese Tetraeder derart, dass die zusammengedrückten Tetraeder elektrisch polarisiert sind und so auf den Oberflächen des Kristalls (in [111]-Richtung) eine Nettospannung auftritt.

Technisch genutzte Materialien, die einen stärkeren Piezo-Effekt als Quarz zeigen, leiten sich oft von der Perowskit-Struktur ab, z. B.: Bariumtitanat (BaTiO₃). Die kubische Perowskit-Modifikation selbst besitzt die zentrosymmetrische Punktgruppe m3m und ist somit nicht-piezoelektrisch, das Material kann aber unterhalb einer kritischen Temperatur – die piezoelektrische Curie-Temperatur T_C – in eine nicht-zentrosymmetrische Perowskit-Struktur übergehen (rhomboedrisch/tetragonal, siehe Blei-Zirkonat-Titanat). Es zeigt dann eine spontane Polarisation und besitzt ferroelektrische Eigenschaften.

Piezoelektrische Kristalle

• Der wichtigste piezoelektrische Kristall ist Quarz, genauer gesagt die bis zu 573 °C stabile trigonale Kristallstruktur α-Quarz. Die wichtigste Anwendung sind Schwingquarze.
• Lithiumniobat hat gegenüber Quarz höhere piezoelektrische Konstanten und wird für piezoelektrische Filter und SAW-Bauelemente (surface acoustic wave Akustische Oberflächenwelle) verwendet.
• Galliumorthophosphat ist erst seit den 1990er Jahren als Piezoelektrikum erhältlich. Dieses Material ist dem Quarz ähnlich, hat jedoch höhere piezoelektrische Konstanten und eine bessere Temperaturstabilität. Es ist bis über 900 °C stabil.

Weitere piezoelektrische Kristalle sind Berlinit, Minerale der Turmalingruppe, Seignettesalz, und alle Ferroelektrika wie Bariumtitanat (BTO) oder Blei-Zirkonat-Titanat (PZT). BTO und PZT werden jedoch normalerweise nicht als Einkristalle, sondern in polykristalliner Form (Keramiken) verwendet.

Gegenüber piezoelektrischen Kristallen haben piezoelektrische Keramiken wie PZT den Vorteil wesentlich höherer piezoelektrischer Koeffizienten. Vorteile der Kristalle Quarz, Galliumorthophosphat und Lithiumniobat sind höhere Temperaturstabilität, geringere Verluste, eine wesentlich geringere Hysterese und kaum vorhandenes Kriechen (also verzögerte Verformung) nach Änderung der angelegten Spannung.

Piezoelektrische Keramiken

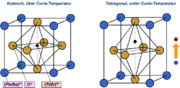Perowskit-Einheitszelle von Piezokeramiken. Unterhalb der Curie-Temperatur bildet sich ein Dipol aus.

Einprägen einer Polarisationsrichtung durch Ausrichtung der Dipole in einem elektrischen Feld

Industriell hergestellte Piezoelemente sind zumeist Keramiken. Diese Keramiken werden aus synthetischen, anorganischen, ferroelektrischen und polykristallinen Keramikwerkstoffen gefertigt. Typische Basismaterialien für Hochvolt-Aktoren sind modifizierte Blei-Zirkonat-Titanate (PZT) und für Niedervolt-Aktoren Blei-Magnesium-Niobate (PMN).

Der Stoffverbund der PZT-Keramiken (Pb, O, Ti/Zr) kristallisiert in der Perowskit-Kristallstruktur; unterhalb der piezoelektrischen Curietemperatur bildet sich durch Verzerrungen der idealen Perowskit-Struktur ein Dipolmoment aus. Bei keramischen Piezoelementen sind die internen Dipole nach dem Sinterprozess noch ungeordnet, weshalb sich keine piezoelektrischen Eigenschaften zeigen. Die Weissschen Bezirke oder Domänen besitzen eine willkürliche räumliche Orientierung und gleichen sich gegenseitig aus. Eine deutlich messbare piezoelektrische Eigenschaft lässt sich erst durch ein äußeres elektrisches Gleichfeld aufprägen (einige 10⁶ V/m), während das Material bis knapp unter die Curie-Temperatur erwärmt und wieder abgekühlt wird. Die eingeprägte Orientierung bleibt danach zum großen Teil erhalten (remanente Polarisation) und wird als Polarisationsrichtung bezeichnet.

Das Drehen der Weissschen Bezirke durch die Polarisation führt zu einer leichten Verzerrung des Materials sowie einer makroskopischen Längenzunahme in Polarisationsrichtung.

Weitere piezoelektrische Materialien

Als aktive Sensormaterialien werden zunehmend auch piezoelektrische Dünnschichten eingesetzt. Mit Hilfe von Halbleitertechnologien ist es möglich, diese aktiven piezoelektrischen Dünnschichten auf Silizium abzuscheiden. Hierbei handelt es sich meist um Zinkoxid (ZnO) oder Aluminiumnitrid (AlN).

Der Kunststoff Polyvinylidenfluorid (PVDF) lässt sich – ähnlich wie piezoelektrische Keramiken – polarisieren und ist dann piezoelektrisch. Anwendungen hierfür sind z. B. Hydrophone.

Berechnung

Im Folgenden wird die makroskopische Beschreibung im Rahmen der Kontinuumsmechanik gezeigt. Es wird nur eine lineare Näherung zwischen den betrachteten Größen berücksichtigt. Nichtlineare Effekte wie die Elektrostriktion werden vernachlässigt.

Geometrie

Definition der Achsenrichtungen

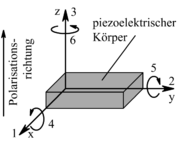
Zur Beschreibung der räumlich unterschiedlichen Eigenschaften wird ein Koordinatensystem gewählt. Für die Indizierung wird üblicherweise ein x-, y-, z-Koordinatensystem verwendet, dessen Achsen man mit den Ziffern 1, 2, 3 bezeichnet (Achse 3 entspricht der Polarisationsachse). Die Scherungen an diesen Achsen tragen die Ziffern 4, 5, 6. Basierend auf diesen Achsen werden die piezoelektrischen Eigenschaften mit Tensoren in Gleichungen gefasst.

Gleichungen

Die einfachsten Gleichungen für den Piezoeffekt beinhalten die Polarisation P_pz (Einheit [C/m²]) und die Verformung S_pz (Dimensionslose Größe):

$P_{pz} = e\cdot T$

$S_{pz} = d\cdot E$

wobei d,e die piezoelektrischen Koeffizienten, E die elektrische Feldstärke (V/m) und T die mechanische Spannung (N/m²) angibt. Die erste Gleichung beschreibt den direkten, die zweite den inversen Piezoeffekt.

Die piezoelektrischen Koeffizienten sind:

• piezoelektrische Verzerrungskoeffizienten (Reaktion der Verzerrung auf das elektrische Feld)

$d_{ij,k} = \frac{\partial \epsilon_{ij}}{\partial E_k}$

• piezoelektrische Spannungskoeffizienten (Reaktion der mechanischen Spannung auf das elektrische Feld)

$e_{ij,k} = \frac{\partial T_{ij}}{\partial E_k}$

Die beiden Koeffizienten sind über die elastischen Konstanten in einen Zusammenhang zu bringen:

$e_{ij,k} = \sum_{lm} \left( C_{ijlm} \cdot d_{lm,k} \right)$

Effekte zweiter Ordnung (inverser Piezoeffekt) werden durch die elektrostriktiven Koeffizienten beschrieben.

Verkoppelungsmatrix

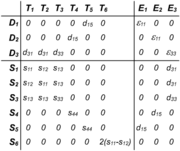
Die oben angegebenen Tensoren werden normalerweise in Matrixform umgeschrieben (Voigtsche Notation). Damit erhält man Matrizen mit sechswertigen Komponenten, welche der oben dargestellten Achsendefinition entsprechen. Die piezoelektrischen Effekte werden dann mittels zweier gekoppelter Gleichungen beschrieben, in der die dielektrische Verschiebung D anstelle der Polarisation verwendet wird.

$D = d\cdot T + \varepsilon^T\cdot E$

$S = s^E\cdot T + d \cdot E$

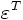$\varepsilon^T$ Permittivität bei konstanter mechanischer Spannung

s^E Elastizitätskonstante bei konstanter elektrischer Feldstärke

Es ist gebräuchlich, die Elemente dieser Gleichungen in der Verkoppelungsmatrix zusammenzufassen.

Wichtigster Materialparameter für den inversen Piezoeffekt und damit für Aktoren ist die piezoelektrische Ladungskonstante d. Sie beschreibt den funktionalen Zusammenhang zwischen der angelegten elektrischen Feldstärke und der damit erzeugten Dehnung. Die charakteristischen Größen eines piezoelektrischen Wandlers sind für die verschiedenen Wirkrichtungen unterschiedlich.

Links: Quereffekt. Rechts: Längseffekt

Im Bereich der Aktorik sind zwei Haupteffekte relevant. Für diese beiden Effekte vereinfacht sich die Gleichung für die Ausdehnung wie folgt:

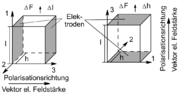
Piezoelektrischer Quer- oder Transversaleffekt (d₃₁-Effekt). Die mechanische Kraft wirkt quer zum angelegten Feld.

$S_1 = s_{11}^E \cdot T_1 + d_{31}\cdot E_3$

Piezoelektrischer Längs- oder Longitudinaleffekt (d₃₃-Effekt). Die mechanische Kraft wirkt parallel zum angelegten Feld.

$S_3 = s_{33}^E \cdot T_3 + d_{33}\cdot E_3$

Anwendungen

Generell lassen sich die Anwendungen in drei Bereiche aufteilen:

Sensorik

Das Auftreten der piezoelektrischen Ladung bei mechanischer Verformung wird bei Kraft-, Druck- und Beschleunigungssensoren genutzt. Die dabei entstehende Ladung kann mit einem Ladungsverstärker in eine elektrische Spannung mit niedriger Quellimpedanz umgewandelt werden. Bei der anderen Möglichkeit, mit dieser Ladung einen Kondensator aufzuladen und dessen Spannung mit einem möglichst hochohmigen Voltmeter zu messen, können mangelhafte Isolationswiderstände beispielsweise durch Feuchtigkeit das Ergebnis stark verfälschen und die Registrierung langsamer Veformungen verhindern.

Piezoelement zur Wandlung von mechanischem Druck in elektrische Spannung.

• In der Musik werden Piezoelemente als Tonabnehmer für akustische Instrumente genutzt, hauptsächlich bei Saiteninstrumenten wie Gitarre, Geige oder Mandoline. Die dynamische Verformung des Instrumentes (Vibration des Klangkörpers) wird in eine geringe Wechselspannung umgewandelt, die dann elektrisch verstärkt wird.
• Bei piezoelektrischen Beschleunigungssensoren bzw. -aufnehmern kommt es bei einer mechanischen Deformation (Kompression oder Scherung) durch die Beschleunigung zu einer Ladungstrennung und damit zu einer abgreifbaren Ladung (bzw. Spannung) an den aufgedampften Elektroden.
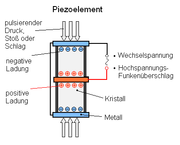
• In einem Piezofeuerzeug wird in einem Piezozünder ein plötzlicher großer Druck (Hammer) verwendet, um eine kurzzeitige hohe elektrische Spannung zu erzeugen. Der Funkenüberschlag zündet dann die Gasflamme.
• Bei Schwingquarzen kann der Einfluss verschiedener Größen auf die Resonanzfrequenz, bei akustischen Oberflächenwellenbauteilen der Einfluss auf die Verzögerungszeit ausgenutzt werden. Eine wichtige Anwendung ist die Messung der auf dem Quarz aufgebrachten Masse, z. B. bei industriellen Beschichtungsverfahren zur Bestimmung der Schichtdicke. Es kann auch die Temperaturabhängigkeit der Schwingungsfrequenz gemessen werden; solche Schwingquarzthermometer sind jedoch nicht mehr im Handel.

Aktorik

Piezoaktoren können nach zwei unterschiedlichen Kriterien unterschieden werden. Der Betriebsweise (quasistatischer , oder Resonanzbetrieb) oder nach der Richtung des genutzten Effekts. Da Quer- und Längseffekt gleichzeitig auftreten wird nach dem genutzen Effekt unterschieden.

Aus der Unterscheidung Transversaleffekt (Quereffekt) und Longitudinaleffekt (Längseffekt) ergeben sich drei verschiedene Grundelemente für piezoelektrische Aktoren: der Dickenschwinger, das Querdehnelement und als besondere Bauform der Biegeschwinger (Bimorph). Dieser ist eine Kombination aus zwei Querdehnelementen. Eine entgegengesetzte Ansteuerung der Elemente bewirkt hier eine Verbiegung des Aktors, weshalb er eine eigenständige Bezeichnung erhält.

Piezoaktorische Grundelemente

Über den Quer- und Längseffekt hinaus kann der Piezo durch Anlegen des elektrischen Feldes senkrecht zur Polarisationsrichtung auch eine Scherung_(Mechanik) erfahren. Dieser Effekt wird jedoch meist nur in akustischen Wandlern und Beschleunigungssensoren genutzt.

Piezo-Lautsprecher

In die Kategorie quasistatischer Betrieb fallen auch Aktoren, die im kHz Bereich betrieben werden, solange der Resonanzfall nicht eintritt. Die hohe Genauigkeit und die große Dynamik prädestinieren den Piezoaktor auch für Positionieraufgaben und zur aktiven Schwingungsdämpfung. Durch den Einsatz gestapelter Piezoelemente oder durch Hebel lassen sich die relativ kurzen Stellwege von Δl/l = 10⁻³ verlängern. Begrenzend auf die Stellwege wirken die Spannungsfestigkeit des Materials, die hohen Betriebsspannungen und die in eine Sättigung laufende Kennlinie des Materials. Typische Längenänderungen liegen bei Niedervoltelementen bei 0,1 µm, bei Hochvoltelemten bei ca. 1 µm. Sollen größere Stellwege bewältigt werden bietet sich der Resonanzbetrieb an.

Im Resonanzbetrieb wird der Rotor der Motors vom Piezo durch eine Wanderwelle angetrieben. Zusätzlich wird die Massenträgheit des Rotors genutzt um eine kontinuierliche Bewegung zu erzeugen. Damit lassen sich auch größere Stellwege bewältigen, wie z. B. in einem Objektiv (Optik).

Als Beispiele für die quasistatische Anwendung von Piezoaktoren seien genannt: Braillezeilen für Blinde bei denen durch Anlegen einer Spannung für den Blinden tastbare Stifte hochgedrückt werden, womit am PC der Monitortext in tastbare Blindenschriftzeichen umgesetzt wird.

Klassische Beispiele für diese Betriebsform dürften Tintendrucker (engl. Drop-on-Demand, z. B. von Epson) und Piezolautsprecher sein, bei denen die Schallwellen durch eine tonfrequente Wechselspannung erzeugt werden. Auch Dieseleinspritzsysteme arbeiten mit piezoelektrischen Aktoren (keramische Vielschichtbauteile mit Edelmetallinnenelektroden) und haben die Common-Rail-Technik verbessert. Dabei wird die Einspritzung von Diesel über Ventile teilweise ersetzt. Seit 2005 werden auch beim Pumpe-Düse-System Piezoaktoren eingesetzt. Industrieunternehmen, die derartige Piezoaktoren in großen Stückzahlen fertigen, sind die Firmen Epcos und Bosch.

Die Polarisation des Piezoelements legt die Raumrichtungen im Piezoelement fest. Damit sind auch die richtungsabhängigen piezoelektrischen Ladungskonstanten vorgegeben. Typischer Weise gilt: d_longitudinal = −0,5 · d_transversal. Für zwei- oder dreidimensionale Bewegungen müssen mehrere Piezo-Elemente so kombiniert werden, dass sie in verschiedene Richtungen wirken.

Elektrische Bauelemente

Bei diesen Anwendungen wird eine mechanische Schwingung eines piezoelektrischen Festkörpers elektrisch angeregt und wieder elektrisch detektiert. Es wird grundlegend zwischen zwei Typen unterschieden:

• Volumenresonatoren, bei denen im Wesentlichen das gesamte piezoelektrische Element schwingt. Die wichtigsten Vertreter sind Schwingquarze und keramische Filter.
• SAW-Bauelemente basieren auf akustischen Oberflächenwellen (engl. surface acoustic wave, SAW). Beispiele sind SAW-Filter und -Verzögerungsleitungen.

Weitere Anwendungen

Dieser Artikel oder Abschnitt besteht hauptsächlich aus Listen, an deren Stelle besser Fließtext stehen sollte.

Der Effekt findet Verwendung in:

• Piezofeuerzeugen zur Erzeugung des Zündfunkens
• Piezomikrofonen (Kristallmikrofon)
• Buzzern (Summern)
• manchen Kopfhörern

• mikromechanischen Sensoren
  • Beschleunigungssensoren
  • Drehratensensoren
  • Drucksensoren: beispielsweise als in die Fahrbahn eingelassener Sensor zur Verkehrsüberwachung (in Kombination mit den so genannten „Starenkasten“)
  • Kraftsensoren
  • Quarzmikrowaagen
  • Ultraschallsensoren zur Erzeugung und Detektion von mechanischen Schwingungen für Durchfluss- und Füllstandsmessung (Prozessmesstechnik)
  • Schallköpfen von Ultraschallgeräten (Ultraschalldiagnosegeräten), zur Erzeugung und Detektion von mechanischen Schwingungen, früher auch in Fernbedienungen
  • Klopfsensoren im Pkw
  • Ultraschallprüfköpfen zur Erzeugung und Detektion von mechanischen Schwingungen für die zerstörungsfreie Werkstoffprüfung

• mikromechanischen Aktoren
  • Piezomotoren (Squiggler)
  • Ultraschallmotoren, z. B. für die Objektivautofokussierung oder Uhrenantrieben
  • in Mikro- und Nanopositioniersystemen
    • Rastertunnelmikroskopen
    • Rasterelektronenmikroskopen
    • Rasterkraftmikroskopen
    • Michelson-Interferometern
  • in der Ventiltechnik
    • Proportional-Druckregler
    • Einspritzdüsen von Pkw (Serienstart 2000 für Dieselmotoren)
    • Druckköpfen von Tintenstrahldruckern

• Tonabnehmern
• elektroakustischen Verzögerungsleitungen wie beispielsweise in älteren PAL- oder SECAM-Farbfernsehgeräten
• Batterieloser Funktechnik (Schaltern)
• optischen Modulatoren
• Zuführtechnik

Einzelnachweise

1. ↑ Richard M. Martin: Piezoelectricity. In: Physical Review B. 5, Nr. 4, 1972, S. 1607–1613 (doi:10.1103/PhysRevB.5.1607). 

Siehe auch

• Pyroelektrizität
• Piezoresistiver Effekt

Weblinks

• Der Piezoeffekt bei Kristallen
• „Piezofibel“ von piezosystem jena (PDF)
• 'Vielschicht-Piezoaktoren' – Fortschritte bei Fertigung und Lebensdauer von Multilayeraktoren (PDF engl.)
• Piezo-Tutorium – Piezoaktorik in der Präzisionsstelltechnik
• Materialeingeschaften (engl.)

Video

[1] Simulation,Motor aus mehreren Elementen (Mikroschrittbetrieb)