- Planck'sches Strahlungsgesetz
-
Das plancksche Strahlungsgesetz beschreibt die Intensitätsverteilung der elektromagnetischen Energie und Leistung bzw. die Dichteverteilung aller Photonen in Abhängigkeit von Wellenlänge bzw. Frequenz, die von einem schwarzen Körper – einer idealen Strahlungsquelle – bei einer bestimmten Temperatur abgestrahlt werden.
Bei der Herleitung des Strahlungsgesetzes durch Max Planck im Jahr 1900 zeigte sich, dass eine Beschreibung im Rahmen der klassischen Physik nicht möglich ist[1]. Vielmehr erwies es sich als notwendig, ein neues Postulat einzuführen, demzufolge der Energieaustausch zwischen Oszillatoren und dem elektromagnetischen Strahlungsfeld nicht kontinuierlich, sondern in Form kleinster Energiepakete (später als Quanten bezeichnet) stattfindet. Plancks Herleitung des Strahlungsgesetzes gilt daher heute als die Geburtsstunde der Quantenphysik und wird den alten Quantentheorien zugerechnet.
Inhaltsverzeichnis
Grundlagen und Bedeutung
Nach dem kirchhoffschen Strahlungsgesetz sind für jeden Körper bei jeder Wellenlänge das Absorptionsvermögen und das Emissionsvermögen für thermische Strahlung proportional zueinander. Ein Schwarzer Körper ist ein hypothetischer Körper, der bei jeder Wellenlänge die auf ihn treffende Strahlung vollständig absorbiert. Da sein Absorptionsvermögen bei jeder Wellenlänge den größtmöglichen Wert annimmt, nimmt auch sein Emissionsvermögen bei allen Wellenlängen den maximal möglichen Wert an. Ein realer Körper kann bei keiner Wellenlänge mehr thermische Strahlung aussenden als ein Schwarzer Körper, der daher eine ideale thermische Strahlungsquelle darstellt. Da das Spektrum des Schwarzen Körpers außerdem von keinen anderen Parametern als der Temperatur abhängt, insbesondere von keinen Materialeigenschaften, stellt er eine für zahlreiche Zwecke nützliche Referenzquelle dar.
Neben der erheblichen praktischen Bedeutung des Schwarzen Körpers gilt die Entdeckung des planckschen Strahlungsgesetzes im Jahre 1900 gleichzeitig als Geburtsstunde der Quantenphysik, da Planck zur Erklärung der zunächst empirisch gefundenen Formel annehmen musste, dass Licht (bzw. elektromagnetische Strahlung im Allgemeinen) nicht kontinuierlich, sondern nur diskret in Quanten (heute spricht man von Photonen) aufgenommen und abgegeben wird.
Weiterhin vereinigte und bestätigte das plancksche Strahlungsgesetz Gesetzmäßigkeiten, die schon vor seiner Entdeckung teils empirisch, teils aufgrund thermodynamischer Überlegungen gefunden worden waren:
- das Stefan-Boltzmann-Gesetz, welches die gesamte abgestrahlte Leistung eines Schwarzen Körpers (proportional zu T4) angibt.
- das Rayleigh-Jeans-Gesetz, das die spektrale Energieverteilung für lange Wellenlängen beschreibt.
- das wiensche Strahlungsgesetz, das die spektrale Energieverteilung für kurze Wellenlängen wiedergibt.
- das wiensche Verschiebungsgesetz, das Wilhelm Wien (1864–1928) 1893 formulierte, welches den Zusammenhang zwischen Emissionsmaximum eines Schwarzen Körpers und seiner Temperatur herstellt.
Herleitung und Historie
Man betrachte als vereinfachtes Beispiel einen kubusförmigen Hohlraum der Seitenlänge L und des Volumens V, welcher elektromagnetische Hohlraumstrahlung im thermischen Gleichgewicht enthält. Im Gleichgewicht können sich nur stehende Wellen ausbilden; die erlaubten Wellen können in eine beliebige Richtung laufen, müssen dabei jedoch die Bedingung erfüllen, dass zwischen zwei gegenüberliegende Hohlraumflächen jeweils eine ganzzahlige Anzahl von Halbwellen passt. Das hat folgenden Grund: Da die elektromagnetischen Wellen innerhalb der Wände des Hohlraums nicht existieren können, ist hier die elektrische und magnetische Feldstärke null. Damit müssen sich die Knotenpunkte der Wellen in den Wänden befinden. Es sind also nur bestimmte diskrete Schwingungszustände erlaubt; die gesamte Hohlraumstrahlung setzt sich aus diesen stehenden Wellen zusammen.
Die Zustandsdichte
Die Anzahl erlaubter Schwingungszustände nimmt bei höheren Frequenzen zu, weil es für Wellen mit kürzerer Wellenlänge mehr Möglichkeiten gibt, sich so in den Hohlraum einzupassen, dass die Ganzzahligkeitsbedingungen für ihre Komponenten in x-, y- und z-Richtung erfüllt sind. Die Anzahl dieser erlaubten Schwingungszustände im Frequenzintervall zwischen ν und ν + dν und pro Volumeneinheit heißt Zustandsdichte
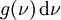 und errechnet sich zu
und errechnet sich zu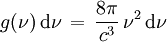 .
.Die Ultraviolett-Katastrophe
Nun fasst man jeden dieser Schwingungszustände je Frequenzintervall als harmonische Oszillatoren der Frequenz ν auf. Wenn alle Oszillatoren im thermischen Gleichgewicht bei der Temperatur T schwingen, dann wären nach dem Gleichverteilungssatz der klassischen Thermodynamik zu erwarten, dass jeder dieser Oszillatoren im Mittel die kinetische Energie kT/2 und die potentielle Energie kT/2, also insgesamt die Energie kT trägt. Die Energiedichte der Hohlraumstrahlung im Frequenzintervall zwischen ν und ν + dν wäre demnach das Produkt der Zustandsdichte der erlaubten Schwingungszustände
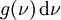 und der mittleren Energie je klassischem Schwingungszustand kT, also
und der mittleren Energie je klassischem Schwingungszustand kT, also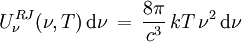 .
.Dies ist das Strahlungsgesetz nach Rayleigh-Jeans. Es gibt die tatsächlich gemessene Energiedichte bei niedrigen Frequenzen gut wieder, sagt aber fälschlich eine mit höheren Frequenzen stets quadratisch wachsende Energiedichte voraus, sodass der Hohlraum über alle Frequenzen integriert eine unendliche Energiedichte enthalten müsste (Ultraviolett-Katastrophe[2]). Das Problem ist: Jeder vorhandene Schwingungszustand trägt zwar im Mittel nur die Energie kT, aber es sind unendlich viele solcher Schwingungszustände angeregt.
Die empirische Lösung
Planck stützte sich bei seiner Herleitung des Strahlungsgesetzes nicht auf den Rayleighschen Ansatz, vielmehr ging er von der Entropie aus und fügte in die Gleichungen probeweise verschiedene Zusatzterme ein, die nach dem damaligen Physikkenntnissen zwar unverständlich waren - ihnen aber auch nicht widersprachen. Besonders einfach war ein Zusatzterm, der zu einer Formel führte, die die schon gemessenen Spektralkurven sehr gut beschrieb (1900) [3]. Damit blieb diese Formel reine Empirie – aber sie beschrieb die bekannten experimentellen Messungen über das gesamte Frequenzspektrum korrekt. Planck gab sich damit aber nicht zufrieden. Es gelang ihm, die Strahlungskonstanten C und c aus der wienschen Formel durch Naturkonstanten zu ersetzen, nur ein Faktor h („hilf“) blieb übrig.
Die Quantenhypothese
Ausgehend von der verbesserten empirischen Strahlungsformel kam Planck innerhalb weniger Monate zu einem epochemachenden Ergebnis, es war die Geburtsstunde der Quantenphysik: Er musste sich selbst gegen seine eigene Überzeugung eingestehen, dass die Energieabgabe nicht kontinuierlich erfolgt, sondern nur in Vielfachen von kleinsten "h"-Einheiten, die ihm zu Ehren dann später als Plancksches Wirkungsquantum bezeichnet wurde. Nach dieser von Planck eingeführten Quantenhypothese kann ein Oszillator der Frequenz ν anstelle beliebiger Energiemengen nur ganzzahlige Vielfache der Energie hν aufnehmen; insbesondere bedarf er einer Mindestenergie hν, um überhaupt angeregt zu werden. Schwingungszustände, deren Mindestenergie hν deutlich über der thermisch zur Verfügung gestellten Energie kT liegen, können nicht angeregt werden, sie bleiben eingefroren. Jene Schwingungszustände, deren Mindestenergie nur wenig über kT liegt, können mit gewisser Wahrscheinlichkeit angeregt werden, so dass von ihnen ein bestimmter Bruchteil zur gesamten Hohlraumstrahlung beiträgt. Lediglich Schwingungszustände mit niedriger Mindestenergie hν, also kleineren Frequenzen, können die angebotene thermische Energie vollständig aufnehmen und werden (im Mittel) mit Sicherheit angeregt.
Quantisierte Schwingungszustände
Die statistische Thermodynamik zeigt, dass durch Anwendung von Quantenhypothese und Boltzmann-Statistik ein Schwingungszustand der Frequenz ν im Mittel folgende Energie trägt:
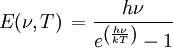
Gemäß diesem Zusammenhang wird nun vermieden, dass die höherfrequenten elektromagnetischen Schwingungszustände, die nach geometrischen Kriterien durchaus im Hohlraum existieren könnten, wegen ihrer hohen Anregungsschwelle durch die zur Verfügung stehende thermische Energie nicht angeregt werden können und daher nicht zur Energiedichte im Hohlraum beitragen.
Das Strahlungsgesetz
Das Produkt der Zustandsdichte der erlaubten Schwingungszustände
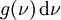 und der mittleren Energie je quantisiertem Schwingungszustand
und der mittleren Energie je quantisiertem Schwingungszustand 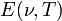 ergibt dann bereits die plancksche Energiedichte
ergibt dann bereits die plancksche Energiedichte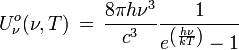 .
.Weil die mittlere Energie bei hohen Frequenzen stärker abnimmt als die Zustandsdichte anwächst, nimmt die spektrale Energiedichte - als deren Produkt - zu höheren Frequenzen hin wieder ab - nachdem sie ein Maximum durchlaufen hat - und die Gesamtenergiedichte bleibt endlich. So erklärte Planck mittels seiner Quantenthese, warum die aus Grundlage der klassischen Thermodynamik vorausgesagte Ultraviolett-Katastrophe in Wirklichkeit nicht stattfindet.
Wichtige Anwendungen des Strahlungsgesetzes
Das plancksche Strahlungsgesetz wird in verschiedenen Formelvarianten dargestellt, die Größen für Intensitäten, Flussdichten und Spektralverteilungen verwenden, welche für die betrachteten Sachverhalte zweckmäßig sind. Alle Formen der unterschiedlichen Strahlungsgrößen sind lediglich unterschiedliche Formen des einen Gesetzes.
Ausstrahlung
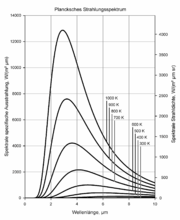
Das erste nebenstehende Bild zeigt Plancksche Strahlungsspektren für verschiedene Temperaturen zwischen 300 K und 1000 K in linearer Darstellung. Man erkennt die typische Glockenform mit einem deutlich ausgeprägten Strahlungsmaximum, einem steilen Abfall zu kurzen Wellenlängen hin und einem länger auslaufenden Abfall zu großen Wellenlängen hin. Die Lage des Strahlungsmaximums verschiebt sich, wie es das wiensche Verschiebungsgesetz verlangt, mit zunehmender Temperatur zu kürzeren Wellenlängen. Gleichzeitig nimmt gemäß dem Stefan-Boltzmann-Gesetz die gesamte spezifische Ausstrahlung (sie entspricht der Fläche unter der jeweiligen Kurve für die spektrale spezifische Ausstrahlung) mit der vierten Potenz der absoluten Temperatur zu. Dieses überproportionale Anwachsen der Strahlungsintensität mit steigender Temperatur macht es schwierig, Kurven über einen größeren Temperaturbereich in einem Diagramm darzustellen.
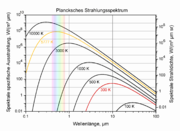
Das zweite Bild verwendet daher für beide Achsen eine logarithmische Unterteilung. Dargestellt sind hier Spektren für Temperaturen zwischen 100 K und 10000 K.
Rot hervorgehoben ist die Kurve für 300 K, was typischen Umgebungstemperaturen entspricht. Das Maximum dieser Kurve liegt bei 10 μm; im Bereich um diese Wellenlänge, dem langwelligen Infrarot, findet also der Strahlungsaustausch von Objekten auf Raumtemperatur statt. Typische Infrarotthermometer und Thermografiekameras arbeiten in diesem Bereich.
Die Kurve für 3000 K entspricht dem typischen Strahlungsspektrum einer Glühlampe. Nun wird bereits ein Teil der emittierten Strahlung im schematisch angedeuteten sichtbaren Spektralbereich abgegeben. Das Strahlungsmaximum liegt jedoch noch im nahen Infrarot.
Gelb hervorgehoben ist die Kurve für 5777 K, die Effektivtemperatur der Sonne. Das Strahlungsmaximum liegt nun mitten im sichtbaren Spektralbereich. Die von der Sonne thermisch ausgestrahlte UV-Strahlung wird glücklicherweise zum größten Teil von der Ozonschicht der Erdatmosphäre ausgefiltert.
Einstrahlung
Wie dem Diagramm zu entnehmen ist, liegt die spektrale spezifische Ausstrahlung der Sonne für alle Wellenlängen deutlich über der Ausstrahlung von terrestrischen Gegenständen mit T ≈ 300 K. Bei einer Wellenlänge von 10 μm strahlt beispielsweise ein Quadratmeter Sonnenoberfläche etwa 400mal so stark wie ein Quadratmeter Hausfassade. Dies bedeutet jedoch nicht, dass die uns umgebende Wärmestrahlung überwiegend von der Sonne stammt. Für die auf einen Quadratmeter Empfängerfläche bezogene spektrale Bestrahlungsstärke ist die spektrale Strahldichte der Sendefläche mit dem Raumwinkel Ω zu multiplizieren, den diese Fläche vom Empfänger aus gesehen einnimmt. Die Sonne stellt für einen irdischen Empfänger eine sehr kleine Quelle dar (Ω = 6,8·10-5 sr). Vergleicht man sie z.B. mit einem 300 K warmen terrestrischen Objekt, welches das Gesichtsfeld des Empfängers zur Hälfte ausfüllt (Ω = 3,14 sr), so ist die Bestrahlungsstärke der Sonne bei λ = 10 μm um den Faktor 400·(6,8·10-5 / 3,14) ≈ 1/100 geringer, also praktisch vernachlässigbar. Dazu kommen noch die Absorption eines Teils der solaren Wärmestrahlung durch die Atmosphäre und eine weitere Reduktion bei nicht senkrechter Bestrahlung der Empfängerfläche.
Häufig gebrauchte Formeln und Einheiten
Für die mathematische Darstellung des Gesetzes existieren zahlreiche verschiedene Varianten, je nachdem ob das Gesetz in Abhängigkeit von der Frequenz oder der Wellenlänge formuliert werden soll, ob die Intensität der Strahlung in eine bestimmte Richtung oder die Abstrahlung in den gesamten Halbraum betrachtet werden soll, ob Strahlgrößen, Energiedichten oder Photonenzahlen beschrieben werden sollen. Diese verschiedenen Formen werden in der Formelsammlung plancksches Strahlungsgesetz in ihrem gegenseitigen Zusammenhang ausführlich dargestellt und erläutert.
Häufig gebraucht wird die Formel für die spektrale spezifische Ausstrahlung
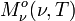 eines Schwarzen Körpers der absoluten Temperatur T. Für sie gilt
eines Schwarzen Körpers der absoluten Temperatur T. Für sie giltin der Frequenzdarstellung:
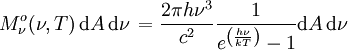
SI-Einheit von 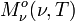 : W m-2 Hz-1
: W m-2 Hz-1und in der Wellenlängendarstellung:
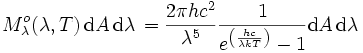
SI-Einheit von 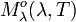 : W m-2 μm-1.
: W m-2 μm-1.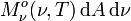 ist die Strahlungsleistung, die vom Flächenelement dA im Frequenzbereich zwischen ν und ν + dν in den gesamten Halbraum abgestrahlt wird. Weiter sind h das plancksche Wirkungsquantum, c die Lichtgeschwindigkeit und k die Boltzmannkonstante.
ist die Strahlungsleistung, die vom Flächenelement dA im Frequenzbereich zwischen ν und ν + dν in den gesamten Halbraum abgestrahlt wird. Weiter sind h das plancksche Wirkungsquantum, c die Lichtgeschwindigkeit und k die Boltzmannkonstante.Bei der Umrechnung zwischen Frequenz- und Wellenlängendarstellung ist zu beachten, dass wegen
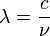 gilt:
gilt: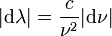 und
und 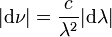
Einzelnachweise
- ↑ M. Planck: „Zur Theorie des Gesetzes der Energieverteilung im Normalspektrum“, Verhandlungen der Deutschen physikalischen Gesellschaft 2(1900) Nr. 17, S. 245, Berlin (vorgetragen am 14. Dezember 1900) Onlinedokument (engl. Übersetzung)
- ↑ Entgegen häufig zu findenden Darstellungen spielten das Rayleigh-Jeans-Gesetz und die Ultraviolett-Katastrophe keine Rolle bei Plancks Entdeckung des Strahlungsgesetzes. Die physikalisch unsinnige Divergenz des Rayleigh-Jeans-Gesetzes bei hohen Strahlungsfrequenzen wurde erstmals im Jahr 1905 (unabhängig voneinander) von Einstein, Rayleigh und Jeans beschrieben. Der Begriff „Ultraviolett-Katastrophe“ wurde erstmals 1911 von Paul Ehrenfest verwendet: Ehrenfest, “Welche Züge der Lichtquantenhypothese spielen in der Theorie der Wärmestrahlung eine wesentliche Rolle?” Annalen der Physik, vol. 341, issue 11 (1911), 91–118.
- ↑ D. Giulini, N. Straumann: „… ich dachte mir nicht viel dabei …“ Plancks ungerader Weg zur Strahlungsformel, Oktober 2000 arXiv:quant-ph/0010008.
Literatur
- Baehr, H.D., Stephan, K.: Wärme- und Stoffübertragung, 4. Auflage. Springer-Verlag, Berlin 2004, ISBN 3-540-40130-X; Kap. 5: Wärmestrahlung
Siehe auch
- Grauer Körper
- Glut (Lichtausstrahlung)
- Strahlungsaustausch
- Zur historischen Entwicklung siehe auch: Max Planck
Weblinks
- Plancks Strahlungsformel
- Zur Geschichte der Entdeckung der Strahlungsgesetze
- Ableitung der planckschen Strahlungsformel nach Einstein (Universität Ulm)
- WEBGEO-Modul: Physik der Wärmestrahlung – WEBGEO - E-Learning-Portal für Geographie und Nachbarwissenschaften
Wikimedia Foundation.