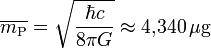- Planckdichte
-
Die Planck-Einheiten, benannt nach Max Planck, bilden ein natürliches Einheitensystem. Sie werden aus drei Naturkonstanten hergeleitet, nämlich der Gravitationskonstanten G, der Vakuumlichtgeschwindigkeit c und dem planckschen Wirkungsquantum h und markieren eine Grenze der Anwendbarkeit der bekannten Naturgesetze (siehe Planck-Skala).
Inhaltsverzeichnis
Allgemeines
Ein System „natürlicher Einheiten“ beruht darauf, dass z.B. für Zeit und Länge nicht zwei verschiedene Maßeinheiten gebraucht werden, da eine natürliche Äquivalenz, in diesem Fall durch die Lichtausbreitung besteht. Auch das SI-Einheitensystem benutzt seit 1983 die Vakuum-Lichtgeschwindigkeit zur Definition des Meter, indem es den Wert der Vakuum-Lichtgeschwindigkeit zu 299.792.458 m/s festsetzt. Durch die Weiterverwendung getrennter Maßeinheiten und dieses Zahlenwerts bleibt es aber in der Tradition älterer Maßsysteme. Setzt man hingegen die Vakuum-Lichtgeschwindigkeit zu 1, vereinfachen sich die grundlegenden physikalischen Formeln, jedoch werden die Bedürfnisse des täglichen Lebens für leicht handhabbare Einheiten schlechter erfüllt.
In der Quantenphysik werden oft die Lichtgeschwindigkeit c und das Plancksche Wirkungsquantum
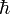 zu 1 gesetzt, wodurch nur eine Maßeinheit übrig bleibt. Durch die entsprechende Umrechnung lassen sich dann Längen, Zeiten, Energien und Massen sämtlich z.B. in eV ausdrücken.
zu 1 gesetzt, wodurch nur eine Maßeinheit übrig bleibt. Durch die entsprechende Umrechnung lassen sich dann Längen, Zeiten, Energien und Massen sämtlich z.B. in eV ausdrücken.In der allgemeinen Relativitätstheorie und insbesondere in der Kosmologie hingegen vereinfachen sich die Formeln, wenn Lichtgeschwindigkeit und Gravitationskonstante zu 1 gesetzt werden, das ist das sogenannte geometrische Einheitensystem. Gelegentlich wird allerdings auch die Konvention 8πG = 1 benutzt.
Die Planck-Einheiten vereinigen diese Ansätze und stellen damit das natürliche Einheitensystem der Quantengravitation dar.
Definitionen
Grundgrößen
Die Planck-Einheiten ergeben sich aus einer einfachen Dimensionsbetrachtung, das heißt einer Suche nach einem mathematischen Ausdruck von der Dimension einer Länge, Zeit bzw. Masse, der nur Produkte und Quotienten von geeigneten Potenzen von G, c und
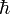 enthält, wobei
enthält, wobei  . Benutzt man zusätzlich die elektrische Permittivität 4πε0 und die Boltzmann-Konstante k, so lassen sich außerdem eine Planck-Ladung und eine Planck-Temperatur als weitere Grundgrößen bestimmen.
. Benutzt man zusätzlich die elektrische Permittivität 4πε0 und die Boltzmann-Konstante k, so lassen sich außerdem eine Planck-Ladung und eine Planck-Temperatur als weitere Grundgrößen bestimmen.Name Quantität Term Ungefähres SI-Äquivalent Andere Äquivalente Planck-Masse Masse (M) 
2,17644 · 10-8 kg [1] 1,311 · 1019 u Planck-Länge Länge (L) 
1,616252 · 10-35 m [2] 3,054 · 10-25 a0 Planck-Zeit Zeit (T) 
5,39124 · 10-44 s [3] Planck-Ladung Ladung (Q) 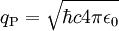
1,8755459 · 10-18 C 11,70624 e Planck-Temperatur Temperatur (Θ) 
1,416785 · 1032 K [4] Statt
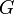 wird manchmal
wird manchmal 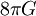 zu Eins gesetzt, dann ergibt sich als Masseeinheit die reduzierte Planck-Masse:
zu Eins gesetzt, dann ergibt sich als Masseeinheit die reduzierte Planck-Masse:Abgeleitete Größen
Neben diesen fünf Grundgrößen werden auch folgende abgeleitete Größen verwendet:
Name Quantität Term Ungefähres SI Äquivalent Planck-Energie Energie (ML2T -2) 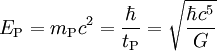
1,9561 · 109 J (= 1,2209 · 1028eV) Planck-Impuls Impuls (MLT -1) 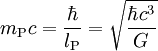
6,52485 kg m/s Planck-Kraft Kraft (MLT -2) 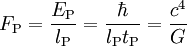
1,21027 · 1044 N Planck-Leistung Leistung (ML2T -3) 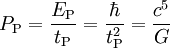
3,62831 · 1052 W Planck-Dichte Dichte (ML -3) 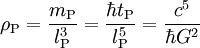
5,15500 · 1096 kg/m3 Planck-Kreisfrequenz Frequenz (T -1) 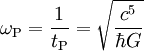
1,85487 · 1043 s-1 Planck-Druck Druck (ML-1T -2) 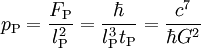
4,63309 · 10113 Pa Planck-Strom Elektrischer Strom (QT -1) 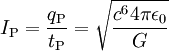
3,4789 · 1025 A Planck-Spannung Elektrische Spannung (ML2T -2Q -1) 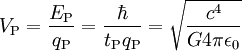
1,04295 · 1027 V Planck-Impedanz Widerstand (ML2T -1Q -2) 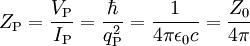
29,9792458 Ω Planck-Beschleunigung Beschleunigung (LT -2) 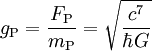
5,56 · 1051 m/s² Die Planck-Fläche
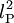 spielt insbesondere in Stringtheorien und bei Überlegungen zur Entropie Schwarzer Löcher in Zusammenhang mit dem holografischen Prinzip eine wichtige Rolle.
spielt insbesondere in Stringtheorien und bei Überlegungen zur Entropie Schwarzer Löcher in Zusammenhang mit dem holografischen Prinzip eine wichtige Rolle.Rolle als Einheitensystem
Löst man die ersten drei Gleichungen nach G, c und
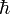 auf, so erhält man Ausdrücke, die analog nur Potenzen von lp, tp und mp enthalten, aber keine Zahlenfaktoren. Die Naturkonstanten G, c und
auf, so erhält man Ausdrücke, die analog nur Potenzen von lp, tp und mp enthalten, aber keine Zahlenfaktoren. Die Naturkonstanten G, c und 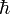 haben daher in Planck-Einheiten jeweils den Zahlenwert 1. Formuliert man Gleichungen, die diese Naturkonstanten enthalten, in Planck-Einheiten, so können sie daher entfallen, was in bestimmten Disziplinen der theoretischen Physik die Gleichungen deutlich vereinfacht, wie beispielsweise in der allgemeinen Relativitätstheorie und in den verschiedenen Ansätzen für eine Quantengravitation.
haben daher in Planck-Einheiten jeweils den Zahlenwert 1. Formuliert man Gleichungen, die diese Naturkonstanten enthalten, in Planck-Einheiten, so können sie daher entfallen, was in bestimmten Disziplinen der theoretischen Physik die Gleichungen deutlich vereinfacht, wie beispielsweise in der allgemeinen Relativitätstheorie und in den verschiedenen Ansätzen für eine Quantengravitation.Die Gravitationskonstante ist mit einem relativen Fehler von etwa 1/7000 vergleichsweise ungenau bekannt. Da sich diese Ungenauigkeit auf die Kenntnis der Planck-Einheiten überträgt, sind sie als Einheitensystem für die Experimentalphysik von untergeordneter Bedeutung. Dazu trägt auch ihre geringe Größe bei, die selbst bei den kleinsten derzeit zugänglichen Messwertbereichen zu extrem großen Zahlenwerten führen würde.
Die Planck-Einheiten ermöglichen eine alternative Sichtweise auf die fundamentalen Kräfte der Natur, deren unterschiedliche Stärke im SI-System durch die jeweiligen unterschiedlichen Kopplungskonstanten beschrieben wird. Bei Verwendung der Planck-Einheiten stellt sich die Situation wie folgt dar: Zwischen zwei Partikeln, die genau die Planckmasse und die Planckladung besitzen, wäre die Gravitationskraft und die elektromagnetische Kraft exakt gleich groß. Die unterschiedliche Stärke dieser Kräfte in unserer Welt ist die Folge davon, dass ein Proton bzw. ein Elektron eine Ladung von etwa 0,085 Planckladungen besitzt, während ihre Massen um 19 bzw. 22 Größenordnungen kleiner als die Planckmasse sind. Die Frage: "Warum ist die Gravitation so schwach?" ist also äquivalent zu der Frage: "Warum haben die Elementarteilchen so geringe Massen?".
Geschichte
Planck entdeckte die letzte zur Definition der Planck-Einheiten erforderliche Naturkonstante, das nach ihm benannte Wirkungsquantum. Er erkannte die Möglichkeit, damit ein universell gültiges System von Einheiten zu definieren und erwähnte diese bereits im Mai 1899 in seiner Publikation mit dem Titel „Über irreversible Strahlungsvorgänge“ in Sitzungsberichte der Preußischen Akademie der Wissenschaften (Band 5, S. 479, 1899). Zu dieser Zeit war die Quantenmechanik noch gar nicht entdeckt. Erst im Dezember 1900 publizierte er seine Arbeit zur Theorie der Strahlung eines Schwarzen Körpers, in der die später nach ihm benannte Konstante erstmals mit h bezeichnet wurde, und für die er 1919 den Nobelpreis für Physik für das Jahr 1918 erhielt. Das folgende Zitat vermittelt einen Eindruck von dem Stellenwert, den Planck diesen Einheiten einräumte[5]
„… ihre Bedeutung für alle Zeiten und für alle, auch außerirdische und außermenschliche Culturen nothwendig behalten und welche daher als ‚natürliche Maaßeinheiten‘ bezeichnet werden können …“
– Max Planck
Plancks System natürlicher Maßeinheiten unterscheidet sich von den heute üblichen Planck-Einheiten um einen Faktor 2π, da er nicht
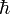 sondern das Wirkungsquantum
sondern das Wirkungsquantum 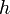 zu 1 setzte.
zu 1 setzte.Obwohl Planck diesem Einheitensystem ein Kapitel seines 1906 erschienen Buches „Theorie der Wärmestrahlung“ widmete und dies Thema auch später wieder aufgriff, konnte es sich auch innerhalb der Physik nicht etablieren. Dem Nachteil, dass seine Längen-, Zeit- und Masseeinheiten als absurd unpraktisch erachtete Werte aufwiesen, stand kein erkennbarer Vorteil gegenüber, da damals in keiner physikalischen Theorie gleichzeitig das Wirkungsquantum und die Gravitationskonstante auftauchte.
Erst nach ersten Arbeiten zur Vereinigung von Quantentheorie und Gravitation in den späten 1930ern entstand das spätere Anwendungsgebiet der Planck-Einheiten. Als John Archibald Wheeler und Oskar Klein 1955 über die Planck-Länge als Grenze der Anwendbarkeit der Allgemeinen Relativitätstheorie veröffentlichten, war Plancks Vorschlag schon fast vergessen. Nach der „Wiederentdeckung“ der Planckschen Vorschläge für ein solches Maßsystems wurde dann ab 1957 der Name Planck-Einheiten gebräuchlich.
Quellen
- ↑ http://physics.nist.gov/cgi-bin/cuu/Value?plkm
- ↑ http://physics.nist.gov/cgi-bin/cuu/Value?plkl
- ↑ http://physics.nist.gov/cgi-bin/cuu/Value?plkt
- ↑ http://physics.nist.gov/cgi-bin/cuu/Value?plktmp
- ↑ http://bibliothek.bbaw.de/bibliothek-digital/digitalequellen/schriften/anzeige/index_html?band=10-sitz/1899-1&seite:int=493
Weblinks
Siehe auch
Wikimedia Foundation.