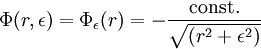Plummer-Potenzial

Das Plummer-Potential ist ein abstraktes mathematisches Potential. Es wurde nach H.C.Plummer benannt, welcher es 1911 zur Berechnung von Kugelsternhaufen einführte. Es ist weiters bei der numerischen Behandlung von Problemen nützlich, bei denen einzelne Terme gegen den Grenzwert gegen 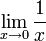$\lim_{x \to 0}\frac{1}{x}$ streben.

Durch seine nahe Verwandtschaft mit dem Coulomb- und Gravitationspotential – beides sind Spezialfälle des Plummer-Potentials – finden sich die meisten Anwendungen dieses Potentials in der Elektrodynamik und der Gravitationstheorie.

Die Potentialfunktion besitzt die Form

$\Phi(r, \epsilon) = \Phi_{\epsilon}(r) = - \frac{ \mathrm{const.} }{\sqrt{(r^2 + \epsilon^2)} }$

Setzt man nun ε = 0, so erhält man das klassische $\frac{1}{r}$ (Coulomb-)Potential, das in der Newtonschen Gravitationstheorie und in der Elektrodynamik eine wichtige Rolle spielt:

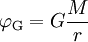$\varphi_\mathrm{G} = G \frac{M}{r}$ (Gravitations-Potential)

bzw.

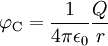$\varphi_\mathrm{C} = \frac{1}{4\pi\epsilon_0} \frac{Q}{r}$ (Coulomb-Potential)

Es bietet sich deshalb an, das Plummer-Potential und das Coulomb-Potential gegenüber zu stellen: Im Gegensatz zum Coulomb-Potential besitzt das Plummer-Potential an der Stelle r = 0 keine Singularität, sondern hat einen endlichen Wert 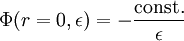$\Phi(r = 0, \epsilon) = - \frac{\mathrm{const.}}{\epsilon}$; das normale $\frac{1}{r}$-Potential hingegen ergibt für r = 0 den undefinierten Ausdruck $\frac{1}{0}$. Damit ist das Plummer-Potential im Nullpunkt stetig und differenzierbar, was für analytische Berechnungen interessant ist.

Anwendung

Eine wichtige Anwendung für das Plummer-Potential findet sich in der Astronomie, bei der Simulation der Dynamik von Sternhaufen und Galaxien. Bei Simulationen mit sehr vielen Körpern (sogenannten Mehrkörper-Simulationen) ist man oftmals nicht primär an den Kollisionen oder Beinahekollisionen einzelner Körper interessiert, sondern an den sich großräumig ausbildenden Strukturen. Da es praktisch unmöglich ist, solche Kollisionen schon bei den Anfangsbedingungen einer Simulation auszuschließen, greift man gerne auf das Plummer-Potential zurück, da es für große Abstände eine gute Approximation des Gravitationspotentials ist und für kleine Abstände nicht über alle Grenzen wächst. Kommen sich zwei Körper nun zu nahe, dann fliegen sie praktisch durcheinander durch, ohne dass eine übermäßige Kraft auftritt.