Plättbarer Graph

Planare Zeichnung des K₄

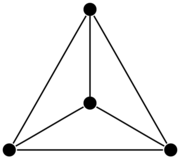
Ein planarer Graph (auch plättbarer Graph) ist in der Graphentheorie ein Graph, der auf einer Ebene mit Punkten für die Knoten und Linien für die Kanten dargestellt werden kann, so dass sich die Kanten nicht schneiden.

Der Satz von Kuratowski gibt eine weitere Charakterisierung von planaren Graphen und erlaubt die Beantwortung der Frage nach der Plättbarkeit von Graphen.

Eine konkrete Darstellung eines Graphen in der Ebene wird auch Einbettung genannt. Ein ebener Graph ist ein in die Ebene eingebetteter Graph. Durch die Einbettung wird die Ebene in zusammenhängende Gebiete geteilt, die von den Kanten des Graphen begrenzt werden. Die begrenzenden Kanten eines Gebietes bilden seinen Rand. Das Gebiet um den Graphen herum wird auch äußeres Gebiet genannt. Die Einbettung kann auch auf einer Kugeloberfläche stattfinden. Umgekehrt ist auch jeder auf einer Kugel kreuzungsfrei darstellbare Graph planar.

Zwei Einbettungen sind äquivalent, wenn es eine isomorphe Abbildung zwischen den Rändern ihrer Gebiete gibt. Es lässt sich zeigen, dass für jeden planaren Graphen auch eine Einbettung existiert, bei der die Kanten geradlinig sind.

Ein Graph heißt maximal planar oder Dreiecksgraph, wenn er planar ist und ihm keine Kante hinzugefügt werden kann, ohne dass dadurch seine Planarität verloren geht.

Ein Graph heißt fast planar oder kritisch planar, wenn der Graph durch Entfernen eines beliebigen Knotens planar wird. Bsp.: K₅ ist fast planar.

Beispiel eines kreisartig plättbaren Graphen, rechts ein ebener Graph

Ein Graph heißt kreisartig planar (oft auch außenplanar oder außerplanar), wenn er sich so in die Ebene einbetten lässt, dass alle seine Ecken auf dem Rand ein und desselben Gebiets liegen.

Die Planarität eines Graphen lässt sich mit verschiedenen Algorithmen in linearer Zeit testen. Allerdings sind diese Algorithmen nicht einfach zu implementieren.

Verbindung zu anderen Graph-Eigenschaften

In einem zusammenhängenden planaren Graphen gilt nach dem eulerschen Polyedersatz stets:

Knotenzahl + Gebietszahl - Kantenzahl = 2.

Aus dieser Eigenschaft folgt, dass planare Graphen in Bezug auf die Knotenanzahl nur linear viele Kanten haben können.

Ist ein planarer Graph 3-fach zusammenhängend, so sind alle seine Einbettungen äquivalent.

Der Vier-Farben-Satz besagt, dass sich planare Graphen mit 4 Farben färben lassen. Dreiecksfreie planare Graphen sind 3-färbbar.

Ein planarer Graph kann höchstens 5-fach zusammenhängend sein und es gibt immer einen Knoten mit Knotengrad höchstens 5

Weblinks

• Planarity - Ein Spiel, das auf planaren Graphen basiert.