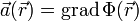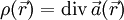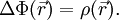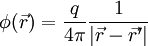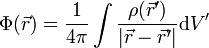Potenzialtheorie

Die Potentialtheorie behandelt die mathematisch-physikalischen Grundlagen von konservativen Kraftfeldern. Man nennt sie auch die Theorie der wirbelfreien Vektorfelder.

Wichtige Anwendungen sind das elektrische Feld, das Magnetfeld und das Gravitations- bzw. Schwerefeld. In der Fluiddynamik (Aerodynamik und Hydrodynamik) lassen sich Strömungsfelder als Potentialfeld beschreiben, ebenso viele Vorgänge in der Atomphysik und die Modellierung der Erdfigur. Die Anfänge der Theorie gehen auf C.F. Gauß und George Green zurück, wobei Gauß bereits Anwendungen für die Geoidbestimmung im Sinn hatte.

Zentrale Elemente des Theoriegebäudes sind das Potential und seine örtlichen Ableitungen, bei denen zwischen dem Innenraum eines Körpers (mit seiner Ladungs- bzw. Massenverteilung) und dem quellfreien Außenraum zu unterscheiden ist (siehe Laplace-Gleichung).

Vektor- und skalares Feld

Die Potentialtheorie beruht darauf, dass zu jedem konservativen Vektorfeld ein skalares Potentialfeld existiert, dass also in jedem Punkt das Vektorfeld 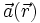$\vec a(\vec r)$ durch den Gradienten des Potentialfeldes 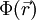$\Phi(\vec r)$ gemäß

$\vec a (\vec r) = \operatorname{grad} \, \Phi (\vec r)$

gegeben ist. Gleichzeitig lassen sich durch Bildung der Divergenz von $\vec a$ die Quellen und Senken des Feldes bestimmen (zum Beispiel die elektrischen Ladungen beim elektrischen Feld, die Massen beim Gravitationsfeld).

$\rho (\vec r) = \operatorname{div} \, \vec a (\vec r)$

Die Potentialtheorie beschäftigt sich nun damit, wie sich bei einer gegebenen Größe (z.B. Quellenfeld ρ) die anderen Größen berechnen lassen. Man spricht entsprechend der Fragestellung von Problemen.

Poisson-Problem

Für das Potential gilt die Poisson-Gleichung

$\Delta \Phi(\vec r) = \rho ( \vec r ).$

Wenn das Quellenfeld ρ gegeben ist, lässt sich das Potential durch Integration bestimmen. Da eine punktförmige Quelle am Punkt 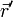$\vec r'$ mit Stärke q das Potential

$\phi ( \vec r ) = \frac{q}{4\pi} \frac{1}{|\vec r -\vec r' |}$

erzeugt, ergibt sich durch Aufsummieren insgesamt

$\Phi( \vec r ) = \frac{1}{4\pi} \int \frac{\rho (\vec r')}{|\vec r -\vec r' |} \mathrm dV'$

Dirichlet-Problem

Häufig lassen sich in der Physik die Quellenfelder nicht direkt messen, wohl hingegen ihr Potentialfeld auf einem bestimmten räumlichen Gebiet. Ein solcher Fall ist die Erforschung des Erdinneren durch geodätische oder geophysikalische Methoden:

Man kann nicht ins tiefe Erdinnere bohren, um dort die Gesteins- bzw. Massendichte zu bestimmen - man kann jedoch auf der Erdoberfläche ihre Wirkung in Form der Schwerkraft oder der Lotabweichung messen.

In einem solchen Fall ist 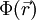$\Phi( \vec r )$ auf einem Teil des Raumes bestimmt, das Quellenfeld selbst jedoch unbekannt. Es ist nur unter gewissen Nebenbedingungen eindeutig und lässt i.a. mehrere Lösungen zu (siehe auch Umkehrproblem der Potentialtheorie).
Eine elegante mathematische Lösung des Dirichlet-Problems ist mit Hilfe der Greenschen Funktionen möglich.

Potential der einfachen Schicht

Eine Schwierigkeit bei praktischen Berechnungen in der Potentialtheorie ist oft die große zu verarbeitende Datenmenge, beispielsweise für harmonische Kugelfunktions-Entwicklungen zur Bestimmung von Schwerefeld und Geoid. Um beispielsweise aus Bahnstörungen von Satelliten 50.000 Massefunktionen des Erdkörpers zu berechnen, benötigt die Neumannsche Methode ca. 100.000 Datensätze und die Inversion von riesigen Matrizen (Gleichungssystemen).

Für dieses Problem der Satellitengeodäsie hat der Bonner Geodät Karl Rudolf Koch in den 1970er Jahren die Methode "Potential der einfachen Schicht" erarbeitet. Es ist eine sog. robuste, sehr effektive Rechenmethode, bei der das Potential nicht durch harmonische Funktionen, sondern als Flächenbelegung fiktiver dünner Schichten der Erdoberfläche dargestellt wird. Die im Prinzip an den Modellrändern unstetige Rechenmethode bewährte sich in der Praxis ungemein und konnte die Rechenzeiten der Großcomputer auf einen Bruchteil reduzieren.

Literatur

• R. J. E. Clausius Die Potentialfunction und das Potential Leipzig: Barth, 1859.
• T. Wand Die principien der mathematischen Physik und die Potentialtheorie nebst ihren vorzüglichsten Anwendungen im Grundriss dargestelt Leipzig : B. G. Teubner, 1871.
• C. Neumann Untersuchungen über das logarithmische und Newton'sche Potential Leipzig : B. G. Teubner, 1877.
• A. Wangerin Theorie des Potentials und der Kugelfunktionen (2 band) Leipzig: G. J. Göschen, 1909-1921.
• R. Courant, D. Hilbert Methoden der mathematischen Physik Zweiter Band Berlin: Springer, 1924.
• S. Axler, P. Bourdon, W. Ramey: Harmonic Function Theory. 2. Auflage, Springer-Verlag, 2001, ISBN 0387952187.
• O.D. Kellogg: Foundations of Potential Theory. Dover Publications, 1967, ISBN 0486601447.
• Karl Ledersteger: Handbuch der Vermessungskunde Band V Astronomische und Physikalische Geodäsie. J. B. Metzler, Stuttgart 1969 (Theoreme und Schwerefeld, Gleichgewichtsfiguren und Prinzip der Entblätterung, Isostasie usw.).
• Rudolf Sigl: Einführung in die Potentialtheorie. Wichmann-Verlag, 1973, ISBN 3-87907-031-8