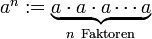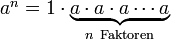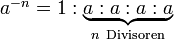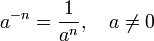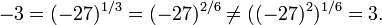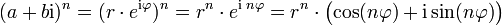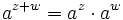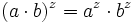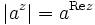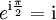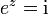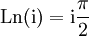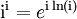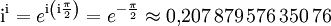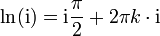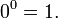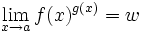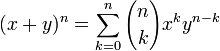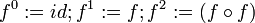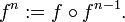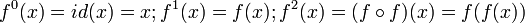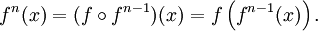- Potenzzahl
-
Das Potenzieren ist wie das Multiplizieren seinem Ursprung nach eine abkürzende Schreibweise für eine wiederholte mathematische Rechenoperation. Wie beim Multiplizieren ein Summand wiederholt addiert wird, so wird beim Potenzieren ein Faktor wiederholt multipliziert.
Inhaltsverzeichnis
Definition
Die Potenz an wird für reelle oder komplexe Zahlen a und natürliche Zahlen n definiert durch
Man spricht diese Rechenoperation als „a hoch n“, im Fall n = 2 auch „a (zum) Quadrat“ und im Fall n = 3 auch „a (zum) Kubik“.
a heißt Basis (oder Grundzahl), n heißt Exponent (oder Hochzahl) der Potenz an. Das Ergebnis ist der Wert der Potenz.
Für n = 0 wird a0 = 1 festgelegt.
Diese Definition lässt sich nicht nur auf reelle oder komplexe Zahlen, sondern auch auf beliebige multiplikative Monoide anwenden.
Abweichende Schreibweisen
Wenn hochgestelltes Schreiben nicht möglich ist (zum Beispiel in einem ASCII-Text), verwendet man oft die Schreibweise a^b (beispielsweise in Algol 60[1], in TeX-Quellcode oder in Computeralgebrasystemen wie Maple) oder gelegentlich auch a**b (beispielsweise in Fortran, Perl oder Python).
Zehnerpotenzen werden in der elektronischen Datenverarbeitung häufig mit e oder E dargestellt.
Beispiel: 1,55 E 5 := 1,55 · 105 = 155000.Verallgemeinerung
Die folgende Modifikation erleichtert die Behandlung des Sonderfalles n = 0:
Die Potenzschreibweise bedeutet „Multipliziere die Zahl 1 mit der Grundzahl so oft, wie die Hochzahl angibt“, also
Die Hochzahl 0 sagt aus, dass die Zahl 1 keinmal mit der Grundzahl multipliziert wird und alleine stehen bleibt, so dass man das Ergebnis 1 erhält.
Negative Exponenten
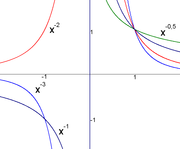
Negative Hochzahlen bedeuten, dass man die zur Multiplikation inverse Operation (Division) durchführen soll. Also „Dividiere die Zahl 1 durch die Grundzahl so oft, wie die Hochzahl angibt“.
Für eine reelle Zahl a und eine natürliche Zahl n wird definiert
Die analoge Definition wird auch in allgemeinerem Kontext angewandt, wann immer eine Multiplikation und inverse Elemente zur Verfügung stehen, beispielsweise bei invertierbaren Matrizen.
Rationale Exponenten
Ein rationaler Exponent ist als Bruch der ganzen Zahlen n und m (
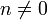 ) darstellbar. Ist a eine positive reelle Zahl, dann definiert man:
) darstellbar. Ist a eine positive reelle Zahl, dann definiert man:Dadurch kann man mit rationalen Exponenten auch das Radizieren (die Umkehrung) einer Potenz ausdrücken.
Wenn man Wurzeln aus negativen Zahlen mit ungeraden Exponenten zulässt, kann man die Definition auf negative Basen a und rationale Exponenten erweitern, wenn der Nenner des Exponenten ungerade ist. Dann gilt beispielsweise ( − 27)1 / 3 = − 3. Das Potenzgesetz (ar)s = ars gilt dann jedoch nur noch, wenn der Nenner von s ebenfalls ungerade ist, zum Beispiel ist
Für negative Basen a ist diese Funktion
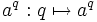 aber unstetig; beispielsweise ist ( − 1)0 = 1 aber
aber unstetig; beispielsweise ist ( − 1)0 = 1 aber 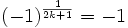 . Eine stetige Fortsetzung auf die reellen Zahlen ist also nur für positive Basen möglich.
. Eine stetige Fortsetzung auf die reellen Zahlen ist also nur für positive Basen möglich.Reelle Exponenten
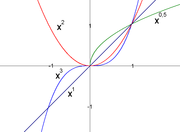
Mit analytischen Methoden kann man im Fall positiver Basis a Potenzen mit beliebigem reellem Exponenten b definieren. Für positive reelle Zahlen a und rationale Zahlen q ist die Funktion
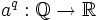 ,
, 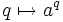
stetig und lässt sich stetig auf die reellen Zahlen fortsetzen; das Potenzieren mit beliebigen reellen Exponenten lässt sich als diese stetige Fortsetzung definieren oder äquivalent (falls die Logarithmusfunktion schon bekannt ist) als
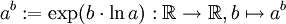 .
.
Dabei ist exp die Exponentialfunktion und ln der natürliche Logarithmus.
Rechenregeln
Das Wort „nichtnegativ“ bedeutet im folgenden „positiv oder null“; mit „alle a“ ist „alle reellen oder komplexen Zahlen a“ gemeint.
a0 = 1 für alle a (Anmerkungen zu „null hoch null“ siehe unten) 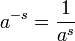
für 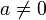 und beliebige ganze Zahlen s; oder für positive a und alle s.
und beliebige ganze Zahlen s; oder für positive a und alle s.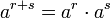
für alle a und nichtnegative ganze Zahlen r und s;
oder für alle
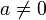 und beliebige ganze Zahlen r und s;
und beliebige ganze Zahlen r und s;
oder für positive a und alle r und s.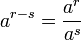
für alle 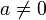 und beliebige ganze Zahlen r und s;
und beliebige ganze Zahlen r und s;
oder für positive a und alle r und s.
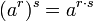
für alle a und nichtnegative ganze Zahlen r und s;
oder für alle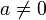 und beliebige ganze Zahlen r und s;
und beliebige ganze Zahlen r und s;
oder für positive a und beliebige reelle Zahlen r und s.Man beachte: Diese Regel ist beispielsweise für a = − 1, r = 2 und 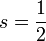 nicht anwendbar, obwohl
nicht anwendbar, obwohl
keine undefinierten Ausdrücke auftreten:
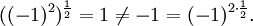
![a^{\frac{m}{n}} = \sqrt[n]{a^m}](/pictures/dewiki/52/43edac46411a2ae56ea7d55ac06fa113.png)
für alle a und nichtnegative ganze Zahlen n und ganze Zahlen m 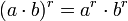
für alle a,b und nichtnegative ganze Zahlen r;
oder für alle
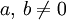 und beliebige ganze Zahlen r;
und beliebige ganze Zahlen r;
oder für positive a, b und alle r.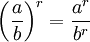
für alle 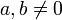 und beliebige ganze Zahlen r ; oder für positive a,b und alle r.
und beliebige ganze Zahlen r ; oder für positive a,b und alle r.Bis auf die Ausnahme
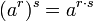 gelten die Regeln, „wann immer alle Ausdrücke definiert sind“; die genannten Bedingungen decken teilweise nicht alle Möglichkeiten ab.
gelten die Regeln, „wann immer alle Ausdrücke definiert sind“; die genannten Bedingungen decken teilweise nicht alle Möglichkeiten ab.Das Potenzieren ist weder kommutativ, denn beispielsweise gilt
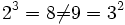 , noch assoziativ, denn beispielsweise gilt
, noch assoziativ, denn beispielsweise gilt 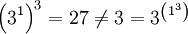 .
.Die Schreibweise
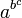 ohne Klammern bedeutet
ohne Klammern bedeutet 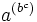 .
.Potenzen komplexer Zahlen
Ist
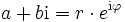 mit reellen Zahlen a, b, r > 0 und
mit reellen Zahlen a, b, r > 0 und  , dann gilt für ganze Zahlen n
, dann gilt für ganze Zahlen nInsbesondere gilt
- | zn | = | z | n für
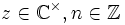 .
.
Potenzen beliebiger komplexer Zahlen mit beliebigen reellen oder sogar komplexen Exponenten lassen sich zwar durch die Formel
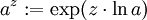 definieren. Es gibt dabei jedoch Probleme, weil der Logarithmus keine eindeutig bestimmte Fortsetzung auf ganz
definieren. Es gibt dabei jedoch Probleme, weil der Logarithmus keine eindeutig bestimmte Fortsetzung auf ganz 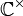 besitzt. Für positive reelle Basen a gibt es diese Probleme jedoch nicht (s. Anm. 1 unten), und es gilt beispielsweise
besitzt. Für positive reelle Basen a gibt es diese Probleme jedoch nicht (s. Anm. 1 unten), und es gilt beispielsweisefür a,b > 0 und
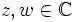 .
.Anm. 1: Für den (komplexen) Logarithmus einer positiven reellen Basis gibt es viele Werte, die sich jeweils um 2πi unterscheiden. Es kommt auf den Exponenten an: Ist er rational, so gibt es so viele Wurzeln, wie der ganzzahlige Nenner angibt. Z. B. gibt es bei einem Exponenten 1/4 vier (komplexe) Wurzeln:
11 / 4 = 1 oder i oder − 1 oder − i
Die Potenz i hoch i
Die Potenz ii der imaginären Einheit kann man mit Hilfe der eulerschen Identität wie folgt berechnen: Setzt man π / 2 in die Identität ein, erhält man
Dies bedeutet aber gerade, dass iπ / 2 eine Lösung der Gleichung
ist und damit gilt nach Definition der Logarithmusfunktion (die sich vom Reellen ins Komplexe überträgt):
(Ln mit großem L bezeichnet den Hauptwert, mehr dazu unten).
- Die Definition der Potenz zweier komplexer Zahlen z und ω lautet:
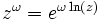
(wobei zu beachten ist, dass es sich hierbei nicht, wie im Reellen, um eine beweisbare Aussage handelt, sondern überhaupt erst eine Definition der komplexen Potenz darstellt). Möchte man nun die Potenz ii berechnen, so erhält man also:
Dies lässt sich mit dem Ergebnis von oben wie folgt schreiben:
so dass sich erstaunlicherweise ein reeller Zahlenwert ergibt.
Weitere Lösungen
Wegen der 2πi-Periodizität der komplexen Exponentialfunktion sind auch alle Werte der Form
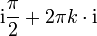 mit
mit 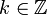
Lösungen von ez = i, damit gilt also auch
womit sich für die hier behandelte Potenz der Wert
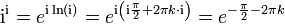 mit
mit 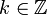
ergibt, was zeigt, dass ihr in Wirklichkeit unendlich viele Werte (die jedoch alle reell sind) zugeordnet werden, eine Eigenschaft, die die komplexe Potenz allgemein hat. Lediglich für den Hauptwert des Logarithmus, dessen Imaginärteil im Intervall
![]-\pi,\,\pi]](/pictures/dewiki/53/51a600235743d1019deb5835265ba073.png) liegt, ergibt sich der oben berechnete Wert.
liegt, ergibt sich der oben berechnete Wert.Spezielle Potenzen
Im alltäglichen Leben werden die Zehnerpotenzen, also die Potenzen mit der Basis 10 (das sind 1, 10, 100, 1000,. ..) wohl am häufigsten verwendet. Sie bilden die Grundlage unseres Zahlensystems, des Dezimalsystems.
Zur digitalen Verarbeitung von Daten am Computer wird das Dualsystem mit der Basis 2 verwendet. Die Größeneinheiten digitaler Speichersysteme sind daher die Zweierpotenzen, also die Potenzen zur Basis 2 (das sind 1, 2, 4, 8, 16,. ..). Ein Kibibyte (abgekürzt KiB) entspricht 210 = 1024 Bytes.
Für die Mathematik besonders wichtig sind die Potenzen mit der Basis
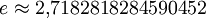 , der so genannten Eulerschen Zahl.
, der so genannten Eulerschen Zahl.Anwendungsbeispiele von Zweierpotenzen
Zweierpotenzen entsprechen dem Prozess der wiederholten Verdoppelung. Das Anwachsen dieser Zahlenfolge überrascht bei Praxisbeispielen oft.
- Ein Blatt Papier lässt sich nur etwa siebenmal auf die halbe Größe falten. Es hat dann 128 Lagen. Wenn man es (theoretisch) 42 Mal falten könnte, entspräche seine Dicke der Entfernung von der Erde zum Mond.
- Jeder Mensch hat zwei biologische Eltern, vier Großeltern, acht Urgroßeltern, usw. Verfolgt man diesen Ahnenbaum 70 Generationen zurück (ins Jahr Christi Geburt), so stammt jeder heutige Mensch von 270 = 1.180.591.620.717.411.303.424 Menschen aus dieser Zeit ab, was nicht der Gesamtzahl der Menschen entspricht, die von damals bis heute gelebt haben (60 bis 100 Milliarden). Siehe hierzu: Ahnenverlust
- Die Legende vom Erfinder des Schachspiels, der auf jedem Feld des Schachbrettes die Anzahl der Weizenkörner verdoppelte: Weizenkornlegende.
Bei Schneeballsystemen, zum Beispiel so genannten Schenkkreisen, werden zum Teil Systeme gestartet, die nicht nur eine Verdoppelung, sondern zum Beispiel eine Verachtfachung der neuen Mitglieder pro Schritt vorsehen. Solche Folgen wachsen derart schnell an, dass die Systeme bereits nach wenigen Schritten zwangsläufig kollabieren.
„Null hoch null“
In der oben gegebenen Definition wurde a0 = 1 für alle a gesetzt, also ist insbesondere
Da 0x für alle positiven x den Wert 0 hat, wäre auch der Wert 0 denkbar. Wie die Festlegung, dass 1 keine Primzahl ist, ist die Festlegung des Wertes von 00 ebenfalls keine Frage von wahr oder falsch, sondern von zweckmäßig oder unzweckmäßig. Siehe auch leeres Produkt.
„Null hoch null“ in der Mathematik
Bis Anfang des 19. Jahrhunderts haben Mathematiker anscheinend 00 = 1 gesetzt, ohne diese Festlegung genauer zu hinterfragen. Augustin Louis Cauchy listete allerdings 00 gemeinsam mit anderen Ausdrücken wie 0 / 0 in einer Tabelle von unbestimmten Ausdrücken.[2] Er wollte damit anscheinend darauf hinweisen, dass man zu jeder reellen Zahl
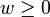 Funktionen f,g so angeben kann, dass f(a) = g(a) = 0 und
Funktionen f,g so angeben kann, dass f(a) = g(a) = 0 undGrenzwertargumente sind zur Festlegung von 00 also ungeeignet.
1833 veröffentlichte Guillaume Libri eine Arbeit[3], in der er wenig überzeugende Argumente für 00 = 1 präsentierte, die in der Folge kontrovers diskutiert wurden. Zur Verteidigung von Libri veröffentlichte August Ferdinand Möbius einen Beweis seines Lehrers Johann Friedrich Pfaff, der im Wesentlichen zeigte, dass
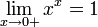 , und einen angeblichen Beweis für
, und einen angeblichen Beweis für 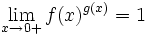 falls
falls 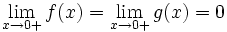 .[4] Dieser Beweis wurde durch das Gegenbeispiel f(x) = e − 1 / x und g(x) = x rasch widerlegt. In der Folge verstummte die Kontroverse und in Analysislehrbüchern verbreitete sich immer mehr die Konvention, 00 undefiniert zu lassen.
.[4] Dieser Beweis wurde durch das Gegenbeispiel f(x) = e − 1 / x und g(x) = x rasch widerlegt. In der Folge verstummte die Kontroverse und in Analysislehrbüchern verbreitete sich immer mehr die Konvention, 00 undefiniert zu lassen.Donald Ervin Knuth erwähnte 1992 im American Mathematical Monthly die Geschichte der Kontroverse und lehnte die Schlussfolgerung entschieden ab, dass 00 undefiniert gelassen wird.[5] Wenn man 00 = 1 nicht voraussetzen kann, verlangen viele mathematische Theoreme wie zum Beispiel der binomische Satz
eine Sonderbehandlung für die Fälle x = 0 oder y = 0 oder gleichzeitig n = 0 und x + y = 0.
Ebenso taucht der Ausdruck 00 in Potenzreihen wie beispielsweise für die Exponentialfunktion
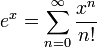 an der Stelle x = 0
an der Stelle x = 0
oder in der Summenformel für die geometrische Reihe
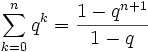 für q = 0
für q = 0
auf. Auch hier ist die Konvention 00 = 1 sinnvoll.
Die Konvention 00 = 1 ist also aus praktischen Gründen sinnvoll, weil sie die Formulierung vieler mathematischer Ausdrücke vereinfacht. 00 = 1 per Definition bedeutet aber keineswegs, dass die Funktion xy an der Stelle x = y = 0 stetig wäre.
„Null hoch null“ in der Informatik
Die Frage nach dem Wert von „null hoch null“ spielt in der Informatik insbesondere bei der Standardisierung von Programmiersprachen eine Rolle. Lange Zeit wurde das allerdings nicht beachtet, ältere Sprachnormen legen anscheinend kein bestimmtes Verhalten fest; Taschenrechner verhalten sich ebenfalls unterschiedlich und liefern üblicherweise 1, Error oder unbestimmt als Ergebnis.
William Kahan, der Hauptarchitekt des Standards IEEE 754 für binäre Gleitkommazahlen, empfahl für Zwecke der numerischen Mathematik 00 = 1 zu wählen.[6] Diese Konvention setzt sich anscheinend in der Informatik durch, so definieren der C99-Standard im Anhang F.9.4.4 sowie die Programmiersprache Java, dass pow(0.0,0.0)=1.0 ist.
Umkehrfunktionen
Da das Kommutativgesetz beim Potenzieren nicht gilt, gibt es zwei Umkehrrechenarten:
- das Wurzelziehen, um Gleichungen der Bauart xa = b zu lösen, also um die Basis zu ermitteln, wenn der Exponent bekannt ist,
- das Logarithmieren für Gleichungen des Typs ax = b, also die Bestimmung des Exponenten, wenn die Basis vorgegeben ist.
Verallgemeinerungen
Allgemeinere Basen
Allgemein gibt es Potenzen mit positiven, ganzzahligen Exponenten in jeder Halbgruppe. Hat diese ein neutrales Element und wird dadurch zum Monoid M, so ist auch Exponent 0 sinnvoll, a0 ist dann immer das neutrale Element. Es gelten die Potenzgesetze
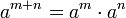
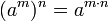
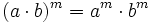 , falls a und b vertauschen, d. h. wenn ab = ba gilt.
, falls a und b vertauschen, d. h. wenn ab = ba gilt.
(Überall
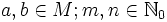 .)
.)Ist a ein invertierbares Element, so kann man mittels
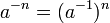 für
für 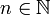
Potenzen mit beliebigen ganzzahligen Exponenten definieren. Die Rechenregeln gelten analog. Im Fall abelscher Gruppen besagen sie, dass durch die Potenzierung die Struktur eines
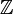 -Moduls induziert wird.
-Moduls induziert wird.Allgemeinere Exponenten
Allgemeinere Exponenten wie Matrizen werden meist nur im Zusammenhang mit der Basis e, also als Werte der verallgemeinerten Exponentialfunktion betrachtet.
Darüber hinaus wird die Potenzschreibweise gelegentlich auch für andere natürliche Fortsetzungen verwendet. So werden beispielsweise in der algebraischen Zahlentheorie gelegentlich Potenzen von Elementen von (topologischen) Galoisgruppen mit Exponenten in Vervollständigungen von
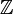 betrachtet; es handelt sich dann um die jeweils eindeutig bestimmte stetige Fortsetzung der Abbildung
betrachtet; es handelt sich dann um die jeweils eindeutig bestimmte stetige Fortsetzung der AbbildungMehrdeutigkeit der Exponentenschreibweise bei Funktionen
Eine an Potenzen erinnernde Schreibweise existiert auch für Funktionen. Diese Schreibweise kann allerdings verschiedene Bedeutungen haben. In der Regel geht aus dem Kontext hervor, welche von beiden Bedeutungen gerade gemeint ist.
Multiplikation
Als abkürzende Schreibweise für die Multiplikation mehrerer Funktionswerte trigonometrischer Funktionen mit gleichen Argumenten, wie sie beispielsweise bei den Additionstheoremen für Winkelfunktionen häufig auftreten, hat sich folgende Schreibweise eingebürgert:
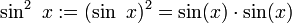 .
.
Allgemein gilt aber nicht:
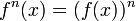 (siehe unten unter Verkettung).
(siehe unten unter Verkettung).
Verkettung
Andererseits wird die Potenzschreibweise oft als abkürzende Schreibweise für die Verkettung von Funktionen, deren Werte wieder im Definitionsbereich liegen, verwendet.
Definition (id bezeichnet die Identität auf dem Definitionsbereich):
Für die Funktionswerte bedeutet dies:
Als Erweiterung dieser Definition definiert man üblicherweise noch f − 1 als die Umkehrfunktion von f. Insbesondere findet sich diese Schreibweise auch auf vielen Taschenrechnern, beispielsweise wird dort und auch sonst die Arkusfunktion arcsin mit sin − 1 bezeichnet.
Ableitung
Wird der Exponent in Klammern geschrieben, so ist meist die entsprechende Ableitung gemeint, f(n) bezeichnet dann die n-te Ableitung von f.
Siehe auch
- Größenordnung, Wissenschaftliche Notation – zur Darstellung von Zahlen mittels Potenzen
- Potenzfolge – die Reihen und Folgen der Potenzen
Einzelnachweise
- ↑ Sample: Syntax the Algorithmic Language Algol 60
- ↑ Cauchy, Augustin-Louis. Analyse algébrique. Die Tabelle mit den unbestimmten Ausdrücken ist auf Seite 69.
- ↑ Libri, Guillaume. Mémoire sur les fonctions discontinues, Journal für die reine und angewandte Mathematik, 10 (1833), S. 303–316.
- ↑ Möbius, August Ferdinand. Beweis der Gleichung 00 = 1, nach J. F. Pfaff. Journal für die reine und angewandte Mathematik, 12 (1834), S. 134–136.
- ↑ Knuth, Donald Ervin. Two notes on notation. AMM 99 no. 5 (May 1992), 403–422. Preprint (als TeX-Quelltext) auf der Homepage von Knuth. Die Geschichte der Kontroverse ist auf Seite 6 des Preprints.
- ↑ Kahan, W. Branch Cuts for Complex Elementary Functions or Much Ado about Nothing's Sign Bit, in The State of the Art in Numerical Analysis, editors A. Iserles and M. J. D. Powell, Clarendon Press, Oxford, S. 165–212.
Siehe auch
Wikimedia Foundation.