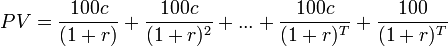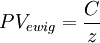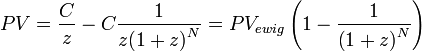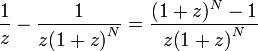- Present Value
-
Der Barwert (z. T. Gegenwartswert oder aus dem Englischen: present value) ist ein Begriff aus der Finanzmathematik . Der Barwert, ist der Wert, den zukünftige Zahlungen in der Gegenwart besitzen. Er wird durch Abzinsung der zukünftigen Zahlungen und anschließendes summieren ermittelt. Daneben gibt es noch den Begriff des versicherungsmathematischen Barwerts, welcher eine Verallgemeinerung des finanzmathematischen Barwerts darstellt.
Inhaltsverzeichnis
Barwert einer einzigen Zahlung
Im einfachsten Fall ist der Barwert einer einzige Zahlung zu ermitteln. Dazu müssen folgende Daten gegeben sein:
- die Höhe der zum zukünftigen Zahlung C,
- die Zeit T, zu der die Zahlung Z fließt, gerechnet ab heute(normalerweise in Jahren),
- der Zinssatz z, mit dem die Zahlung abgezinst wird
Der Barwert PV ist dann
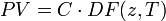 ,
,
wobei die genaue Form des Diskontierungsfaktors DF(z,T) von der gewählten Zinskonvention abhängt. Für den einfachen Fall, dass T eine ganze Zahl von Jahren bezeichnet, lautet der Barwert
 , d. h.
, d. h. 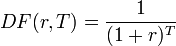
Barwert einer Anleihe
Eine häufige Anwendung der Barwertformel ist, unter Verwendung der Rendite für eine festverzinsliche Anleihe den Preis zu berechnen. Hat die Anleihe mit einem Nominalwert (Rückzahlungsbetrag) von 100 eine Laufzeit von T Jahren und zahlt jährlich einen Kupon von c (in Prozent), so berechnet sich im einfachsten Fall (ganze Anzahl T von Jahren) der Barwert aus der Summe der Barwerte der Zinszahlungen und der Rückzahlung:
Beträgt die Zeit bis zur ersten Kuponzahlung weniger als ein Jahr, enthält der Barwert zeitanteilige Stückzinsen für den ersten Kupon und wird als "dirty price" bezeichnet. Zieht man vom "dirty price" die zeitanteilig abgegrenzten Stückzinsen ab, erhält man den Marktpreis oder "clean price".
Barwert einer Annuität
Als Annuität (oder Rente) bezeichnet man in der Finanzmathematik eine gleich bleibende regelmäßige Zahlung. Wird diese Zahlung nicht auf einen Zeitraum beschränkt, sondern fließt unbegrenzt lange zu, spricht man von einer ewigen Rente (auch perpetuity).
Der Barwert des Betrages C, der einmal im Jahr auf unbeschränkte Dauer zufließt (z = Zinssatz), ist:
Für die ewige Rente gilt also der sehr einfache Zusammenhang, dass der Barwert um einen Faktor größer als die Zahlung ist, der gleich dem Kehrwert des Zinssatzes ist. Z. B. einem Zinssatz von 5% der Barwert 20 mal so groß wie die Zahlung. Man kann die ewige Rente als regelmäßigen Zins auf eine Kapitalanlage in Höhe des Barwertes betrachten.
Fließt die Rente nur N Jahre, kommt ein Korrekturfaktor hinzu:
Je größer N und je größer z, desto mehr nähert sich das Ergebnis dem einer ewigen Rente an. Begrenzt man die Laufzeit der Rente auf 30 Jahre, so beträgt bei einem Zins von 5% der Barwert der Rente das 15,4fache der jährlichen Zahlung. Der Faktor zwischen Zahlung und Barwert
heißt Rentenbarwertfaktor, sein Kehrwert heißt Annuitätenbarwertfaktor.
Versicherungsmathematischer Barwert
Der versicherungsmathematische Barwert ist eine Verallgemeinerung des finanzmathematischen Barwerts. Wo letzterer den Wert, den zukünftig anfallende Zahlungen in der Gegenwart besitzen, (nur) unter Berücksichtigung der Abzinsung darstellt, fließen beim versicherungsmathematischen Barwert auch noch statistische bzw. stochastische Größen wie (Sterbewahrscheinlichkeiten) und ähnliches ein.
Der versicherungsmathematische Barwert einer Leibrente zum Beispiel ist die Summe aller möglichen zukünftigen Rentenzahlungen (einschließlich möglicher Hinterbliebenenrentenzahlungen nach dem Tode des Rentenempfängers), jeweils mit der Wahrscheinlichkeit ihres Eintretens gewichtet und auf den Berechnungszeitpunkt abgezinst.
Siehe auch
Weblinks
Wikimedia Foundation.