Primzahlspirale

In der Mathematik ist die Ulam-Spirale oder Primzahl-Spirale eine einfache Methode, Primzahlen grafisch darzustellen. Sie wurde 1963 von dem polnischen Mathematiker Stanisław Marcin Ulam während eines wissenschaftlichen Vortrags entdeckt, als er, aus Langeweile, Zahlenreihen auf ein Papier kritzelte. Er begann mit einer „1“ in der Mitte und fuhr dann in Spiralform fort:

Dann kreiste er alle Primzahlen ein und erhielt folgendes Muster:

Ulam-Spirale der Größe 200×200

Zu seiner Überraschung befanden sich fast alle Primzahlen auf diagonalen Geraden, wie die Grafik auf der rechten Seite zeigt. Dies ist eine Ulamspirale der Größe 200×200, wobei die Primzahlen durch schwarze Punkte markiert sind. Die Diagonallinien sind deutlich sichtbar.

Es scheint, als würden die Diagonallinien immer auftauchen, unabhängig von der Größe der Spirale. Dies scheint auch dann der Fall zu sein, wenn die Anfangszahl sehr viel größer als 1 ist. Daraus folgt, dass es viele ganze Zahlen a, b und c gibt, mit denen die Funktion

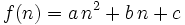$f(n) = a\,n^2 + b\,n + c\,$ mit $n \in \mathbb{Z}$

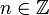
eine sehr große Menge von Primzahlen ergibt. Diese Entdeckung war so bedeutend, dass die Ulamspirale im März 1964 auf dem Titelblatt der Zeitschrift Scientific American abgebildet wurde.

Bei ausreichend großer Entfernung vom Mittelpunkt kann man auch horizontale und vertikale Linien entdecken.

Den Primzahlforschern waren diese Zahlen schon lange geläufig. Im 18. Jahrhundert hatte der Schweizer Mathematiker Leonhard Euler die Formel n² + n + 17 entdeckt, die für aufeinanderfolgende Werte n zwischen 0 und 15 jeweils Primzahlen ergab. Tatsächlich sind diese 16 Zahlen diejenigen, die auch in Ulams Schema auf der Hauptdiagonale erscheinen: 17, 19, 23, 29, 37, 47, 59, 73, 89, 107, 127, 149, 173, 199, 227 und 257. Später fand Euler eine weitere Formel, die für n zwischen 0 und 40 ausschließlich Primzahlen ergab: n² − n + 41. Durch Nachrechnen am Computer zeigte sich, dass diese zweite Eulersche Formel erstaunlich gut war, da sie für n bis 10.000.000 in 47,5 % der Fälle Primzahlen ergibt. Ulam fand weitere Formeln, deren Prozentzahlen bei der Generation von Primzahlen fast ebenso gut waren wie die der Eulerformel. Das Muster der Ulam-Spirale kann jedoch bis heute nicht vollständig erklärt werden.

Literatur

• M. Stein und S. M. Ulam: An Observation on the Distribution of Primes, Amer. Math. Monthly 74, S. 43-44 (1967)
• M. L. Stein, S. M. Ulam und M. B. Wells: A Visual Display of Some Properties of the Distribution of Primes, Amer. Math. Monthly 71, S. 516-520 (1964)
• Martin Gardner: Mathematical Recreations: The Remarkable Lore of the Prime Number, Sci. Amer. 210, S. 120-128 (März 1964)
• Paul Hoffman: Erdős, l'homme qui n'aimait que les nombres, Editions BELIN, 2000, ISBN 2-7011-2539-1

Weblinks

• Links zu anderen Seiten über die Ulam-Spirale (englisch)
• Applet, das Ulam-Spiralen zeichnet (englisch)
• Ein weiteres Applet mit Quellcode (englisch)
• http://www.abarim-publications.com/artctulam.html
• http://www.numberspiral.com/