Prüfercode

In der Graphentheorie bezeichnet ein Prüfer-Code eine Folge, die einen beschrifteten Baum eineindeutig beschreibt. Der Code für einen Baum mit n Knoten hat die Länge n−2 und kann mit einem einfachen iterativen Algorithmus erstellt werden. Prüfer-Codes wurden 1918 von Heinz Prüfer eingeführt, um den Satz von Cayley zu beweisen.

Algorithmus

Erstellt werden kann ein Prüfer-Code zu einem Baum durch das iterative Entfernen von Knoten, bis nur noch zwei Knoten übrig sind. Gegeben sei ein Baum T mit Knoten {1, 2, ..., n}. Im Schritt i wird das Blatt mit der kleinsten Beschriftung aus dem Baum entfernt und das i-te Element des Prüfer-Codes auf die Beschriftung des einzigen Nachbarn des entfernten Blattes gesetzt.

Der Code eines Baums ist offensichtlich eindeutig und hat die Länge n−2.

Beispiel

Ein beschrifteter Baum mit Prüfer-Code 5, 5, 2, 2, 2

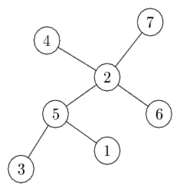
Der oben vorgestellte Algorithmus wird auf das Bild rechts angewandt. Zu Beginn ist der Knoten 1 das Blatt mit der kleinsten Beschriftung, daher wird dieser Knoten als erstes entfernt und 5 wird als erstes Element in den Prüfer-Code eingefügt. Anschließend werden die Blätter 3 und 4 aus dem Baum entfernt und die Folge um 5 und 2 erweitert. Da der Knoten 5 jetzt das kleinste Blatt ist, wird er aus dem Baum entfernt und 2 an die Folge angehängt. Als letzter Knoten wird Knoten 6 aus dem Baum entfernt und 2 an die Folge angehängt. Der Algorithmus terminiert, da nur noch 2 Knoten (2 und 7) übrig sind.

Anwendung

Der Prüfer-Code eines Baums mit n Knoten ist eine eindeutige Folge der Länge n−2 mit Elementen aus {1, ..., n}. Umgekehrt gilt, dass es zu einem gegebenen Prüfer-Code S der Länge n−2 mit Elementen aus {1, ..., n} einen eindeutigen beschrifteten Baum gibt. Das kann einfach mittels Induktion über n gezeigt werden.

Die direkte Konsequenz daraus ist, dass Prüfer-Codes eine Bijektion zwischen der Menge der beschrifteten Bäume mit n Knoten und der Menge der Folgen der Länge n−2 mit Elementen aus {1, ..., n} darstellen. Die letztgenannte Menge hat die Größe nⁿ⁻², wodurch die Existenz der Bijektion den Satz von Cayley beweist: Es gibt nⁿ⁻² beschriftete Bäume mit n Knoten.

Die Ergebnisse können verallgemeinert werden: Ein beschrifteter Baum ist ein Spannbaum eines beschrifteten vollständigen Graphen. Werden geeignete Einschränkungen an den Prüfer-Code gestellt, kann mit ähnlichen Methoden die Anzahl von Spannbäumen für vollständige bipartite Graphen ermittelt werden. Ist G ein vollständiger bipartiter Graph mit Knoten 1 bis k in einer Partition und Knoten k+1 bis n in der anderen Partition, so ist in G die Anzahl der beschrifteten Spannbäume k^n−k(n−k)^k.

Literatur

• Heinz Prüfer: Neuer Beweis eines Satzes über Permutationen. Arch. Math. Phys. 27: 742-744. 1918