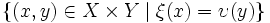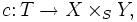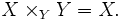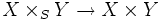- Pull-back
-
Das Faserprodukt ist ein Begriff aus dem mathematischen Teilgebiet der Kategorientheorie, der in vielen Bereichen benutzt wird. Zentrale Bedeutung kommt dem Faserprodukt in der algebraischen Geometrie zu.
Der Begriff des Faserproduktes ist dual zum Begriff des push-outs.
Inhaltsverzeichnis
Faserprodukt von Mengen
Sind ξ: X → S und υ: Y → S zwei Abbildungen von Mengen, so ist das Faserprodukt von X und Y über S die Teilmenge
des kartesischen Produktes von X und Y.
Faserprodukte in beliebigen Kategorien
Sind Morphismen ξ: X → S und υ: Y → S in einer Kategorie gegeben, so heißt ein Objekt X ×S Y zusammen mit Morphismen
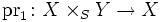 und
und 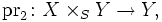
den kanonischen Projektionen, ein Faserprodukt von X und Y über S, wenn die folgende universelle Eigenschaft erfüllt ist:
- Zu jedem Paar von Morphismen (f: T → X, g: T → Y) von einem Testobjekt T nach X bzw. Y, für das
- ξf = υg (als Morphismen T → S)
- gilt, gibt es genau einen Morphismus
- so dass
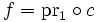 und
und 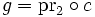
- gilt.
Anders formuliert: die Funktoren
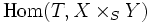 und
und 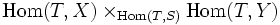
sind via pr1 und pr2 natürlich äquivalent.
Gelegentlich werden auch derartige Paare von Morphismen (f: T → X, g: T → Y) von einem Objekt T nach X bzw. Y, für die
- ξf = υg (als Morphismen T → S)
gilt, als Pullback-Kegel bezeichnet; Morphismen von Pullback-Kegeln sind über entsprechende kommutative Diagramme definiert. Das Faserprodukt ist dann das Endobjekt der Kategorie der Pullback-Kegel.
Eigenschaften
- Ist X → Y ein beliebiger Morphismus, so ist
- Sind ξ und υ injektive Mengenabbildungen (allgemein Monomorphismen), so ist das Faserprodukt der Schnitt (der Bilder) von X und Y.
- Ist S eine einpunktige Menge (allgemein ein Endobjekt), so ist das Faserprodukt gleich dem kartesischen Produkt. Allgemein gibt es einen Monomorphismus
-
- (falls beide Konstruktionen existieren).
- Für eine asymmetrische Sichtweise des Faserproduktes siehe Basiswechsel (Faserprodukt). In diesem Zusammenhang wird das Faserprodukt auch pull-back genannt.
Beispiele
- Das Faserprodukt ist ein spezieller Limes. Aus allgemeinen Gründen ist daher in den folgenden Kategorien die zugrundeliegende Menge des Faserproduktes gleich dem Faserprodukt der zugrundeliegenden Mengen:
-
- Gruppen, abelsche Gruppen, Ringe, Moduln, Vektorräume, topologische Räume, Banachräume.
- In der Kategorie der Schemata ist das Faserprodukt lokal durch Tensorprodukte gegeben. Es ist i.A. nicht das Faserprodukt der unterliegenden topologischen Räume!
- Der Gleichheitsverbund in der relationalen Algebra.
Wikimedia Foundation.