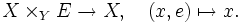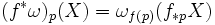Pullback

Dieser Artikel wurde auf der Qualitätssicherungsseite des Portals Mathematik eingetragen. Dies geschieht, um die Qualität der Artikel aus dem Themengebiet Mathematik auf ein akzeptables Niveau zu bringen. Dabei werden Artikel gelöscht, die nicht signifikant verbessert werden können. Bitte hilf mit, die Mängel dieses Artikels zu beseitigen, und beteilige dich bitte an der Diskussion!

In verschiedenen Teilgebieten der Mathematik bezeichnet man als Pullback (auch: Zurückziehung) Konstruktionen, die ausgehend von einer Abbildung 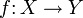$f\colon X\to Y$ und einem Objekt E, das in irgendeiner Weise zu Y gehört, ein entsprechendes, "entlang von f zurückgezogenes" Objekt für X liefern; es wird häufig mit f ^* E bezeichnet.

Das duale Konzept heißt meist Pushforward.

Der Rücktransport einer glatten Funktion

Sei 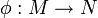$\phi : M \to N$ ein Diffeomorphismus zwischen glatten Mannigfaltigkeiten und sei 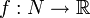$f : N \to \R$ eine glatte Funktion auf N. Dann ist der Rücktransport von f bezüglich φ eine glatte Funktion auf M, welche durch

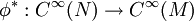$\phi^*: C^\infty(N) \to C^\infty(M)$ mit $(\phi^*(f))(x) \mapsto f(\phi(x))$

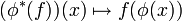
definiert ist.

Schränkt man die Funktion f auf eine offene Teilmenge 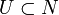$U \subset N$ ein, so erhält man ebenso eine glatte Funktion auf 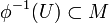$\phi^{-1}(U) \subset M$. Der Rücktransport ist also ein Morphismus zwischen den Garben der glatten Funktionen von N und M.

Faserprodukte

Hauptartikel: Faserprodukt

Ist 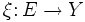$\xi\colon E\to Y$ eine Abbildung, so liefert die erste Projektion des Faserproduktes 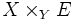$X\times_YE$ eine Abbildung mit Ziel X:

$X\times_YE\to X,\quad (x,e)\mapsto x.$

Diese Art des Pullbacks wird auch als Basiswechsel bezeichnet. Die Zurückziehung von Vektorbündeln ist ein wichtiger Spezialfall.

Man beachte, dass die kategoriell duale Konstruktion nicht Pushforward, sondern Pushout heißt.

Pullback von Differentialformen

Hauptartikel: Differentialform

Sind M und N differenzierbare Mannigfaltigkeiten und 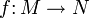$f\colon M\to N$ eine differenzierbare Abbildung, und ist ω eine k-Form auf N, so gibt es eine zurückgezogene Differentialform f ^* ω auf M, die im Fall von 1-Formen durch

$(f^*\omega)_p(X)=\omega_{f(p)}(f_{*p}X)\,$

für Tangentialvektoren 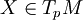$X\in T_pM$ im Punkt 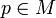$p\in M$ definiert ist.

Literatur

• Otto Forster: Riemannsche Flächen, Springer 1977, englisch Lectures on Riemann surfaces, Graduate Texts in Mathematics, Springer-Verlag, 1991, ISBN 3540906177
• R. Abraham, Jerrold E. Marsden, & T. Ratiu: Manifolds, Tensor Analysis and Applications., Springer-Verlag, Berlin 2003, ISBN 0-201-10168-8