Pythagoräischer Körper

In der Mathematik bezeichnet ein Körper eine Menge von Elementen (etwa Zahlen), auf der die vier Grundrechenarten gemäß gewisser Regeln anwendbar sind. Diese Menge wird als pythagoreisch bezeichnet, wenn zusätzlich der Satz des Pythagoras dort immer gilt.

Dies ist nämlich nicht selbstverständlich: Ein aus der Schulmathematik bekannter Körper ist derjenige der Brüche. Jede beliebige Summe oder Differenz, jedes Produkt und jeder Quotient ist darin immer ermittelbar. Trotzdem gilt darin nicht der Satz des Pythagoras, denn 1² + 1² = 1 + 1 = 2 ist kein Quadrat eines Bruches.

In der mathematischen Theorie der pythagoreischen Körper wird verschiedenen Fragestellungen nachgegangen: Zum Beispiel wird untersucht, was notwendig ist, einen Körper pythagoreisch zu machen (dies führt zum pythagoreischen Abschluss).

Pythagoreische Körper spielen auch eine Rolle bei der Betrachtung der euklidischen Körper.

Definition

Ein Körper K heißt pythagoreisch, wenn die Summe von zwei Quadraten in K bereits wieder ein Quadrat ist. Ein Körper K heißt strikt-pythagoreisch, wenn alle seine formalreelle quadratische Erweiterungen pythagoreisch sind.^[1]

Gerne verwendet wird folgendes Lemma:
Ein Körper K ist genau dann pythagoreisch, wenn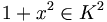 $1+x^2\in K^2$ für jedes $x\in K$.

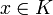Siehe auch

• Pythagoraszahl

Quellen

1. ↑ Bröcker L., Über eine Klasse pythagoreischer Körper, Archiv der Mathematik, Volume 23, Number 1, Dezember 1972, S. 405-407