- Quadrantentabelle
-
Dieser Artikel befasst sich mit dem geometrischen Quadranten. - Für das astronomische Gerät zur Positionsbestimmung von Gestirnen siehe: Quadrant (Astronomie).
- Für die Quadranten-Bezeichnungen in der Zahnmedizin siehe: Zahnschema.
- Für den Schweizer Hersteller von thermoplastischen Werkstoffen siehe: Quadrant AG.
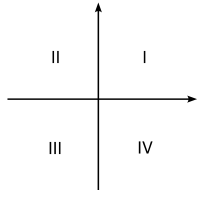
Der Quadrant (latein quadrans „Viertel“) ist ein durch zwei Koordinatenachsen begrenzter Abschnitt einer Ebene, wobei die Punkte auf den begrenzenden Achsen in der Regel zu keinem Quadranten gehören.
Nach den üblichen Konventionen wird der erste Quadrant rechts oben gezeichnet. In einem Kartesischen Koordinatensystem werden sie entgegen dem Uhrzeigersinn mit I, II, III, IV bzw. 1, 2, 3, 4 bezeichnet. Ein Punkt im ersten Quadranten hat dann jeweils positive Koordinaten.
Es sind jedoch auch andere Einteilungen gebräuchlich.
| Quadrant | I | II | III | IV |
|---|---|---|---|---|
| x-Koordinate | > 0 | < 0 | < 0 | > 0 |
| y-Koordinate | > 0 | > 0 | < 0 | < 0 |
Bezug zur Trigonometrie
In der Trigonometrie hängen Vorzeichen der Winkelfunktionen Sinus, Cosinus, Tangens bzw. Cotangens – und deren 360°-Perioden – davon ab, bis in welchen Quadranten der Winkel sich erstreckt:
| α | sinα | cosα | tanα | cotα | |
|---|---|---|---|---|---|
| 1. Quadrant | 0–90° | + | + | + | + |
| 2. Quadrant | 90–180° | + | − | − | − |
| 3. Quadrant | 180–270° | − | − | + | + |
| 4. Quadrant | 270–360° | − | + | − | − |
Jede der trigonometrischen Winkelfunktionen hat in zwei Quadranten dasselbe Vorzeichen. Daher ist das Urbild des Wertes einer trigonometrischen Funktion, z.B. des Sinus mehrdeutig. Etwa sinα < 0 kann aus einem Winkel α im 3. oder 4. Quadranten, also π < α < 2 · π bzw. 180° < α < 360° resultieren.
Eine Quadrantentabelle – bzw. eine entsprechende Abfrage in einem PC-Programm – ist in der Geodäsie oder Navigation immer notwendig, um aus Koordinaten zweier Punkte die Richtung (das Azimut, den Kurs) zu berechnen.
Siehe auch
Wikimedia Foundation.