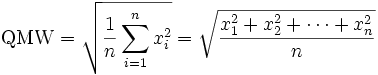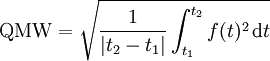Quadratmittel

Das quadratische Mittel ist eine Methode zur Mittelwert-Bildung einer Zahlen- oder Messreihe (siehe auch: Potenzmittelwert). Bei der quadratischen Mittelung haben – im Gegensatz zum geometrischen Mittel – größere Werte einen stärkeren Einfluss als kleinere. Der quadratische Mittelwert (häufige Abkürzung QMW) wird im Englischen Root Mean Square (oder RMS) bezeichnet.

Berechnung

Für die Berechnung des QMW einer Zahlenreihe werden zunächst die Quadrate aller Zahlenwerte addiert und durch ihre Anzahl n dividiert. Die Quadratwurzel daraus ergibt den QMW.

$\mathrm{QMW} = \sqrt{\frac{1}{n}\sum_{i=1}^n{x_i^2}} = \sqrt {{x_1^2 + x_2^2 + \cdots + x_n^2} \over n}$

Aus geometrischer Sicht ermittelt man aus der Zahlenreihe Quadrate und ermittelt damit ein Quadrat durchschnittlicher Fläche bzw. ein Quadrat mittlerer Größe, es handelt sich also um einen Mittelwert über eine Fläche.

Für kontinuierliche Signale, beispielsweise dem sinusförmigen Wechselstrom, muss über den betrachteten Bereich bzw. einer Periode integriert werden:

$\mathrm{QMW} = \sqrt{ \frac{1}{|t_2-t_1|} \int_{t_1}^{t_2} {f(t)^2 \, \mathrm{d}t} }$

Wegen der Quadrierung wird er auch „zweites (absolutes) Moment“ genannt, das „dritte Moment“ wäre die Mittelung in der 3. Potenz usw.

Das folgende kleine Beispiel zeigt einen Vergleich zwischen arithmetischem Mittel („Durchschnitt“), quadratischem und geometrischem Mittel:

gegebene Zahlenreihe  (nach Größe geordnet):     10, 12, 14, 20

Arithmetisches Mittel:   $\frac{10+12+14+20}{4} = \frac{56}{4} = 14{,}00$

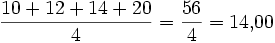Geometrisches Mittel:    $\sqrt[4]{10\cdot 12\cdot 14\cdot 20} = \sqrt[4]{33600} \approx 13{,}54$

Quadrat. Mittelwert:     $\sqrt{\frac{10^2+12^2+14^2+20^2}{4}} = \sqrt{\frac{840}{4}} \approx 14{,}49$

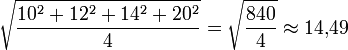
Man sieht, dass der stärker abweichende Wert „20“ geometrisch weniger, quadratisch aber eine größere Rolle spielt als beim einfachen (arithmetischen) Mitteln. Unter normalen Umständen würde man ihn vielleicht als „Ausreißer“ ansehen und weglassen. Ist er hingegen der Spitzenwert z. B. einer variablen elektrischen Spannung, verdient er tatsächlich eine stärkere Berücksichtigung als die kleineren Werte (siehe auch Fassregel).

Anwendung

In der Technik hat das quadratische Mittel große Bedeutung bei periodisch veränderlichen Signalen wie dem Wechselstrom, dessen Stromwärme (Leistungsumsatz in einem Ohmschen Widerstand) mit dessen Quadrat ansteigt. Man spricht hier vom Effektivwert des Stromes. Der gleiche Zusammenhang gilt bei zeitlich veränderlichen Spannungen.

Bei einem periodischen Signal von Sinus-ähnlicher Form beträgt der QMW das 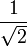$\frac{1} {\sqrt{2}}$ -fache des Scheitelwerts, also ca. 70,7 %. Weiß man hingegen nichts über die Natur der gemessenen Schwankungen, sind meist die beiden anderen Methoden der Mittelung verlässlicher. Bei einer völlig zufallsbedingten Schwankung der Werte ist hingegen der Durchschnitt (arithmetisches Mittel) der wahrscheinlichste Wert.

Siehe auch

• mittlere quadratische Abweichung, Median
• Messtechnik, Streuung, Varianz
• Methode der kleinsten Quadrate, Ausgleichungsrechnung
• Regelgüte

Weblinks

• Mittelwertsatz der Integralrechnung