Quantenhalleffekt

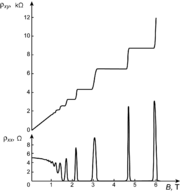
Der Quanten-Hall-Effekt (kurz: QHE) äußert sich darin, dass bei tiefen Temperaturen und starken Magnetfeldern die senkrecht zu einem Strom erzeugte Hall-Spannung nicht linear mit dem Magnetfeld anwächst wie beim klassischen Hall-Effekt, sondern dass sie Stufen aufweist.

Der Hall-Widerstand, also das Verhältnis der Hall-Spannung zum Strom, nimmt dabei als Plateauwerte ganzzahlige Teile der Größe R_K = h/e² an, wobei h das Planck'sche Wirkungsquantum und e die Elektronenladung sind. Beides sind Naturkonstanten; die Plateauwerte hängen also weder von den Materialeigenschaften wie der Ladungsträgerdichte, noch von der Probengröße, noch von der Magnetfeldstärke ab. Für diese Erkenntnis erhielt Klaus von Klitzing im Jahr 1985 den Physik-Nobelpreis.^[1]

Die als Klitzing-Konstante bezeichnete Größe R_K wird inzwischen zur Norm-Definition des elektrischen Widerstandes verwendet.

Man unterscheidet den Integralen Quanten-Hall-Effekt mit nur ganzzahligen Nennern von R_K vom Fraktionalen Quanten-Hall-Effekt, bei dem der Hallwiderstand im Verhältnis von Brüchen zu R_K steht (siehe unten).

Beschreibung des Phänomens

Hall-Widerstand und elektrischer Widerstand in Abhängigkeit vom Magnetfeld

Beim klassischen Hall-Effekt fließt elektrischer Strom durch eine Platte, die senkrecht zu ihrer Oberfläche von einem Magnetfeld durchsetzt wird. Die im Magnetfeld fließenden Ladungsträger werden durch die Lorentzkraft seitlich abgelenkt, so dass an den Kanten der Platte quer zur Stromrichtung eine elektrische Spannung gemessen werden kann, die als Hall-Spannung bezeichnet wird.

Das Verhältnis der seitlich anliegenden Hall-Spannung zum Strom wird als Hall-Widerstand bezeichnet und ist beim klassischen Hall-Effekt 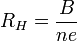$R_H =\frac {B}{n e}$, wobei B die Magnetfeldstärke, n die Ladungsträgerdichte und e die Elektronenladung sind. Der klassische Hall-Widerstand ist also insbesondere proportional zum anliegenden Magnetfeld. Man sieht dies im Bild für kleine B-Feld-Werte.

Bei hinreichend tiefer Temperatur und starkem Magnetfeld nimmt der Hall-Widerstand jedoch unabhängig vom Material einen der Plateau-Werte 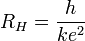$R_H =\frac{h}{k e^2}$ an, wobei k=1,2,… ganze Zahlen, h = das Plancksche Wirkungsquantum und e = die Elementarladung sind. Eine Veränderung der Magnetfeldstärke lässt den Hall-Widerstand konstant, bis dieser auf einen anderen Stufenwert wechselt. In der Mitte der Stufen verschwindet die in Stromrichtung an der Probe anliegende Spannung U_x, das heißt der elektrische Widerstand verschwindet dort und die Leitung wird disspiationsfrei. Bei den Plateauzuständen des Quanten-Hall-Effekts handelt es sich also ähnlich der Supraleitung um einen makroskopischen Quantenzustand.

Versuchsbedingungen

Versuche zur Beobachtung des Quanten-Hall-Effektes werden in einem Kryostaten bei 4,2 K durchgeführt, also bei der Temperatur von flüssigem Helium. Man benötigt Magnetfelder von 5 bis 20 Tesla, was ungefähr dem Millionenfachen der Erdmagnetfeldstärke entspricht. Als Magnetfeldquelle wird dabei ein Paar von supraleitenden Spulen eingesetzt. Der Strom durch die Probe liegt in der Größenordnung von 10 μA.

Die beim QHE verwendeten Proben sind MOSFETs (metal oxide semiconductor field effect transistors), bei denen die Ladungsträgerdichte durch eine am Transistorgatter angelegte Spannung verändert werden kann, oder aber Halbleiter-Isolator-Heterostrukturen (z. B. Ga_xAl_1-xAs/GaAs-Heterostrukturen), also dünne Plättchen, die einen Übergang zwischen einem Isolator und einem Halbleiter besitzen. An einer solchen Grenzschicht verlieren die Elektronen eine Bewegungsrichtung: die z-Richtung, in der das Magnetfeld angelegt wird, ist im Grenzpotential durch eine Quantenzahl fixiert, die Besetzungswahrscheinlichkeit des nächsthöheren Energieniveaus ist verschwindend gering. Man spricht daher von einem zweidimensionalen Elektronengas.

Die niedrige Temperatur ist notwendig, damit die mittlere freie Weglänge der Elektronen größer wird als die Radien der Kreisbahnen, auf denen sich die Elektronen im Magnetfeld bewegen würden.

Theorie

Leitfähigkeitstensor

Aufgrund eines Magnetfelds oder von bevorzugten Leitungsrichtungen in einem Festkörper ist das Ohm'sche Gesetz allgemein mithilfe eines Leitfähigkeitstensors σ zu schreiben:

$\vec j = \sigma \vec E$.

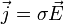In zwei Dimensionen sind dabei Leitfähigkeit σ und der Widerstand ρ 2x2-Matrizen:

$\sigma = \left(\begin{array}{cc} \sigma_{xx} & -\sigma_{xy} \\ \sigma_{xy} & \sigma_{xx} \end{array} \right),\ \ \rho = \sigma^{-1} = \frac{1}{\sigma_{xx}^2 + \sigma_{xy}^2} \left(\begin{array}{cc} \sigma_{xx} & \sigma_{xy} \\ -\sigma_{xy} & \sigma_{xx} \end{array} \right)= \left(\begin{array}{cc} \rho_{xx} & \rho_{xy} \\ -\rho_{xy} & \rho_{xx} \end{array} \right)$.

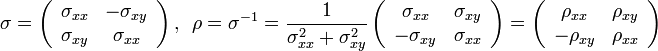Wählt man für die Beschreibung des QHE x als die Stromrichtung, y als die seitliche Richtung, in die die Hall-Spannung anliegt, und z als die Magnetfeldrichtung, so gilt aufgrund der Anordnung j_y = 0.

Gekreuztes E- und B-Feld

Die klassische Bewegung von freien Elektronen, die sich in zueinander senkrecht stehendem elektrischem und magnetischem Feld befinden, ist eine auf Spiralbahnen entlang des B-Feldes und kann als Überlagerung der folgenden Komponenten aufgefasst werden:^[2]

• eine Kreisbewegung mit der Zyklotronfrequenz 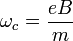$\omega_c = \frac{eB}{m}$ um die B-Feld-Richtung,
• einer Drift-Bewegung mit v_D = − E / B senkrecht zu E- und B-Feld,
• einer unbeschleunigten Bewegung in B-Feld-Richtung.

Die Zyklotronfrequenz spielt auch beim QHE eine wichtige Rolle, wie wir gleich sehen werden.

Quantenmechanische Betrachtung

Mit 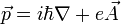$\vec p = i\hbar \nabla + e \vec A$, der Eichung 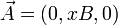$\vec A = (0, xB, 0)$ und dem Separationsansatz 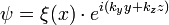$\psi = \xi(x)\cdot e^{i(k_y y+ k_z z)}$ kann die Schrödingergleichung für das freie Elektron, also

$\frac{\vec p^2}{2m}\ \psi\ =\ E\ \psi$,

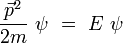in eine Differentialgleichung für die x-abhängige Funktion ξ umgeformt werden, die die Schrödingergleichung eines harmonischen Oszillators um den Ruhepunkt 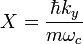$X=\frac{\hbar k_y}{m \omega_c}$ ist. Man erhält als Energieeigenwerte die Landau-Niveaus

$E = E_z + (\nu + \frac{1}{2})\ \hbar \omega_c$.

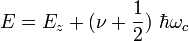Bei einer Probenabmessung von L_x in Stromrichtung und von L_y in Richtung der Hall-Spannung gilt dann: Die Wellenzahl in y-Richtung kann die Werte 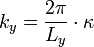$k_y = \frac{2\pi}{L_y}\cdot \kappa$ mit ganzzahligem κ annehmen, sie taucht aber auch in der Ruhelage des harmonischen Oszillators auf, für die 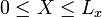$0\leq X \leq L_x$ gilt. Daraus ergibt sich für κ der Wertebereich

$0\leq \kappa \leq L_x L_y \frac{e B}{h}$.

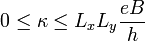Jeder Landau-Zustand hat also in diesem Bauteil den Entartungsgrad $N_L = \frac{e B}{h}$.

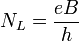Vereinfachte Erklärung des QHE

Die Position der Landau-Niveaus zueinander ändert sich über 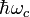$\hbar \omega_c$ mit dem B-Feld. Die Fermi-Kante, also der Energiewert, bis zu dem sich freie Elektronen im Festkörper befinden, liege zwischen den Niveaus k und k + 1. Wie oben festgestellt wurde verschwindet die Komponente U_x in der Mitte der Plateaus. Aus der Anzahl von Ladungsträgern, der jeweiligen Ladung und ihrer Driftgeschwindigkeit lässt sich die Stromdichte bestimmen:

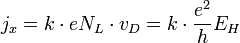$j_x = k \cdot e N_L \cdot v_D = k \cdot \frac{e^2}{h} E_H\ \$, woraus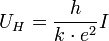 $\ \ U_H = \frac{h}{k\cdot e^2} I$

folgt. Wird B verändert, so bleibt diese Spannung konstant, bis ein neues Landau-Niveau an die Fermikante stößt und k seinen Wert ändert.

Zusammenhang mit Magnetflussquanten

Wird der Entartungsgrad mit der Probenfläche multipliziert, so erhält man den folgenden Zusammenhang:

Elektronen pro Landau-Niveau = 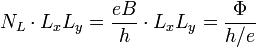$N_L \cdot L_x L_y = \frac{e B}{h} \cdot L_x L_y = \frac{\Phi}{h/e}$ = Flussquanten in der Probe.

Im Plateauzustand rotiert um jeden Magnetflussquant also die gleiche Anzahl k von Elektronen.^[3]

Dieser Zusammenhang spielt insbesondere beim Fraktionalen Quanten-Hall-Effekt eine Rolle, bei dem sich aus Elektronen und Flussquanten Quasiteilchen bilden.

Notwendigkeit der Versuchsbedingungen

Das starke Magnetfeld ist einerseits dazu notwendig, dass die Landau-Niveaus voneinander getrennt sind. Es bringt aber auch die Anzahl von Flussquanten in dieselbe Größenordnung wie die Anzahl von freien Ladungsträgern.

Die Übergänge auf höhere Landau-Niveaus sind thermisch nur bei niedrigen Temperaturen unwahrscheinlich. Ebenso wird die Einschränkung auf zwei Dimensionen benötigt, um E_z als einen festen Wert ansehen zu können.

Geschichte

Der QHE geht kontinuierlich aus dem klassischen Hall-Effekt hervor, wenn die Temperatur abgesenkt, Proben mit höherer Ladungsträgerbeweglichkeit untersucht werden und das Magnetfeld stark anwächst. Abhängig von diesen Parametern tritt der Quanten-Hall-Effekt bei sehr hohen Magnetfeldern auf. Die späte Entdeckung des Effekts beruht unter anderem darauf, dass − im Gegensatz zu vielen anderen physikalischen Größen − die apparative Erzeugung von dauerhaften Magnetfeldern verhältnismäßig stark limitiert ist (20−40 Tesla). Deshalb dauerte der Übergang vom klassischen Hall-Effekt, der seit 1879 bekannt ist, zum Quanten-Hall-Effekt mehr als 100 Jahre, bis genügend hochbewegliche Elektronensysteme in Halbleiter-Heterostrukturen zur Verfügung standen.

Obwohl die Plateaus im Hall-Widerstand bereits früher beobachtet wurde, wurden die Werte erst 1980 am Hochfeldmagnetlabor in Grenoble (GHMFL) (damals noch dt.-frz. Kooperation von MPI-FKF und CNRS) durch Klaus von Klitzing mit Naturkonstanten in Verbindung gebracht.

Da die von-Klitzing-Konstante R_K eine universelle Bezugsgröße für die Messung von Widerständen ist, die überall auf der Welt exakt reproduziert werden kann, wird seit 1990 durch internationale Übereinkunft die elektrische Maßeinheit Ohm durch diese Konstante festgelegt. Sie hängt über zwei weitere Konstanten mit der Feinstrukturkonstanten α aus der Quantenelektrodynamik zusammen (R_Kα = μ₀c / 2 mit der magnetischen Feldkonstante μ₀ und der Lichtgeschwindigkeit c).^[4]

Varianten und verwandte Effekte

Gebrochenzahliger Quanten-Hall-Effekt (Fraktionaler QHE)

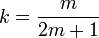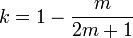Wenige Jahre nach der Entdeckung des Quanten-Hall-Effekts wurden in GaAs zusätzliche Plateaus mit nicht-ganzzahligem k gefunden (siehe Horst Ludwig Störmer), wobei viele konkrete Ähnlichkeiten zum ganzzahligen Quanten-Hall-Effekt auftreten. Gut beobachtbar sind gebrochene Quantenzahlen k, für die $k = \frac{m}{2m+1}$ oder $k = 1 - \frac{m}{2m+1}$ gilt.^[5]

Ursache für die Ähnlichkeiten ist anscheinend die Tendenz der Elektronen, zusammen mit dem Magnetfeld gebundene Zustände (composite fermions) zu bilden. Die gebundenen Zustände bestehen hier jeweils aus einem Elektron und einer geraden Anzahl magnetischer Flussquanten.

Ungewöhnlicher Quanten-Hall-Effekt in Graphen-Monolagen

In dem im Jahr 2004 erstmals hergestellten Material Graphen wurde der Quanten-Hall-Effekt bei Raumtemperatur beobachtet.^[6]

Wegen der Besonderheiten in der Dispersion ist in diesem Material (siehe Graphen) die Treppenstruktur der ganzzahligen Quanten-Hall-Plateaus, 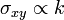$\sigma_{xy}\propto k$, für alle Stufen genau „um 1/2 verschoben“, 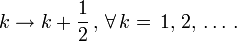$k\to k+\frac{1}{2}\,,\,\forall \,k=\, 1,\, 2,\,\dots\, .$^[7] Die „Zwei-Valley“-Struktur von Graphen und die Spin-Entartung ergeben einen zusätzlichen Faktor 4. Die Differenz der Plateauzentren ist aber immer noch ganzzahlig.

Quanten-Spin-Hall-Effekt

Forscher der Princeton University berichteten in der Zeitschrift Nature vom 24. April 2008 über Quanten-Hall-artige Effekte in Kristallen aus Wismut-Antimon, ohne dass ein externes Magnetfeld angelegt werden musste. Diese Bismut-Antimon-Legierung ist ein Beispiel eines topologischen Metalls. Die Spinströme konnten jedoch nur indirekt gemessen werden.^[8][9]

Die direkte Messung von Spinströmen in solchen Bi-Sb-Legierungen gelang 2009 einem internationalen Team, darunter Dr. Gustav Bihlmayer vom Forschungszentrum Jülich. Die Spinströme fließen ohne äußeren Anreiz aufgrund der inneren Struktur des Materials. Der Informationsfluss erfolgt verlustfrei, selbst bei leichten Verunreinigungen.^[10]

Einzelnachweise

1. ↑ K.v. Klitzing: The QHE (Nobelvortrag 9.12.1985), Rev. Mod. Phys. 58 (1986) 519.
2. ↑ K. Kopitzki: Einführung in die Festkörperphysik, B.G. Teubner, ISBN 3-519-13083-1.
3. ↑ J. Hajdu, B.Kramer: Der QHE, Phys. Blätter. 41 Nr.12 (1985) 401.
4. ↑ K.v. Klitzing: The Fine-Structure Constant α, A Contribution of Semiconductor Physics to the Determination of α, Festkörperphysik, XXI (1981) 1.
5. ↑ H.L.Strömer, M.Hill: Der fraktionale QHE, Phys. Blätter, Nr. 9 (1984).
6. ↑ K. S. Novoselov, Z. Jiang, Y. Zhang, S. V. Morozov, H. L. Stormer, U. Zeitler, J. C. Maan, G. S. Boebinger, P. Kim, A. K. Geim: Room-Temperature Quantum Hall Effect in Graphene. In: Science. 315, Nr. 5817, 2007, S. 1379 (doi:10.1126/science.1137201) (http://www.sciencemag.org/cgi/content/abstract/315/5817/1379). 
7. ↑ Geim, A.K., Novoselov, K.S., The rise of graphene, Nature Materials 6 (2007) 183-191
8. ↑ D. Hsieh, D. Qian, L. Wray, Y. Xia, Y.S. Hor, R.J. Cava, und M.Z. Hasan, A topological Dirac insulator in a quantum spin Hall phase, Nature, 452, 970-974 (2008). doi:10.1038/nature06843
9. ↑ Andreas Stiller, ct: Forscher entdecken Quanten-Hall-Effekt ohne externes Magnetfeld. Abgerufen am 23. April 2009.
10. ↑ D. Hsieh, Y. Xia, L. Wray, A. Pal, J.H. Dil, F. Meier, J. Osterwalder, G. Bihlmayer, C.L. Kane, Y.S. Hor, R.J. Cava, M.Z. Hasan: Observation of unconventional quantum spin textures in topologically ordered materials. Science, 13 February 2009, Vol 323, Issue 5916. doi:10.1126/science.1167733 Pressemitteilung FZ Jülich

Literatur

• Zyun F. Ezawa: Quantum Hall Effects. Field Theoretical Approach and Related Topics. World Scientific, Singapore 2008, ISBN 978-981-270-032-2. 
• Benoît Douçot et al. (Hrsg.): The Quantum Hall Effect. Poincaré Seminar 2004. Birkhäuser, Basel 2005, ISBN 978-3-7643-7300-9. 
• Sankar D. Sarma, Aron Pinczuk (Hrsg.): Perspectives in Quantum Hall Effects. Novel Quantum Liquids in Low-Dimensional Semiconductor Structures. Wiley-VCH, Weinheim 2004, ISBN 978-0-471-11216-7. 
• Lucjan Jacak, Piotr Sitko, Konrad Wieczorek und Arkadiusz Wojs: Quantum Hall Systems. In: The International Series of Monographs on Physics. Braid Groups, Composite Fermions, and Fractional Charge. Nr. 119, Oxford University Press, Oxford 2003, ISBN 0-19-852870-1. 

Weblinks

• Physikalisch-Technische Bundesanstalt
• Der Quanten-Hall-Effekt
• TU-Berlin – Neues vom Quanten-Hall-Effekt