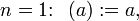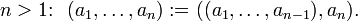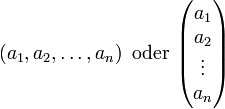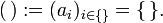Quintupel

Ein geordnetes Tupel, auch einfach nur Tupel genannt, ist eine Erweiterung des Begriffes des mengentheoretisch definierten geordneten Paares (z. B. nach der Definition von Kuratowski). Man definiert ein Tupel der Länge n oder kurz ein n-Tupel als eine Aufzählung von n nicht notwendig von einander verschiedenen mathematischen Objekten in einer vorgegebenen, festen Reihenfolge. Diese können von 1 bis n durchnummeriert werden und man spricht dann von der ersten Komponente des Tupels, von der zweiten Komponente usw. Ein 1-Tupel heißt auch Single (Einzel), ein 2-Tupel, also ein geordnetes Paar, Double (Doppel), ein 3-Tupel Tripel, ein 4-Tupel Quadrupel usw. Zwei Tupel sind genau dann gleich, wenn sie gleichlang sind und ihre jeweiligen Komponenten gleich sind.

Davon zu unterscheiden sind ungeordnete n-Tupel, die nur einfache, endliche Mengen sind und durch die Vereinigung von n einelementigen Mengen gebildet werden.^[1] So gilt z. B. für ungeordnete 2-Tupel {a,a} = {a} sowie {a,b} = {b,a}, falls 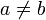$a \neq b$, während dies für die entsprechenden (geordneten) 2-Tupel nicht gilt.

Definition

(Geordnete) n-Tupel, 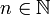$n \in \mathbb N$, werden üblicher Weise definiert als erweiterte geordnete Paare:^[2]

$n=1\colon\;\; (a):= a,$

$n>1\colon\;\; (a_1,\ldots,a_n) := ((a_1,\ldots,a_{n-1}),a_n).$

Notation

Die Niederschrift eines Tupels erfolgt üblicher Weise durch Hintereinander- oder Untereinanderschreiben von Termen für die einzelnen Glieder in der vorgegebenen Reihenfolge. Zwischen die Terme werden meist Trennzeichen, zum Beispiel das Komma, gesetzt, auch wird ohne Trennzeichen geschrieben. Zusätzlich kann eine Niederschrift in Klammern eingeschlossen werden, welche Klammerart dabei verwendet wird, hängt vom jeweiligen mathematischen Kontext ab. Zum Beispiel ist (1,4,1,3) ein 4-Tupel und allgemein bezeichnet

$(a_1,a_2,\ldots,a_n)\,\text{ oder }\begin{pmatrix}a_1\\ a_2\\ \vdots\\ a_n\end{pmatrix}$

ein n-Tupel.

Beispiele

1-Tupel: $\;\; a$.

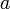3-Tupel: 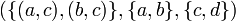$\;\; (\{(a,c),(b,c)\}, \{a,b\}, \{c,d\})$ dieses Tripel ist die Funktion

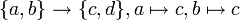$\{a,b\} \rightarrow \{c,d\}, a \mapsto c, b \mapsto c$ (nach der Definition mit Graph, Definitions- und Zielbereich).

6-Tupel: $\;\; (1,1,0,0,1,0)$.

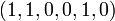Zusammenhang mit anderen Begriffen

In der Literatur werden n-Tupel auch allgemeiner als Familien mit endlichen Indexmengen definiert:^[3]

$(a_1,a_2,...,a_n) := (a_i)_{i \in \{1,2,...,n\}}$

und auch ein 0-Tupel bzw. leeres Tupel lässt sich dann definieren:

$(\,) := (a_i)_{i \in \{\}} = \{\,\}.$

Dies ist möglich, weil jedem n-Tupel, das gemäß der formalen Definition mit geordneten Paaren definiert ist, genau eine entsprechende Familie mit der Indexmenge {1,2,...,n} zugeordnet werden kann. Bezüglich des Gleichheitsaxioms für geordnete Paare sind n-Tupel daher nicht von den zugehörigen Familien zu unterscheiden, ein n-Tupel ist jedoch eine andere Menge als die zugehörige Familie und bei der Definition von Tupeln als Familien wird z. B. das Kartesische Produkt im Gegensatz zur oben genannten Definition assoziativ.

Ebenso allgemeine n-Tupel erhält man aber auch, wenn die oben genannte Definition beibehalten wird, jedoch ein geordnetes Paar allgemeiner als Klasse aller entsprechenden Mengen, die das Gleichheitsaxiom für geordnete Paare erfüllen, oder abstrakt einfach direkt über das Gleichheitsaxiom für geordnete Paare definiert wird.

Einzelnachweise

1. ↑ Randall Holmes: Elementary Set Theory with a Universal Set. Academia-Bruylant 1998. Chapter 4.
2. ↑ N. Bourbaki: Elements of Mathematics: Theory of Sets. §2. H.-D. Ebbinghaus: Einführung in die Mengenlehre. S. 48.
3. ↑ Encyclopaedia of Mathematics: Tuple

Literatur

• Nicolas Bourbaki: Elements of Mathematics: Theory of Sets. Hermann, Paris / Addison-Wesley Reading, Massachusetts, 1968.
• H.-D. Ebbinghaus: Einführung in die Mengenlehre, 4. Aufl., Spektrum Akademischer Verlag, Heidelberg-Berlin 2003.
• Roger Godement: Algebra. Hermann, Paris 1968. §2.