- Quotientenmenge
-
In der Mathematik möchte man in vielen Zusammenhängen Objekte, die sich in gewissen Aspekten ähneln, als gleichwertig ansehen. Eine Formalisierung der Mindestanforderungen an einen solchen Gleichwertigkeitsbegriff ist der Begriff der Äquivalenzrelation.
Beispielsweise ist jeder Begriff, der als die Gleichheit gewisser Eigenschaften definiert werden kann, eine Äquivalenzrelation:
- die Gleichmächtigkeit endlicher Mengen: zwei endliche Mengen heißen gleichmächtig, wenn sie dieselbe Anzahl von Elementen haben;
- die Kongruenz in der Geometrie: zwei Dreiecke sind kongruent, wenn sie dieselben Seitenlängen haben;
- die Ähnlichkeit in der Geometrie: zwei Dreiecke sind ähnlich, wenn sie dieselben Innenwinkel haben;
- die Kongruenz in der elementaren Zahlentheorie: zwei ganze Zahlen heißen kongruent modulo 5, wenn sie bei ganzzahliger Division durch 5 denselben Rest lassen;
- die Gleichheit selbst.
Oft entstehen derartige Begriffe auch aus der Existenz von Abbildungen oder anderen Verbindungen mit gewissen Eigenschaften:
- zwei endliche Mengen sind gleichmächtig, wenn es eine bijektive Abbildung zwischen ihnen gibt;
- zwei Dreiecke sind kongruent, wenn sie durch eine Kongruenzabbildung auseinander hervorgehen;
- zwei Dreiecke sind ähnlich, wenn sie durch eine Ähnlichkeitsabbildung auseinander hervorgehen;
- zwei ganze Zahlen sind kongruent modulo 5, wenn sie durch Addition eines ganzzahligen Vielfachen von 5 auseinander hervorgehen.
Das Wort „äquivalent“ stehe im Folgenden für eine dieser Beziehungen zwischen zwei Objekten; dass zwei Objekte a und b äquivalent sind, sei durch
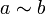 symbolisiert.
symbolisiert.Alle diese Begriffe haben die folgenden drei Eigenschaften:
-
- Jedes Objekt ist zu sich selbst äquivalent.
-
- Wenn a zu b äquivalent ist, dann ist auch b äquivalent zu a (und umgekehrt).
-
- Wenn a zu b äquivalent und b zu c äquivalent ist, dann ist a äquivalent zu c.
Jede Beziehung zwischen Objekten, die diese Eigenschaften hat, heißt eine Äquivalenzrelation.
Die Äquivalenzklasse eines Objektes a ist die Klasse der Objekte, die äquivalent zu a sind.
Im Zusammenhang mit Äquivalenzrelationen gibt es drei verschiedene Sichtweisen:
- einzelne Objekte: Sind zwei Objekte äquivalent oder nicht?
- einzelne Äquivalenzklassen: Wie sieht die Gesamtheit der Objekte aus, die äquivalent zu einem vorgegebenen Objekt sind?
- die Menge der Äquivalenzklassen: Wie sieht die Gesamtheit aller Objekte aus, wenn man äquivalente Objekte als gleich ansieht?
Inhaltsverzeichnis
Anschauliches Beispiel
Ein Beispiel aus der Landwirtschaft soll die eingeführten Begriffe vorweg verdeutlichen. Betrachten wir die Menge aller Nutztiere in einem landwirtschaftlichen Betrieb. Wir definieren nun eine Relation: Wir sagen, zwei Tiere stehen in Relation zueinander, wenn sie von derselben Art sind. Die Kuh Kathrin zum Beispiel steht mit dem Ochsen Otto in Relation, aber nicht mit dem Huhn Heidi. Diese Relation ist eine Äquivalenzrelation: Jedes Tier ist von derselben Art wie es selbst (= „reflexiv“). Ist ein Tier von derselben Art wie das andere, dann ist das andere auch von derselben Art wie das eine (= „symmetrisch“). Wenn Kathrin und Lisa von derselben Art sind und Lisa und Otto von derselben Art, dann sind Kathrin und Otto von derselben Art (= „transitiv“) – alle drei sind Rinder. Eine Äquivalenzklasse besteht hier also aus den Tieren einer Art. Zum Beispiel bilden Hühner eine Äquivalenzklasse und die Rinder eine andere Äquivalenzklasse.
Formale Definition einer Äquivalenzrelation
Eine Relation auf einer Menge M kann mit der Menge der in dieser Relation stehenden Paare identifiziert werden. Danach ist eine Relation auf M einfach eine Menge solcher Paare, d. h. eine Teilmenge der kartesischen Produkte von M mit sich selbst.
Eine Äquivalenzrelation auf einer Menge M ist eine Teilmenge
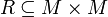 , welche folgende Bedingungen erfüllt:
, welche folgende Bedingungen erfüllt:- Reflexivität: Für alle
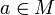 ist
ist 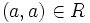 .
. - Symmetrie: Für alle
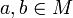 , für die
, für die 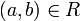 gilt, ist auch
gilt, ist auch 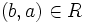 .
. - Transitivität: Für alle
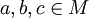 mit
mit 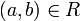 und
und 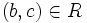 gilt, dass auch
gilt, dass auch 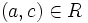 .
.
Üblicherweise schreibt man
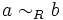 oder einfach
oder einfach 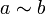 statt
statt 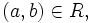
und dann nehmen diese Forderungen genau die in der Einleitung genannte Form an.
Äquivalenzklassen
Ist R eine Äquivalenzrelation auf einer Menge M, so nennt man für ein
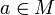 die Teilmenge
die Teilmengedie R-Äquivalenzklasse von a. Ist aus dem Kontext klar, dass Äquivalenzklassen bezüglich R gebildet werden, lässt man den Zusatz „R-“ weg. Andere Schreibweisen sind
Elemente einer Äquivalenzklasse werden ihre Vertreter oder Repräsentanten genannt.
Jedes Element von M ist in genau einer Äquivalenzklasse enthalten. Die Äquivalenzklassen zu zwei Elementen sind entweder gleich oder disjunkt, ersteres genau dann, wenn die Elemente äquivalent sind:
Die Äquivalenzklassen bilden eine Partition von M.
Die Menge der Äquivalenzklassen, der Index
Die Menge der Äquivalenzklassen (manchmal auch Faktormenge oder Quotientenmenge genannt) ist
In dieser Menge werden die Äquivalenzklassen nun nicht mehr als Untermengen von M, sondern als selbstständige Elemente betrachtet. Die Menge der Äquivalenzklassen entsteht, wenn man äquivalente Elemente „gleich macht“. Sie formalisiert (mathematisch) den kognitiven Prozess der Identifizierungsabstraktion.
Die Kardinalität
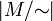 wird manchmal auch als der Index der Äquivalenzrelation R bezeichnet. (Ein Spezialfall ist der Index einer Untergruppe.)
wird manchmal auch als der Index der Äquivalenzrelation R bezeichnet. (Ein Spezialfall ist der Index einer Untergruppe.)Es gibt eine kanonische surjektive Abbildung
die jedem Element seine Äquivalenzklasse zuordnet. Sie ist nur injektiv, wenn die Äquivalenzrelation die Identität ist.
Beispiele
- Schulklassen: die zugrundeliegende Menge M ist die Menge aller Schüler auf einer Schule; zwei Schüler seien äquivalent, wenn sie in dieselbe Klasse gehen.
-
- Äquivalenzklasse eines Schülers ist die Menge aller seiner Mitschüler der gleichen Schulklasse. (Ihn selbst mit eingeschlossen → Reflexivität)
- Die Menge der Äquivalenzklassen ist die Menge der Schulklassen.
- Gleichheit: auf einer beliebigen Menge M seien zwei Elemente äquivalent, wenn sie gleich sind:
-
- Äquivalenzklasse eines Elementes m ist die einelementige Menge {m}.
- Die Menge der Äquivalenzklassen ist die Menge der einelementigen Teilmengen von M; die Abbildung
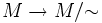 ist eine Bijektion.
ist eine Bijektion.
- Kongruenz in der Zahlentheorie: Die zugrundeliegende Menge ist die Menge Z der ganzen Zahlen, zwei Zahlen sind äquivalent, wenn sie denselben Rest bei Division durch 5 haben. Eine gleichwertige Formulierung ist: wenn ihre Differenz durch 5 teilbar ist.
-
- Äquivalenzklasse einer ganzen Zahl k ist die so genannte Restklasse
- Die Menge der Äquivalenzklassen ist der Restklassenring
- Brüche: Es sei
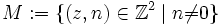 die Menge der Paare ganzer Zahlen, deren zweiter Eintrag von Null verschieden ist. Zwei Paare (z1,n1) und (z2,n2) sollen äquivalent heißen, wenn gilt:
die Menge der Paare ganzer Zahlen, deren zweiter Eintrag von Null verschieden ist. Zwei Paare (z1,n1) und (z2,n2) sollen äquivalent heißen, wenn gilt:
-
- Die Äquivalenzklasse eines Paares (z,n) besteht aus allen Paaren (Zähler, Nenner) für Bruchdarstellungen der rationalen Zahl
 .
. - Die Menge der Äquivalenzklassen wird durch
-
- bijektiv auf die Menge der rationalen Zahlen abgebildet. Ein wichtiger Punkt ist hier die Wohldefiniertheit: wenn [(z1,n1)] = [(z2,n2)] gilt, dann ist das Bild nach der obigen Vorschrift
- einerseits
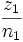 , andererseits
, andererseits 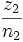 .
.
- einerseits
- Die Äquivalenzrelation war aber gerade so gewählt, dass diese beiden rationalen Zahlen gleich sind.
- Lp-Raum: Auf dem Raum der p-fach integrierbaren Funktionen
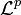 kann eine Äquivalenzrelation wie folgt definiert werden: Seien
kann eine Äquivalenzrelation wie folgt definiert werden: Seien 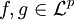 , dann gilt
, dann gilt 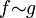 genau dann, wenn f = g bis auf eine Nullmenge gilt. Die Menge aller Äquivalenzklassen bezeichnet man als Lp-Raum. Es gilt also
genau dann, wenn f = g bis auf eine Nullmenge gilt. Die Menge aller Äquivalenzklassen bezeichnet man als Lp-Raum. Es gilt also 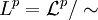 .
.
Universelle Eigenschaft
Ist M eine Menge, R eine Äquivalenzrelation auf M und N eine weitere Menge, so vermittelt die Abbildung
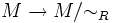 eine Bijektion zwischen folgenden Mengen:
eine Bijektion zwischen folgenden Mengen:- Abbildungen
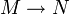 , bei denen R-äquivalente Elemente dasselbe Bild haben
, bei denen R-äquivalente Elemente dasselbe Bild haben
und
- Abbildungen
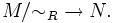
Weitere Äquivalenzbegriffe
Besondere Bedeutung kommt Äquivalenzrelationen zu, die mit einer algebraischen Struktur auf einer Menge kompatibel sind; das Hauptinteresse gilt hier der Menge der Äquivalenzklassen, die die algebraische Struktur „erbt“:
- Faktorraum (für Vektorräume)
- Faktorgruppe (für Gruppen)
- Faktorring (für Ringe)
- Kongruenzrelation (für allgemeine algebraische Strukturen)
Die folgenden Äquivalenzbegriffe entstehen aus der Forderung, dass ein Paar von Abbildungen mit gewissen Eigenschaften zwischen zwei Objekten existiert, die „mehr oder weniger“ invers zueinander sind:
Weitere Beispiele für Äquivalenzrelationen:
- Vervollständigung durch Äquivalenzklassen von Cauchyfolgen
Literatur
- Gerd Fischer: Lineare Algebra. Vieweg-Verlag, ISBN 3-528-03217-0.
- Albrecht Beutelspacher, Lineare Algebra Vieweg-Verlag, ISBN 3-528-56508-X
Wikimedia Foundation.

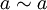
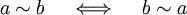
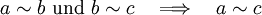
![[a]_R = \{x\in M\mid x\sim_R a\} \subseteq M](/pictures/dewiki/57/98f41bff702f5a8afdbbf95f7957f818.png)
![[a],\quad[a]_\sim,\quad\bar a,\quad a/R,\quad a/{\sim_R}.](/pictures/dewiki/48/080a7e28baa1c40ea800da3874eb6f72.png)
![[a]=[b]\quad\iff\quad a\sim b\quad\iff\quad a\in[b]\quad\iff\quad b\in[a].](/pictures/dewiki/100/d855e5f1e53592daa4c4a9e130ca9449.png)
![M/{\sim} := \{[a] \mid a \in M\}.](/pictures/dewiki/55/79c589453d766f62bd857dd4052ee56e.png)
![M\to M/{\sim},\quad m\mapsto[m],](/pictures/dewiki/100/db4113895f236194517faf8aa02dcb59.png)

![[k] = \bar k=k+5\mathbb Z=\{k+5z\mid z\in\mathbb Z\}=\{\ldots,k-10,k-5,k,k+5,k+10,\ldots\}.](/pictures/dewiki/50/22b3931e2a09c713cab4c789994e1600.png)
![\mathbb Z/5\mathbb Z = \mathbb Z/_{(5)} =\{\bar0,\bar1,\bar2,\bar3,\bar4\} = \{[0], [1], [2], [3], [4]\}.](/pictures/dewiki/55/7f90f3eb7dde603589c5b5761fe825b3.png)
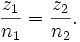
![M/{\sim}\to\mathbb Q,\quad [(z,n)]\mapsto\frac zn](/pictures/dewiki/54/6cd4baf8aed23ef8886e38d5f3d6e508.png)