Radlinie

Eine Zykloide (v. lat. cyclus bzw. griechisch κύκλος kýklos = Kreis und ειδής -eidés = ähnlich) auch zyklische Kurve, Rad- oder Rollkurve ist die Bahn, die ein Kreispunkt beim Abrollen eines Kreises auf einer Leitkurve, zum Beispiel einer Geraden, beschreibt.

Mathematische Darstellung der Zykloiden

Eine Zykloide kann als analytische Gleichung und in Parameterdarstellung dargestellt werden.

Die Parameterdarstellung lautet

$x = r (t - \sin (t)); \quad y = r (1 - \cos (t))$,

wobei r den Radius des Kreises und t den Parameter („Wälzwinkel“) bezeichnet.

Aus dieser lässt sich der Parameter t eliminieren. Die analytische Gleichung lautet

$x(y)= r \arccos \left(\frac{r-y}{r}\right)-\sqrt{y(2r-y)}$.

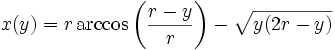Eigenschaften der Zykloide

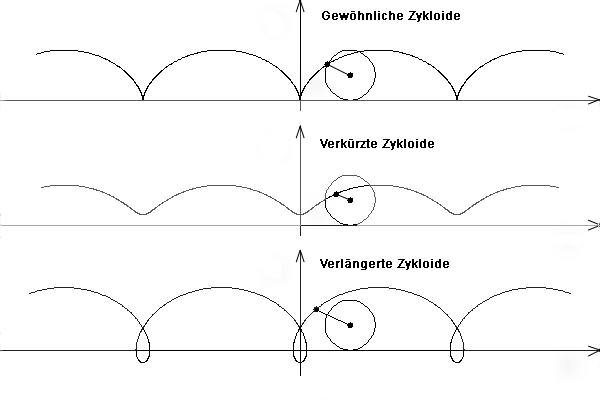
Eine gewöhnliche Zykloide entsteht, wenn ein Kreis auf einer Geraden abrollt. Anschaulich gesprochen bewegt sich ein Punkt auf einem Reifen eines fahrenden Fahrrades (näherungsweise das Ventil) auf einer gewöhnlichen Zykloide. Die Katakaustik, die Evolute und die Evolvente der Zykloide sind selbst wieder Zykloiden. Die Mittelpunkte der Krümmungskreise einer Zykloiden liegen vollständig auf ihrer Evolute.

Eine verkürzte Zykloide entsteht, wenn die Bahn eines Punktes im Inneren des Kreises betrachtet wird, anschaulich etwa der Seitenstrahler beim Fahrrad. Eine verlängerte Zykloide setzt dagegen voraus, dass ein Punkt außerhalb des abrollenden Kreises sich mit dem Kreis mitbewegt. Diese beiden Kurven heißen auch Trochoiden (griechisch τροχός trochos »Rad«).

Beispiele

• Gewöhnliche Zykloiden werden von Punkten auf der Lauffläche eines Autoreifens oder sonstiger Laufräder (Eisenbahn, Seilbahn) und von den Punkten längs der Lauffläche rollender Murmeln beschrieben.
• Verkürzte Zykloiden werden von Punkten mit einem Radius kleiner dem der Lauffläche beschrieben, etwa Punkte von Fahrradspeichen oder die Ansatzpunkte von Pleuelstangen bei einer Dampflokomotive.
• Verlängerte Zykloiden werden von Punkten mit einem Radius größer dem der Lauffläche beschrieben; im Fall von Eisenbahnen wären das alle Punkte des Spurkranzes.

Die Form einer gewöhnlichen Zykloide gleicht einer Aneinanderreihung weiterer Bögen, die verlängerte Zykloide weist an den Spitzen zwischen den Bögen noch Schleifen auf, während bei den verkürzten Zykloiden die Spitzen abgerundet sind.

Eine Brachistochrone beziehungsweise Tautochrone entsteht durch Spiegelung einer Zykloide an der x-Achse.

Die Tautochronie der Zykloide

Tautochronie der Zykloide

Vorausgesetzt, dass Luftwiderstand und Reibung zu vernachlässigen sind, gelangt ein frei beweglicher Massepunkt von jedem Startpunkt auf der Zykloide stets in derselben Zeit an den tiefsten Punkt. Diese Eigenschaft wird auch Tautochronie genannt (Linie gleicher Fallzeit; griechisch ταὐτό tauto dasselbe, χρόνος chronos Zeit).

Epi- und Hypozykloide

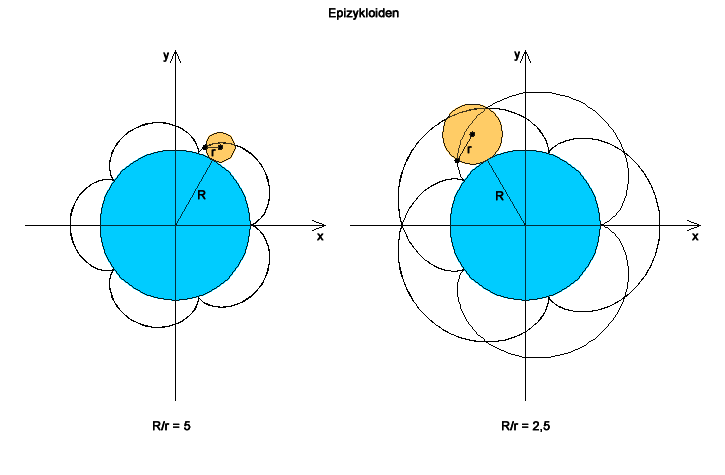
Rollt der Kreis außen auf einem anderen Kreis ab, entstehen Epizykloiden (griechisch ἐπίκυκλος epíkyklos, »Nebenkreis«). Ihr Radius ist gleich der Summe des Radius des Leitkreises und des Durchmessers des bewegten Kreises. Historisch versuchte man die beobachteten Planeten-Bahnen mit teilweise eigentümlich anmutenden Schleifen durch die Epizykeltheorie zu erklären. Rollt ein Kreis um einen feststehenden kleineren Kreis ab, entstehen ebenfalls Epizykloiden. Zur Unterscheidung des Entstehungsmechanismus werden diese Epizykloiden auch Perizykloiden genannt.

Zwei Hypotrochoiden

Zwei Hypotrochoiden (Animation)

Rollt der Kreis dagegen innen in dem anderen Kreis ab, entstehen Hypozykloiden, Kurven mit Spitzen. Wird statt eines Punktes auf dem innereren Kreis ein Punkt außerhalb verwendet und die Strecke von diesem Punkt zur Mitte des inneren Kreises mitgedreht, dann beschreibt dieser Punkt blumig anmutende Kurven, so genannte Hypotrochoiden. Dieser Effekt wird auch als Spielzeug als Spirograph vermarktet in Form von Zahnrädern aus Plastik, die in ihrem Inneren Löcher zum Durchstecken einer Bleistiftspitze enthalten. Die »Leitkurve« wird (in Form einer großen Scheibe mit ausgestanztem Zahnrad im Inneren) auf einem Blatt Papier festgesteckt und danach wird so lange mit dem eingesteckten Stift das abrollende Zahnrad bewegt, bis sich eine geschlossene Kurve ergibt.

Sowohl Epizykloiden als auch Hypozykloiden sind genau dann geschlossene Kurven, wenn sich das Verhältnis der Radien als Bruch aus zwei ganzen Zahlen schreiben lässt, wenn es also rational ist. Bei der technischen Umsetzung in Form von Zahnrädern ist dagegen die Anzahl der Zähne maßgeblich, so dass sich stets geschlossene Kurven ergeben.

Für die Anzahl der „Schleifen“ n von aus einem äußeren Kreis mit dem Radius r_a und einem inneren Kreis mit dem Radius r_i entstehenden Epizykloiden, gilt der Zusammenhang

$n = \frac{\operatorname{max}(r_\mathrm{a},r_\mathrm{i})}{\operatorname{ggT}(r_\mathrm{a},r_\mathrm{i})}$,

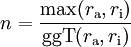für Hypozykloiden verkürzt sich diese Formel auf

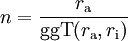$n = \frac{r_\mathrm{a}}{\operatorname{ggT}(r_\mathrm{a},r_\mathrm{i})}$ und liefert die Anzahl der Spitzen.

Gilt r_a = kr_i für natürliches k>1, dann hat die Hypozykloide folglich genau k Spitzen.

• Für k=2 (Cardanische Kreise) ergibt sich eine geradlinige Hypozykloide, deren sämtliche Punkte auf einem Durchmesser liegen.
• Für k=3 ergibt sich eine Deltoide (Hypozykloide mit 3 Spitzen)
• Für k=4 ergibt sich eine Astroide: das »Karo«, wie man es von Spielkarten kennt.

Die Kardioide ist ein Spezialfall der Epizykloide.

Zykloidenverzahnung in der Getriebetechnik

In der Getriebetechnik ist die sogenannte Zykloidenverzahnung eine von mehreren Techniken zur Verzahnung von Zahnrädern und Zahnstangen.

Wichtigste Erkenntnisse seit dem 16. Jahrhundert

Das 17. Jahrhundert, das als „Goldenes Zeitalter der Analysis“ gilt, war auch für die Untersuchung der Zykloide relevant. So beschäftigten sich die besten Mathematiker und Naturwissenschaftler mit dieser besonders ästhetischen Kurve.

Die erste Veröffentlichung zu Zykloiden erfolgte 1570 durch Gerolamo Cardano, der dabei unter anderem die cardanischen Kreise beschreibt. Galileo Galilei unternahm 1598 weitere geometrische Untersuchungen von Zykloiden. Die erste Flächen- und Längenberechnung an einer Zykloide gelang 1629 dem Italiener Bonaventura Cavalieri. Weitere Forschungsanstöße lieferte im gleichen Jahr der Franzose Marin Mersenne.

Weitere Fortschritte durch Quadraturen schafften 1634 Gilles Personne de Roberval und 1635 René Descartes und Pierre de Fermat. Roberval gelang 1638 eine Tangentenkonstruktion, 1641 gelang dies auch Evangelista Torricelli. Torricelli entwickelte bis 1643 eine Quadratur in Beziehung zur Schraubenlinie. Der Engländer Christopher Wren zeigte 1658, dass die Länge einer Zykloide gleich dem Vierfachen des Durchmessers des generierten Kreises ist.

Auf ein Preisausschreiben Newtons aus dem Jahr 1658 hin schaffte Blaise Pascal die Rektifikation, die Quadratur, die Schwerpunktbestimmung und die Kubaturen. Eine Quadratur über eine unendliche Reihe erfolgte 1664 durch Isaac Newton. Gottfried Wilhelm Leibniz entwickelte 1673 die Quadratur über die Quadratrix. Der Niederländer Christiaan Huygens schaffte 1673 die Evolutenbestimmung und Tautochronie.

Durch Leibniz wurde 1686 die Integraldarstellung fertig gestellt. Die letzte wichtigste Erkenntnis war 1697 die Brachistochroneneigenschaft durch Johann Bernoulli.

Siehe auch

• Lissajous-Figur
• Spirograph
• Drehplattentür

Weblinks

• Interaktives Applet zur Erzeugung von Rollkurven
• Die Eigenschaften der Zykloide aus mathematischer, physikalischer und historischer Sicht
• Mathematische Erklärung zu Zykloiden
• Java-Animation zum leichten Verständnis von Zykloiden