Radonmass

Im mathematischen Gebiet der Maßtheorie sind Radonmaße (benannt nach Johann Radon) Maße auf der Borelschen σ-Algebra eines Hausdorff-Raums mit bestimmten Regularitätseigenschaften. Der Begriff wird in der Fachliteratur nicht einheitlich verwendet.

Eine Definition (von Laurent Schwartz ^[1]) lautet:

Ein Radonmaß ist ein Maß auf der Borelschen σ-Algebra eines Hausdorff-Raums, das lokal-endlich und von innen regulär ist.

Beispiele für Maße mit dieser Regularitätseigenschaft sind:

• Die Lebesgue-Stieljes-Maße auf den Borel-Mengen des 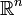$\mathbb R^n$ sind genau die Radonmaße.
• Das Haar-Maß auf lokalkompakten hausdorffschen topologischen Gruppen.

Zu dem Begriff des Radonmaßes kommt man in natürlicher Weise, wenn man positive (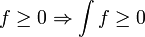$f\ge 0 \Rightarrow \int f \ge 0$) lineare Funktionale „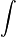$\int$“ (sogenannte Radon-Integrale) auf C_c(X) (den stetigen, reellwertigen Funktionen mit kompaktem Träger) auf einem lokalkompakten Haussdorf-Raum untersucht. In solchen lokalkompakten Räumen ist die Eigenschaft der Lokal-Endlichkeit eines Maßes äquivalent zu Endlichkeit des Maßes auf kompakten Mengen (siehe Borel-Maß).

Einzelnachweise

1. ↑ Laurent Schwartz: Radon measures on arbitrary topological spaces and cylindrical measures. Oxford Universtity Press, London 1973.

Literatur

• Jürgen Elstrodt: Maß- und Integrationstheorie. 4. Auflage, Springer, Berlin 2005, ISBN 3-540-21390-2.