Ausreisser

Ein Ausreißer-Messwert

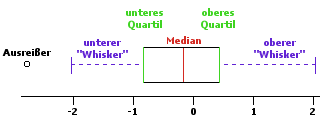Der Boxplot wird über einem Zahlenstrahl dargestellt.

In der Statistik spricht man von einem Ausreißer, wenn ein Messwert oder Befund nicht in eine erwartete Messreihe passt oder allgemein nicht den Erwartungen entspricht. Die „Erwartung“ wird meistens als Streuungsbereich um den Erwartungswert herum definiert, in dem die meisten aller Messwerte zu liegen kommen, z. B. der Quantilabstand Q₇₅ – Q₂₅. Werte außerhalb dieses Intervalls werden (meist willkürlich) als Ausreißer bezeichnet. Im Boxplot werden besonders hohe Ausreißer gesondert dargestellt. Die robuste Statistik beschäftigt sich mit der Ausreißerproblematik.

Überprüfung auf Messfehler

Entscheidend ist es dann, zu überprüfen, ob es sich bei dem Ausreißer tatsächlich um ein verlässliches und echtes Ergebnis handelt, oder ob ein Messfehler vorliegt.

Beispiel: So wurde das Ozonloch über der Antarktis einige Jahre zwar bereits gemessen, die Messwerte aber als offensichtlich falsch gemessen bewertet und in ihrer Tragweite nicht erkannt^[1].

Ausreißertests

Ein anderer Ansatz wurde von u.a. von Ferguson (1961)^[2] vorgeschlagen. Danach geht man davon aus, die Beobachtungen aus einer hypothetischen Verteilung stammen. Ausreisser sind dann Beobachtungen, die nicht aus der hypothetischen Verteilung stammen. Die folgenden Ausreißertests gehen alle davon aus, dass die hypothetische Verteilung eine Normalverteilung ist und prüfen, ob einer oder mehrere der Extremwerte nicht aus der Normalverteilung stammen:

• Ausreißertest nach Grubbs
• Ausreißertest nach Nalimov
• Ausreißertest nach Dixon
• Ausreißertest nach Hampel

Im Rahmen der Zeitreihenanalyse können Zeitreihen, bei denen ein Ausreißer vermutet wird, darauf getestet werden und dann mit einem Ausreißermodell modelliert werden.

Extremwerte vs. Ausreißer

Ein beliebter Ansatz ist es den Boxplot zu nutzen um "Ausreißer" zu identifizieren. Die Beobachtungen ausserhalb der Whisker werden dabei willkürlich als Ausreißer bezeichnet. Für die Normalverteilung kann man leicht ausrechnen, dass knapp 0,7% der Masse der Verteilung ausserhalb der Whiskers liegen. Bereits ab einem Stichprobenumfang von n > 143 würde man daher (im Mittel) mindestens eine Beobachtung ausserhalb der Whiskers erwarten (oder auch k Beobachtungen ausserhalb der Whiskers bei n > 143.3362 * k). Sinnvoller ist es daher zunächst von Extremwerten statt von Ausreißern zu sprechen.

Einzelnachweise

1. ↑ Karl-Heinz Ludwig (2007), Eine kurze Geschichte des Klimas: Von der Entstehung der Erde bis heute (2. Auflage), Beck Verlag, S. 149
2. ↑ Ferguson, T. S. (1961), On the Rejection of outliers, In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, vol. 1, 253-287.

Siehe auch

• M-Schätzer

Weblinks

• Grundlagen der Statistik Ausreißertests
• Learning by Simulations Simulation der Auswirkung eines Ausreißers auf die lineare Regression