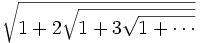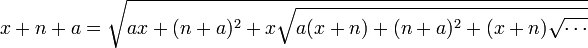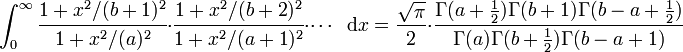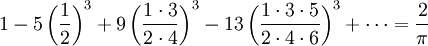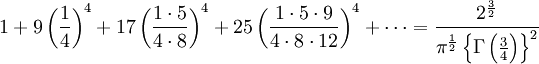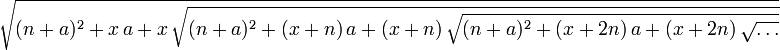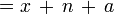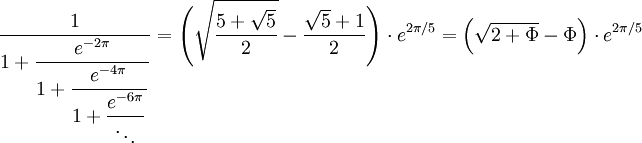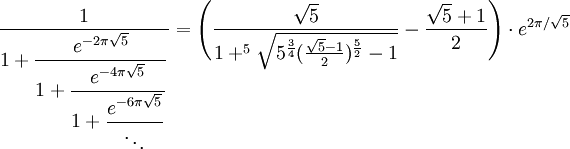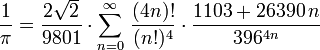Ramanujan

S. Ramanujan

S. Ramanujan [ˈɾɑːmɑːnudʒən] (Srinivasa Ramanujan Aiyangar; FRS); (Tamilisch: ஸ்ரீனிவாஸ ராமானுஜன் ஐயங்கார்); (* 22. Dezember 1887 in Erode, Tamil Nadu; † 26. April 1920 in Kumbakonam, Tamil Nadu) war ein indischer Mathematiker. Er ist vor allem dafür bekannt, sich all sein Wissen autodidaktisch beigebracht zu haben. Von 1914 bis 1919 arbeitete er gemeinsam mit dem britischen Mathematiker Godfrey Harold Hardy am Trinity College der Universität Cambridge in England. Während dieser Zeit wurden ihm zahlreiche Ehrungen und Auszeichnungen zuteil. Ramanujans mathematischer Nachlass tauchte erst 1976 wieder auf und besteht aus über 600 Formeln und Rechensätzen, von denen einige bis heute nicht vollständig bewiesen sind.

Leben

Jugend und Ausbildung

Ramanujan kam 1887 in der tamilischen Stadt Erode zur Welt. Hier lebten seine Großeltern mütterlicherseits. Schon nach kurzer Zeit zog die Familie nach Kumbakonam, wo sie ein kleines Gebäude in der Sarangapani Street bezog. Sein Vater K. Srinivasa Aiyangar arbeitete als Kontorist in einem Sari-Laden, während seine Mutter Komalatammal Srinivasa, die als äußerst gebildete Frau galt, Hausfrau war und in ihrer Freizeit im Chor eines nahen Tempels sang. Die Familie lebte durchgehend in ärmlichen Verhältnissen. Dieser Armut zuträglich waren auch die vielen verschiedenen Umzüge.

Im Sommer des Jahres 1889 gebar Komalatammal einen zweiten Sohn, welcher den Namen Sadagopan erhielt. Das Neugeborene verstarb jedoch bereits weniger als drei Monate darauf. Wenig später, im Dezember desselben Jahres, erkrankte Ramanujan schwer an Pocken, die zu dieser Zeit epidemisch im Distrikt Thanjavur auftrat und tausenden von Personen das Leben kostete. Ramanujan jedoch überlebte. Im Anschluss an diese Krankheit zog er mit seiner Mutter nach Kanchipuram, einer Kleinstadt in der Nähe von Chennai. Hierhin waren zuvor auch seine Großeltern aus Erode gezogen. Im November 1891 wurde ihm durch seine Mutter noch ein Bruder geboren. Dieser überlebte sein erstes Lebensjahr jedoch nicht.

Am 1. Oktober 1892 wurde Ramanujan im Alter von vier Jahren in eine lokale Vorschule eingeschult. Im März 1894 wechselte er auf die Telugu Medium School. Nachdem sein Großvater in Kanchipuram seine Arbeit als Richter verloren hatte, wechselten Ramanujan und seine Mutter erneut den Wohnort und reisten zurück nach Kumbakonam. Dort besuchte der Junge die Kangayan Primary School. Nach dem Tod seines Großvaters väterlicherseits schickte man ihn erneut zu seinen Großeltern mütterlicherseits, die mittlerweile in Chennai lebten. Ramanujan missfiel der Schulbesuch in der Großstadt und er versuchte nach Möglichkeit nicht dorthin zu gehen, doch seine Familie engagierte einen Aufseher, der sicherstellte, dass er nicht schwänzte. Nach sechs Monaten zog Ramanujan zurück zu seinen Eltern nach Kumbakonam. Dort bekam seine Mutter im Jahre 1894 ein weiteres Kind. Doch auch dieses wurde nicht mal ein Jahr alt.

In den folgenden Jahren baute Ramanujan ein sehr enges Verhältnis zu seiner Mutter auf. Sie war zu jener Zeit seine wichtigste Bezugsperson, da der Vater oftmals den ganzen Tag arbeiten musste und nicht zu Hause war. Komalatammal Srinivasa lehrte ihren Sohn die indischen Traditionen, das Kastenwesen sowie die Puranas zu verstehen. Sie brachte ihm religiöse Lieder bei, die sie aus dem Tempel kannte, erklärte ihm die Zelebrierung der Puja und erzog ihn als Brahmane.

Bereits auf der Kangayan Primary School galt Ramanujan als sehr guter Schüler und als er kurz vor seinem zehnten Geburtstag, im November 1897, seine ersten Prüfungen in den Fächern Englisch, Tamil, Geographie und Arithmetik ablegte, war er mit seinen Ergebnissen der beste Schüler des Distriktes. Im darauffolgenden Jahr gebar seine Mutter einen fünften Sohn. Lakshmi Narasimhan, wie er genannt wurde, war gesund und verstarb nicht vorzeitig. Im selben Jahr kam Ramanujan auf die Town High School von Kumbakonam, wo er das erste Mal mit komplizierteren mathematischen Formeln in Kontakt kam. Schon bald bezeichnete man ihn dort als Mathematik-Wunderkind. Mit elf Jahren, also bereits im Jahre 1899, soll er über mehr mathematisches Wissen verfügt haben als zwei College-Studenten, die er aus seiner Nachbarschaft kannte. Man lieh ihm von S. L. Loney verfasste Bücher über fortgeschrittene Trigonometrie aus, welche er in zwei Jahren autodidaktisch durcharbeitete. 1901, mit dreizehn Jahren, beherrschte er den Themenbereich bereits so vollständig, dass er neue Formeln aufstellte, die selbst seine Lehrer in Erstaunen versetzten. Ein Mitschüler aus jener Zeit erinnerte sich gut fünfzig Jahre später:

„Wir verstanden ihn nur selten.“ ^[1]

Seine Klassenkameraden vertraten die Meinung, dass er zwar intelligent sei, man mit ihm aber keine vernünftige Konversation führen konnte. Die restlichen Schüler der Schule jedoch, die ihn nicht so gut kannten, hatten ehrfürchtigen Respekt vor seinen Fähigkeiten. 1902 erhielt Ramanujan seine ersten Zertifikate für besondere Verdienste und Auszeichnungen und half der Schulleitung dabei, die 1.200 Schüler mit ihren jeweils eigenen individuellen Bedürfnissen auf das 35-köpfige Lehrerkollegium zu verteilen. Ramanujan bewältigte Mathematik-Klausuren in der Hälfte der vorgeschriebenen Zeit. Besonders interessiert war er an unendlichen Zahlenreihen. Im Alter von 17 Jahren berechnete Ramanujan die Euler-Mascheroni-Konstante im Kopf auf 15 Stellen hinter dem Komma genau und fand selbstständig die Bernoulli-Zahlen. Anfang des Jahres 1904, Ramanujan war sechzehn Jahre alt, stieß er auf das Buch „A Synopsis of Elementary Results in Pure and Applied Mathematics“ von George Shoobridge Carr. Dieses enthielt über 5.000 mathematische Sätze, welche er sich aneignete. Als er im Jahre 1904 an der High School graduierte, überreichte ihm der Schulleiter Krishnaswami Iyer für seine mathematischen Leistungen den K. Ranganatha Rao prize.

Dieser ermöglichte Ramanujan ein Stipendium am Government College, dem so genannten „Cambridge Südindiens“. Dort konzentrierte er sich jedoch fast ausschließlich auf die Mathematik und vernachlässigte die übrigen Fächer. Aus diesem Grund bestand er die Mehrzahl der Prüfungen nicht und verlor sein Stipendium 1905 wieder.

Daraufhin lief er im August von zu Hause weg und fand in Visakhapatnam Unterkunft. Gegen Ende des Jahres ließ er sich am Pachaiyappa’s College in Chennai als Schüler registrieren. Seine Absicht war, die Prüfungen in einem künstlerischen Fach zu bestehen, um an der University of Madras aufgenommen zu werden. Allerdings fixierte er sich erneut lediglich auf sein Lieblingsfach – in welchem er sich auch exzellent präsentierte – und bestand die Klausuren in vielen anderen Lehrfächern, wie etwa Physiologie, nicht. Dies hatte zur Folge, dass er im Dezember 1906 auch an dieser Schule das Examen nicht erhielt, auch ein weiterer Versuch 1907 war erfolglos. Ramanujan wurde nie Student an einer Universität.

Arbeitsleben in Indien

Ohne höheren Schulabschluss verließ Ramanujan die Lehranstalten und ging unabhängig eigenen mathematischen Untersuchungen nach. Da er jedoch keine Arbeit besaß und somit auch kein regelmäßiges Einkommen bezog, lebte er zu dieser Zeit in extremer Armut am Existenzminimum und litt oftmals Hunger. Am 14. Juli 1909 heiratete er – dem Wunsch seiner Mutter entsprechend – die damals zehnjährige S. Janaki Ammal (1899–1994). Wenige Monate später erkrankte er an einer Hydrozele testis, einer Ansammlung seröser Flüssigkeit in den Hodenhüllen. Diese hätte durch eine kleine Operation behandelt werden können, doch der Familie fehlte das dazu benötigte Geld. Im Januar 1910 erklärte sich ein Arzt jedoch bereit, den Eingriff kostenlos vorzunehmen. Nach der Genesung begab sich Ramanujan auf Arbeitssuche in Chennai und der Umgebung und übernachtete dafür bei Freunden. Er suchte eine Stelle als Kontorist, wie auch sein Vater einer war. Um etwas Geld zu verdienen, gab er zusätzlich einigen Studenten des Presidency College Nachhilfe in Mathematik. Nebenbei beschäftigte er sich weiterhin intensiv mit der Mathematik und veröffentlichte seine Ergebnisse in indischen naturwissenschaftlichen Zeitschriften. Ende des Jahres 1910 erkrankte er erneut schwer. Er fürchtete um sein Leben und bat seinen Freund R. Radakrishna Iyer für den Fall seines Ablebens:

„Wenn ich sterben werde, dann bring bitte diese Bücher zu Professor Singaravelu Mudaliar [vom Pachaiyappa’s College] oder zu dem britischen Professor Edward B. Ross vom Madras College.“ ^[2]

Ramanujan überlebte und reiste in der Folge mit dem Zug von Kumbakonam nach Norden nach Villupuram.

Dort traf er den zuständigen Distrikt-Vorsteher V. Ramaswami Iyer, der kurz zuvor die Indian Mathematical Society (IMS) ins Leben gerufen hatte, und bat um eine Stelle in der Finanzabteilung. Als Bewerbung zeigte er ihm seine Notizbücher mit Formeln. Iyer meinte später:

„Ich war beeindruckt von den außergewöhnlichen Resultaten, die darin [in den Notizbüchern] enthalten waren. Mir kam es nicht in den Sinn, sein Talent durch eine Anstellung auf der untersten Sprosse der Finanzabteilung zu unterdrücken.“ ^[3]

Er schickte Ramanujan mit Empfehlungspapieren zu befreundeten Mathematikern nach Chennai. Diese lasen sich seine Formeln durch und schrieben danach ihrerseits Empfehlungspapiere an R. Ramachandra Rao, den Distrikt-Vorsteher von Nelluru und Sekretär der IMS. Auch Ramachandra Rao zeigte sich beeindruckt von Ramanujans Arbeit, bezweifelte allerdings, dass dieser die Formeln selbst aufgestellt hatte. Gemeinsam mit einigen Bekannten konnte Ramanujan diese Zweifel zerstreuen und rechnete Ramachandra Rao danach Elliptische Integrale, Hypergeometrische Funktionen sowie seine eigene Theorie über die Divergenz unendlicher Reihen vor. Letztere war laut Ramachandra Raos eigenen Worten ausschlaggebend dafür, die mathematische Brillanz Ramanujans anzuerkennen. Dieser bat um Arbeit und finanzielle Unterstützung und Ramachandra Rao schickte ihn zurück nach Chennai. Dort führte Ramanujan mit der finanziellen Hilfe Ramachandra Raos seine mathematischen Arbeiten fort und veröffentlichte einzelne Ergebnisse in der Zeitschrift der IMS.

Eines der ersten Probleme, die er in dem Heft behandelte, war die Berechnung des Ausdrucks

$\sqrt{1+2\sqrt{1+3 \sqrt{1+\cdots}}}$

Er wartete lange Zeit auf eine Lösung durch die Leserschaft, war jedoch am Ende gezwungen, die Lösung selber zu präsentieren, da niemand einen Vorschlag eingeschickt hatte. Er nutzte dabei die Identität:

$x+n+a = \sqrt{ax+(n+a)^2 +x\sqrt{a(x+n)+(n+a)^2+(x+n) \sqrt\mathrm{\cdots}}}$

Gemäß dieser Gleichung war die Lösung des Problems 3. Einer seiner ersten Beiträge im Journal der IMS war die siebzehnseitige Abhandlung „Some Properties of Bernoulli’s Numbers“, in welcher er Eigenschaften der Bernoulli-Zahlen beschrieb. Unter anderem zeigte er eine Methode auf, B_n auf der Grundlage anderer Bernoulli-Zahlen durch Rekursionsrelationen auszurechnen.

Anfangs enthielten Ramanujans Texte in den Fachzeitschriften noch einige Fehler, doch schon bald äußerte sich der Herausgeber der Journals der IMS, M. T. Narayana Iyengar, zu seinen Veröffentlichungen folgendermaßen:

„Mr. Ramanujans Methoden waren so knapp und neuartig und seine Präsentation so mangelhaft in Klarheit und Präzision, dass Normale [mathematische Leser], nicht gewöhnt an solch intellektuelle Gymnastik, ihm kaum folgen konnten.“

Im Januar des Jahres 1912 bewarb er sich erfolgreich um eine Arbeitsstelle im Generalbuchhaltungsbüro von Madras, wo er einen Monatslohn von 20 Indischen Rupien erhielt. Aber nach nur ein paar Wochen sah er sich bereits nach einer neuen Arbeit um. Er erfuhr von freien Stellen beim Buchhaltungsbüro des Hafenamtes in Madras und versuchte angenommen zu werden. Sein Bewerbungsbrief hierfür datierte vom 9. Februar und lautete folgendermaßen:

„Sir,

Ich höre, dass es in Ihrem Büro eine vakante Kontorist-Stelle gibt und ich bitte, mich für dieselbe zu bewerben. Ich habe die Immatrikulationprüfung durchlaufen und bis zum F. A. studiert, war aber infolge verschiedener unglücklicher Umstände verhindert, mein Studium fortzusetzen. Dennoch habe ich all meine Zeit der Mathematik und der Entwicklung des Fachs gewidmet. Ich kann sagen, dass ich recht selbstbewusst bin. Ich kann meine Arbeit gerecht machen, wenn ich für die Stelle ernannt werde. Ich bitte deshalb darum zu ersuchen, dass Sie gut genug sind, die Stelle auf mich zu übertragen.“ ^[4]

Der Bewerbung beigefügt war eine Empfehlung des Mathematikprofessors des Presidence College, E. W. Middlemast, der schrieb, Ramanujan sei „ein junger Mann mit ganz außergewöhnlichen Fähigkeiten in Mathematik“. Drei Wochen nach seiner Bewerbung erfuhr Ramanujan am 1. März 1912, dass er angenommen worden war. An seiner neuen Arbeitsstelle verdiente er nun monatlich 30 Rupien. Die Arbeit fiel ihm nicht schwer und er konnte sie leicht und schnell bewältigen, so dass ihm noch Zeit für mathematische Forschung blieb. Sein Vorgesetzter, Sir Francis Spring, und sein Kollege, S. Narayana Iyer, der ebenfalls Mitglied der IMS war, ermutigten ihn, diese weiter voranzutreiben.

Kontakt mit europäischen Mathematikern

Sir Francis Spring, S. Narayana Iyer, R. Ramachandra Rao und E. W. Middlemast versuchten intensiv europäische Mathematiker für Ramanujans Rechnungen und Ergebnisse zu interessieren. Als erster meldete sich M. J. M. Hill vom University College der Universität London. Er meinte, dass Ramanujans Arbeiten Löcher aufweisen würden, und sagte, dass der Inder, obwohl er „einen Sinn für Mathematik und einiges Talent“ besitze, Mängel im didaktischen Hintergrund und an den Grundlagen habe, mit denen sein Werk nicht von besseren Mathematikern akzeptiert werden würde. Zwar verschaffte Hill Ramanujan keinen Studienplatz bei sich, doch er gab ihm genaue und gut gemeinte Ratschläge für seine zukünftige Arbeit.

Während des Jahres 1912 schickte Ramanujan mehrere Briefe an Henry Frederick Baker und Ernest William Hobson, zwei führende englische Mathematiker an der Universität Cambridge. Freunde halfen ihm bei der Formulierung der Schreiben. Die Adressaten schickten seine Unterlagen jedoch lediglich kommentarlos zurück, sodass er beschloss, den zu jener Zeit bekanntesten Mathematiker, Godfrey Harold Hardy, anzuschreiben, welcher ebenfalls in Cambridge am Trinity College lehrte. Sein neun Seiten umfassender Brief vom 16. Januar 1913, der unzählige mathematische Formeln und Lehrsätze enthielt, begann mit den Worten:

„Sehr geehrter Herr,

ich bitte darum mich Ihnen vorstellen zu dürfen als Angestellter der Buchhaltung in der Hafenverwaltung von Madras mit einem Jahreseinkommen von £ 20. Ich bin jetzt 26 Jahre alt. Ich habe keine abgeschlossene Universitätsausbildung, habe aber den üblichen Unterricht absolviert. [...] Ich bitte Sie, die beigelegten Papiere durchzusehen. Da ich arm bin, möchte ich gerne meine Sätze veröffentlichen, falls Sie überzeugt sind, dass sie einen Wert haben.“

Hardy glaubte zunächst an einen Betrug, da er sich nicht vorstellen konnte, dass ein nicht fertig ausgebildeter Mensch zu solchen Rechenleistungen fähig sei und da zudem zu keiner Formel ein Beweis beigefügt war. Zwar kannte er einige der Formeln, doch die meisten „schienen kaum möglich zu glauben“. Eine dieser für Hardy unverständlichen Formeln befand sich am Ende der dritten Seite des Briefes und lautete (gültig für 0<a<b+½):

$\int_0^\infty \cfrac{1+{x}^2/({b+1})^2}{1+{x}^2/({a})^2} \cdot\cfrac{1+{x}^2/({b+2})^2}{1+{x}^2/({a+1})^2}\cdot\cdots\;\;{\rm d}x = \frac{\sqrt \pi}{2} \cdot\frac{\Gamma(a+\frac{1}{2})\Gamma(b+1)\Gamma(b-a+\frac{1}{2})}{\Gamma(a)\Gamma(b+\frac{1}{2})\Gamma(b-a+1)}$

Ebenso fasziniert war der englische Wissenschaftler von jenen Arbeiten Ramanujans, die die unendlichen Reihen zum Thema hatten, wie etwa:

$1 - 5\left(\frac{1}{2}\right)^3 + 9\left(\frac{1\cdot3}{2\cdot4}\right)^3 - 13\left(\frac{1\cdot3\cdot5}{2\cdot4\cdot6}\right)^3 + \cdots = \frac{2}{\pi}$

und

$1 + 9\left(\frac{1}{4}\right)^4 + 17\left(\frac{1\cdot5}{4\cdot8}\right)^4 + 25\left(\frac{1\cdot5\cdot9}{4\cdot8\cdot12}\right)^4 + \cdots = \frac{2^\frac{3}{2}}{\pi^\frac{1}{2}\left \lbrace \Gamma\left(\frac{3}{4}\right)\right \rbrace^2}$

Das erste Resultat war bereits länger bekannt, das zweite jedoch war Hardy völlig neu. Es leitete sich aus einer Klasse der Hypergeometrischen Funktionen ab, welche zuerst von Leonhard Euler und Carl Friedrich Gauß untersucht worden waren. Hardy fand Ramanujans Ansätze jedoch „sehr viel interessanter“ ^[5]. Über die Theoreme auf der letzten Seite des Briefes äußerte er sich wie folgt:

„[...] Es war mir bald klar, dass Ramanujan noch weit allgemeinere Sätze in seinem Besitz haben musste und dass er manches zurückhielt [...] [Einige Formeln] erschlugen mich regelrecht; ich hatte zuvor nichts auch nur im Entferntesten Ähnliches zu Gesicht bekommen. Ein einziger Blick darauf genügte, um zu erkennen, dass nur ein Mathematiker allerhöchsten Ranges sie niedergeschrieben haben konnte. Sie mussten wahr sein, denn wären sie das nicht gewesen, so hätte kein Mensch die Phantasie besessen, sie zu erfinden. Schließlich [...] musste der Verfasser absolut ehrlich sein, denn große Mathematiker sind häufiger als so unglaublich begabte Diebe und Scharlatane.“ ^[6]

Hardy zeigte seinem Freund und Kollegen John Edensor Littlewood den Brief Ramanujans. Auch Littlewood versetzten die Leistungen des Inders in Erstaunen. Nach einer Diskussion der beiden Engländer bemerkte Hardy, dass der Brief und die Formeln „sicher das Bemerkenswerteste [sind], das ich je erhalten habe“ ^[7] und Ramanujan „ein Mathematiker von der höchsten Qualität, ein Mann von sowohl außergewöhnlicher Originalität als auch Kraft“ ^[7] sei. Ein weiterer Kollege Hardys, der in Chennai lehrende Eric Harold Neville, befand mit Blick auf die Theoreme und Formeln:

„Nicht eines hätte bei der weltweit fortschrittlichsten Untersuchung herausgefunden werden können.“ ^[8]

Hardys Rückschreiben erreichte Ramanujan am 8. Februar 1913 in Chennai. In diesem Schreiben drückte der Brite sein Interesse an der Arbeit des Inders aus:

„Ich wünsche mehr [...] und es ist unerlässlich, dass ich Beweise für einige Ihrer Behauptungen sehe.“

Schon in den ersten Februartagen, also bevor Ramanujan den Brief erhalten hatte, kontaktierte Hardy die indischen Behörden, um eine mögliche Reise Ramanujans nach Cambridge vorzubereiten. Nach der Ankunft des Briefes setzte sich Arthur Davies, der Sekretär des Advisory Committee for Indian Students, mit dem Inder in Verbindung, um mit ihm die Überfahrt zu planen. Doch dieser lehnte die Einladung nach Großbritannien ab, da er als orthodoxer Brahmane Angst hatte, er würde die Zugehörigkeit zu seiner Kaste verlieren, wenn er in ein fremdes Land ginge. Auch seine Mutter hatte Bedenken. Stattdessen sendete Ramanujan einen weiteren Brief mit Formeln an Hardy, welchem er die Worte

„Ich habe in Ihnen einen Freund gefunden, der meine Arbeit mit Sympathie betrachtet.“

anfügte. Um Hardy zu unterstützen, besah sich auch der ehemalige Mathematikprofessor von Cambridge, Gilbert Walker, die Formeln und ermunterte Ramanujan anschließend ebenfalls, nach England zu kommen. Auch der indische Mathematiker B. Hanumantha Rao wollte seinen Landsmann zur Reise überreden. Dazu lud er dessen Arbeitskollegen S. Narayana Iyer zu einem Gespräch der Bildungsbehörde/Fachbereich Mathematik ein, um herauszufinden „was wir für S. Ramanujan tun können“. Bei diesem Treffen einigte man sich darauf, Ramanujan ein zweijähriges Forschungs-Stipendium an der University of Madras zu bewilligen. Pro Monat sollte er 75 Rupien erhalten.

Während seiner Zeit an der Universität veröffentlichte Ramanujan nebenbei weiterhin mathematische Probleme und deren Lösungen in der Zeitschrift der IMS. In dieser Zeit erarbeitete er etwa Wege, um bestimmte Integrale leichter lösen zu können. Auch überarbeitete er die Integral-Theorie von Giuliano Frullani aus dem Jahre 1821 und entwickelte Verallgemeinerungen, mit denen man zuvor scheinbar starre Integrale abschätzen konnte.

Godfrey Harold Hardy suchte in seiner Korrespondenz mit Ramanujan nach weiteren Gründen für dessen Weigerung, die Reise anzutreten. Schließlich bat er Eric Harold Neville, Ramanujan zu überzeugen und nach Großbritannien zu geleiten. Neville führte am 1. Januar 1914 ein Gespräch mit dem indischen Mathematiker. Diesen plagten nun keine Zweifel mehr. Neville sagte zu diesem Treffen später:

„Ramanujan brauchte nun keine Umstimmung und die Opposition seiner Eltern war gebrochen.“ ^[8]

Vermutlich hatten Ramanujans Freunde seiner Mutter Komalatammal gut zugeredet und sie überzeugt, der Reise nach Cambridge zuzustimmen. Ausschlaggebend für sie – aber wohl auch für den Mathematiker selber – war ein Traum, den sie wenige Nächte zuvor gehabt hatte und in dem ihr angeblich die Familiengöttin Namagiri erschienen war. Diese habe ihr, so berichtete die Mutter später, gesagt, sie solle nicht länger zwischen ihrem Sohn und der Erfüllung seines Lebensziels stehen.^[8]

Zusammen mit Eric Harold Neville bestieg Ramanujan am 18. März 1914 (andere Quellen nennen den 17. März) im Hafen von Chennai die „SS Nevasa“. Das Schiff legte um 10:00 Uhr morgens ab. Knapp einen Monat später, am 18. April, lief es in London ein, wo Hardy und Littlewood auf Ramanujan warteten und ihn nach Cambridge fuhren. Er fand bei Neville in der Chesterton Road Unterkunft.

Wissenschaftlicher Erfolg in England

In den letzten Tagen des Mai zog Ramanujan in eine eigene Wohnung am Whewell’s Court um. Diese lag nur fünf Gehminuten von Hardys Büro entfernt. Bereits unmittelbar nach seiner Ankunft begann der Inder damit, seine Arbeit wieder aufzunehmen. Zunächst zeigte er Hardy seine Notizbücher. Zwar hatte er dem Engländer in beiden Briefen zusammen etwa 120 Formeln geschickt, doch die Bücher enthielten noch wesentlich mehr Ansätze, Theoreme und Lösungen. Hardy erkannte, dass einige der Rechnungen falsch und andere bereits von anderen Mathematikern entdeckt worden waren, doch die Mehrzahl waren neue Durchbrüche. Diese beeindruckten Littlewood und Hardy tief, und ersterer meinte:

„Ich glaube, dass er mindestens ein Jacobi ist.“^[9]

Auch Hardy zog Parallelen zwischen Ramanujan und Jacobi:

„[Ich] kann ihn nur mit Euler oder Jacobi vergleichen.“ ^[10]

Zwischen Ramanujan und Hardy gab es jedoch gravierende charakterliche und kulturelle Unterschiede. Der Brite war Atheist und sah sich als Anhänger von Beweisen für Theorien sowie einer gewissen Strenge und Striktheit seiner Wissenschaft. Der Inder dagegen war ein tiefreligiöser Mensch, der zudem während seiner Arbeit vorwiegend auf seine Intuition vertraute. Während der gemeinsamen Jahre versuchte Hardy zudem, die Wissens- und Bildungslücken, die Ramanujan in anderen Fachbereichen aufwies, zu verkleinern, ohne dabei jedoch seine mathematische Inspiration zu unterbrechen.

Trinity College (Great Court)

Im März des Jahres 1916 wurde Ramanujan der Bachelor of Arts für Wissenschaft verliehen. Diese Ehrung galt seiner Arbeit über Hochzusammengesetzte Zahlen, die als Abhandlung in der Zeitschrift der London Mathematical Society veröffentlicht wurde. Hardy äußerte sich, dass diese Rechnungen zu den bis dahin ungewöhnlichsten in der Mathematik zählten und dass Ramanujan sie mit außerordentlichem Scharfsinn bewältigte. Am 6. Dezember 1917 wählte man Ramanujan in die London Mathematical Society. Am 18. Februar 1918 wurde er zum Fellow of the Cambridge Philosophical Society ernannt. Drei Tage später erschien sein Name auf der Kandidatenliste für den Titel Fellow of the Royal Society (FRS). Er war von zahlreichen namhaften Mathematikern „für seine Untersuchung von Elliptischen Funktion und der Zahlentheorie“ vorgeschlagen worden. Unter anderem sprachen sich Hardy, Littlewood, Percy Alexander MacMahon, Joseph Larmor, Thomas John I'Anson Bromwich, Seth Barnes Nicholson, Alfred Young, Edmund Taylor Whittaker, Andrew Russell Forsyth und Alfred North Whitehead für ihn aus. Aber auch Hobson und Baker, jene Professoren, die Ramanujan noch fünf Jahre zuvor nicht geantwortet hatten, befürworteten die Kandidatur. Die Auszeichnung erfolgte am 2. Mai. Ramanujan war damit erst der zweite Inder, dem diese Ehre zuteil wurde und einer der jüngsten Fellows. Noch im selben Jahr, am 10. Oktober, erhielt er zusätzlich noch den Titel Fellow of Trinity College Cambridge.

Zwar unterliefen Ramanujan in seinen Intuitionsrechnungen immer wieder, zum Teil nur kleine, Fehler. Diese jedoch ließen ihn nicht unglaubwürdiger erscheinen. Im Gegenteil: Viele Wissenschaftler nahmen an, dass er doch in gewissem Sinne recht hatte – in seiner eigenen, tieferen, Richtigkeit, die sich ihnen nicht erschloss. Selbst Hardy meinte:

„Und doch bin ich nicht sicher, dass in einem gewissen Sinn sein Versagen nicht wunderbarer gewesen ist als alle seine Triumphe.“ ^[11]

Trotz des wissenschaftlichen Erfolges und der Anerkennung durch Kollegen auf allen Kontinenten fühlte sich Ramanujan in Großbritannien nicht wirklich wohl. Auch lernte er nie, sich seinen Arbeitsalltag zu strukturieren. So soll er beispielsweise Berichten zufolge in stark schwankenden Intervallen gearbeitet haben. Mehrere Male habe er 30 Stunden durchgehend am Schreibtisch gesessen und hätte dann für zwanzig Stunden geschlafen. Diese Unregelmäßigkeiten zehrten an seiner Gesundheit. Zudem litt er unter dem ungewohnten rauen Wetter und hatte vermehrt Kreislaufprobleme. Aus Verzweiflung und Heimweh versuchte er sich sogar vor eine Londoner U-Bahn zu stürzen. Passanten konnten ihn jedoch zurückhalten.

Das Werk

Ramanujan beschäftigte sich während der fünf Jahre in England hauptsächlich mit der Zahlentheorie. Dabei ist er durch viele Summenformeln, welche Konstanten wie die Kreiszahl, Primzahlen und Partitionsfunktionen enthalten, berühmt geworden. Zudem erstellte er eine sehr gute Näherungsformel für die Berechnung des Ellipsenumfangs. Bekannt wurde auch seine Kettenbruchentwicklung, welche er noch 1914 veröffentlichte und mit deren Hilfe man bereits nach nur zehn Schritten 88 Stellen von pi errechnen kann. 1985 gelang es Bill Gosper auf diese Weise, π auf 17.000.000 Stellen hinter dem Komma auszurechnen. Insgesamt fand Ramanujan in Cambridge etwa 3.900 mathematische Resultate, in der Mehrzahl Identitäten und Gleichungen, von denen die meisten im Nachhinein bewiesen werden konnten.

In den Jahren der gemeinsamen Arbeit mit Hardy entstanden zahlreiche Werke über hochzusammengesetzte Zahlen, Mock-Theta-Funktionen (Pseudo-Theta-Funktionen) sowie die Vermutung der tau-Funktion, welche 1974 von Pierre Deligne nachgewiesen wurde. Gemeinsam entwickelten sie das Hardy-Ramanujan-Theorem. Dieser Satz liefert die bis heute exakteste Schätzung der Primzahlen. Ebenfalls entdeckte Ramanujan die Gleichungen

$\sqrt{(n+a)^2 + x\,a + x\,\sqrt{(n+a)^2 + (x+n)\,a + (x+n)\,\sqrt{(n+a)^2 + (x+2n)\,a + (x+2n)\,\sqrt{\dots}}}}$
$= x\,+\,n\,+\,a$

$\frac{1}{\displaystyle 1 + \frac{e^{-2\pi}}{\displaystyle 1 + \frac{e^{-4\pi}}{\displaystyle 1 + \frac{e^{-6\pi}}{\ddots}}}} = \Biggl(\sqrt{\frac{5 + \sqrt{5}}{2}} - \frac{\sqrt{5} + 1}{2}\Biggr) \cdot e^{2\pi/5} = \Bigl( \sqrt{2 +\Phi} - \Phi \Bigr)\cdot e^{2\pi/5}$

$\frac{1}{\displaystyle 1 + \frac{e^{-2\pi\sqrt{5}}}{\displaystyle 1 + \frac{e^{-4\pi\sqrt{5}}}{\displaystyle 1 + \frac{e^{-6\pi\sqrt{5}}}{\ddots}}}} = \Biggl(\frac{\sqrt{5}}{1+^5\sqrt{5^\frac{3}{4}(\frac{\sqrt{5}-1}{2})^\frac{5}{2}-1}} - \frac{\sqrt{5} + 1}{2}\Biggr) \cdot e^{2\pi/\sqrt{5}}$

... mit dem goldenen Schnitt Φ

$\frac{1}{\pi} = \frac{2 \sqrt{2}}{9801} \cdot \sum_{n=0}^\infty\,\frac{(4n)!}{(n!)^4} \cdot \frac{1103 + 26390\,n}{396^{4n}}$

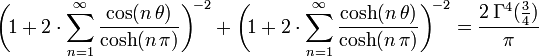$\biggl(\!1 + 2 \cdot \sum_{n=1}^\infty \frac{\cos(n\,\theta)}{\cosh(n\,\pi)}\biggr)^{\!-2} + \biggl(\!1 + 2 \cdot \sum_{n=1}^\infty \frac{\cosh(n\,\theta)}{\cosh(n\,\pi)}\biggr)^{\!-2} = \frac{2\,\Gamma^4(\frac{3}{4})}{\pi}$        für alle θ

Bekannt wurde der Inder unter anderem wegen folgender Entdeckungen:

• Landau-Ramanujan-Konstante (gemeinsam mit dem deutschen Mathematiker Edmund Landau entwickelt)
• Ramanujan-Soldner-Konstante (weiterentwickelte Theorie des deutschen Mathematikers Johann Georg von Soldner)
• Ramanujan-Theta-Funktion
• Rogers-Ramanujan-Identitäten (gemeinsam mit dem britischen Mathematiker Leonard James Rogers entwickelt)
• Ramanujan-Primzahl
• Ramanujans Summe
• Mock Theta Funktion

Krankheit und Tod

Ramanujan hatte zeitlebens gesundheitliche Probleme. Während seines Aufenthalts in England verschlechterte sich sein Zustand aus oben genannten Gründen, aber wohl auch wegen des Mangels an vegetarischer Kost während des Ersten Weltkrieges. So war er bereits zwei Mal an Bakterienruhr erkrankt, als man bei ihm sowohl Tuberkulose als auch Hypovitaminose diagnostizierte. Zur Kurierung dieser Krankheiten wurde er 1918 für kurze Zeit in ein Sanatorium eingewiesen. Ende November desselben Jahres sah Godfrey Harold Hardy jedoch bereits Anzeichen für eine physische Besserung des Gesundheitszustandes Ramanujans und schrieb in einem Brief:

„Ich denke, wir dürfen nun hoffen, dass er sich aus dieser schwierigen Lage befreit hat und auf dem Weg zu einer vollständigen Genesung ist. Seine Körpertemperatur hat aufgehört zu schwanken und er hat fast 6,35 Kilogramm zugenommen. Es hat nie ein Anzeichen für eine Verringerung seines außergewöhnlichen mathematischen Talents gegeben. Er hat selbstverständlich während seiner Krankheit weniger geschafft, aber die Qualität ist gleich geblieben. [...] Er wird mit einem derart bedeutsamen Ansehen und Ruf nach Indien zurückkehren, wie sie noch kein Inder zuvor genossen hat und ich bin zuversichtlich, dass Indien ihn als den Schatz betrachten wird, der er ist. Seine natürliche Unkompliziertheit und Bescheidenheit sind nicht im geringsten vom Erfolg beeinflusst worden – tatsächlich ist alles, was versucht wird, nur dazu da, um ihm zu zeigen, dass er der Erfolg ist.“

Wie im Brief angekündigt, reiste Ramanujan nach dem Ende des Krieges nach Indien zurück. Sein Schiff legte am 27. Februar 1919 in Cambridge ab und erreichte Indien am 13. März. Er hielt sich einige Zeit in Chennai auf, bevor er weiter nach Kumbakonam reiste. Dort starb S. Ramanujan, mittlerweile in Mathematikerkreisen weltbekannt, am 26. April des folgenden Jahres im jungen Alter von nur 32 Jahren an Tuberkulose. Seine Witwe lebte bis zu ihrem Tod 1994 außerhalb von Chennai von einer kargen Rente.

Untersuchungen

Der Arzt D. A. B. Young analysierte und überprüfte 1994 die Krankenakten und medizinischen Unterlagen Ramanujans, in welchen auch die Symptome des Mathematikers niedergeschrieben worden waren, und kam zu dem Schluss, dass als Todesursache anstatt der Tuberkulose vermutlich eine Amöbenruhr anzusehen sei. Er stützte sich zur Untermauerung seiner These auf die Tatsache, dass diese Infektionskrankheit zu jener Zeit stark in Madras grassierte. Zudem war er der Meinung, dass Ramanujans Bakterienruhren nicht vollständig abgeklungen und die Erreger im Körper verblieben waren. So konnte sich die Amöbenruhr später umso schneller entwickeln.

Nachlass, Ehrungen und Nachleben

Ramanujans persönliche Aufzeichnungen waren für einige Jahre verschollen. Seine Witwe gab die vier Notizbücher und einige wenige Manuskripte nach seinem Tod an die University of Madras. Drei Jahre später sendete der dortige Registrar Francis Drewsbury diese zurück an Godfrey Harold Hardy zur Universität von Cambridge. Im Zeitraum zwischen 1934 und 1947 muss dieser die Aufzeichnungen an seinen Kollegen George Neville Watson weitergegeben haben. Nach dessen Tod im Jahre 1965 untersuchte Robert Alexander Rankin seine Unterlagen und schickte die Ramanujan’schen Schriften am 26. Dezember 1968 an die Wren Library des Trinity College.

Dort wurden die Unterlagen, welche in einer Schachtel mit ehemals Watson gehörenden Gegenständen lagen, im Frühling des Jahres 1976 von George E. Andrews wiedergefunden. Die vier Bücher und die Manuskripte enthielten insgesamt knapp 600 von Ramanujan aufgestellte mathematische Formeln. Zu keiner jedoch war ein Beweis beigefügt. Gemeinsam mit Bruce Berndt, einem Mathematiker von der University of Illinois at Urbana-Champaign, bewies Andrews einen großen Teil der Formeln. Die beiden Wissenschaftler fassten ihre Lösungen in einem Buch zusammen. Berndt äußerte sich folgendermaßen über die Entdeckung der Notizbücher:

„Die Entdeckung dieses verlorenen Notizbuches verursachte ungefähr so viel Aufruhr in der mathematischen Welt, wie die Entdeckung von Beethovens zehnter Symphonie in der musischen Welt verursachen würde.“ ^[12]

Am 22. Dezember 1987 (Ramanujans 100. Geburtstag) wurde Ramanujan's Lost Notebook im mit dem Springer-Verlag vernetzten Narosa Publishing House veröffentlicht. Die ersten beiden Exemplare des Buches händigte der damalige indische Premierminister Rajiv Gandhi an S. Janaki Ammal Ramanujan, die Witwe des Mathematikers, und an George E. Andrews aus. Zu einigen Formeln konnten allerdings bis heute keine Beweise gefunden werden und Mathematiker rätseln noch immer über ihre Bedeutung.

Ehrungen

Jahre nach Ramanujans Tod wurde Hardy in einem Gespräch mit dem ungarischen Mathematiker Paul Erdős von diesem gefragt, worin sein größter Beitrag zur Mathematik bestehe. Der Engländer antwortete ohne zu zögern, es handele sich um die Entdeckung Ramanujans; er nannte sie „den einzigen romantischen Vorfall in meinem Leben“. Zusätzlich bemerkte er:

„Man hat mich oft gefragt, ob Ramanujan ein besonderes Geheimnis besessen habe, ob seine Methoden anders als die anderer Mathematiker gewesen seien, ob seine Denkweise nicht eigentlich abnorm gewesen sei. Ich kann diese Frage nicht mit Zuversicht oder Überzeugung beantworten, glaube es aber nicht. Vielmehr glaube ich, dass alle Mathematiker im Grunde in der gleichen Weise denken und dass Ramanujan keine Ausnahme darstellt. Sein Gedächtnis und seine rechnerischen Fähigkeiten waren sehr ungewöhnlich, aber abnorm konnte man sie wohl nicht nennen. Wenn er zwei große Zahlen zu multiplizieren hatte, tat er das auf die übliche Weise; er konnte das mit ungewöhnlicher Geschwindigkeit und Genauigkeit tun, aber nicht schneller und genauer als irgendein Mathematiker, der von Natur aus flink und ans Rechnen gewöhnt ist. Mit seinem Gedächtnis, seiner Geduld und seiner rechnerischen Begabung kombinierte er ein Verallgemeinerungsvermögen, ein Gefühl für Form und eine Fähigkeit, seine Hypothesen rasch zu modifizieren, die oft wirklich verblüffend waren, so dass er in seiner Zeit auf seinem Gebiet ohne Rivalen war. [Sein Werk] hat nicht die Einfachheit und die Zwangsläufigkeit von mathematischer Arbeit höchsten Ranges; wäre es größer, wäre es weniger exotisch. Er hat eine Gabe, die niemand ihm absprechen kann: tiefe und unbesiegbare Originalität. Er wäre vermutlich ein größerer Mathematiker geworden, wäre er in seiner Jugend an die Hand genommen und etwas gezähmt worden: Er hätte mehr Neues entdeckt und ohne Zweifel Wichtigeres. Andererseits wäre er weniger er selbst, Ramanujan, gewesen, sondern eher ein europäischer Professor, und der Verlust wäre vielleicht größer gewesen als der Gewinn.“ ^[11]

Die wichtigsten Auszeichnungen, die Ramanujan entgegennehmen konnte, waren:

• 1904: K. Ranganatha Rao prize for mathematics
• März 1916: Bachelor of Arts für Wissenschaft
• 6. Dezember 1917: Mitglied der London Mathematical Society
• 18. Februar 1918: Fellow of the Cambridge Philosophical Society
• 2. Mai 1918: Fellow of the Royal Society
• 10. Oktober 1918: Fellow of Trinity College Cambridge

Doch auch postum erhielt er diverse Ehrungen. So ließ die indische Regierung im Jahre 1962 eine Briefmarke mit dem Konterfei Ramanujans drucken, um an seinen 75. Geburtstag zu erinnern. Heutzutage ziert der Mathematiker viele verschiedene indische Briefmarken. Im indischen Bundesstaat Tamil Nadu, Ramanujans Heimatstaat, feiert man jedes Jahr am 22. Dezember, seinem Geburtstag, den so genannten State IT Day. Damit soll an die Wurzeln dieses Wissenschaftlers und seine Herkunft aus Tamil Nadu erinnert werden. Das Haus in der Saarangapani Street in Kumbakonam, in dem Ramanujan zusammen mit seiner Familie den größten Teil seiner Kindheit verbracht hat, beherbergt heute ein umfangreiches Museum über den Mathematiker.

Ramanujan als Symbol in der modernen Unterhaltungskultur

Auch die Unterhaltungsindustrie ist mittlerweile auf Ramanujan und sein Werk aufmerksam geworden. So begannen im Jahre 2007 in Tamil Nadu sowie an der Cambridge University die Dreharbeiten zu einem Spielfilm über sein Leben. Der Film wird in indisch-britischer Zusammenarbeit produziert und die Regie übernahmen der Brite Stephen Fry und der Inder Dev Benegal. Von den beiden Produzenten Edward Pressman und Matthew Brown wird derzeit ein weiterer Film zu dem Thema gemacht. Er stützt sich auf das von Robert Kanigel geschriebene Buch Der das Unendliche kannte.

In dem 1997 entstandenen Film „Good Will Hunting“ von Gus van Sant kommt das Verhältnis von Ramanujan und Hardy ebenfalls zur Sprache, weil die Konstellation zwischen Will Hunting (gespielt von Matt Damon) und dem Mathematikprofessor Gerald Lambeau (gespielt von Stellan Skarsgård) ein ähnliches ist.

Auch im Theater war der Mathematiker präsent. So handelte das Drama First Class Man, basierend auf dem gleichnamigen Roman von David Freeman, von Ramanujan und seiner Arbeitsbeziehung zu Godfrey Harold Hardy. Bereits am 21. April 1998 wurde die Oper Ramanujan des deutsch-indischen Komponisten Sandeep Bhagwati über das Leben des Mathematikers im Münchner Prinzregententheater uraufgeführt.^[13]

ICTP Ramanujan Prize

Der ICTP Ramanujan Prize (voller Name: Ramanujan Prize for Young Mathematicians from Developing Countries) ist eine Auszeichnung, die seit 2005 vom Abdus Salam International Centre for Theoretical Physics (ICTP) im Gedenken an den berühmten Inder verliehen wird. Mit dem mit 10.000 US-Dollar dotierten Preis werden junge Mathematiker unter 45 Jahren aus Entwicklungsländern geehrt, die sich auf wissenschaftlichem Gebiet besonders für ihr Land eingesetzt oder um dieses verdient gemacht haben. Der Preisträger wird von einem fünfköpfigen Wissenschaftlerkommitee ermittelt, welches zuvor von der International Mathematical Union (IMU) nominiert wird.

Die Preisträger bisher waren:

• 2005: Marcelo Viana
• 2006: Ramdorai Sujatha
• 2007: Jorge Lauret – „in Anerkennung seiner außerordentlichen Beiträge zur Differentialgeometrie und Darstellungstheorie“

SASTRA Ramanujan Prize

Der SASTRA Ramanujan Prize wird ebenfalls seit 2005 im Gedenken an den berühmten indischen Mathematiker verliehen. Ausgeschrieben ist er von der Shanmugha Arts, Science, Technology & Research Academy (SASTRA) in Ramanujans Heimatdistrikt in Tamil Nadu, dem Thanjavur District. Die Altersgrenze für die Preisverleihung liegt bei 32 Jahren, dem Alter, in dem Ramanujan verstorben war. Wie der ICTP Ramanujan Prize ist auch diese Ehrung mit 10.000 US-Dollar dotiert. Er wird an Mathematiker verliehen, die sich in jenen Bereichen ihrer Wissenschaft hervorgetan haben, die Ramanujan besonders interessierten.

Anekdoten

Es existieren zwei Anekdoten, welche die rechnerischen Leistungen Ramanujans zum Ausdruck bringen. Das erste Beispiel^[14] stammt von Hardy, welcher nach Ramanujans Tod erzählte:

„Ich erinnere mich, dass ich ihn eines Tags besuchen ging, als er in Putney krank im Bett lag. Ich war in Taxi Nr. 1729 gekommen und erwähnte, dass mir diese Zahl ziemlich langweilig vorkäme und ich hoffte, das sei kein ungünstiges Vorzeichen. 'Nein', antwortete er, 'es ist eine sehr interessante Zahl, nämlich die kleinste Zahl, die sich auf zwei verschiedene Arten als Summe zweier Dreierpotenzen darstellen lässt.' Ich fragte ihn natürlich, ob er die Antwort auf das entsprechende Problem für Viererpotenzen wisse, und nach kurzem Nachdenken sagte er, ohne weiteres falle ihm kein Beispiel ein, aber er glaube, die erste derartige Zahl müsste sehr groß sein.“ ^[11]

Sowohl 1³+12³ = 1729 als auch 9³+10³. Die kleinste Zahl, die sich auf zwei verschiedene Arten als Summe zweier Viererpotenzen darstellen lässt, ist tatsächlich sehr groß und lautet 635.318.657. Die entsprechenden Potenzensummen sind 133⁴+134⁴ sowie 59⁴+158⁴.

Die zweite Geschichte^[11] hat Ramanujans Freund aus Cambridge, Prasanta Chandra Mahalanobis, überliefert:

„Ein anderes Mal ging ich auf sein Zimmer, um mit ihm zu Mittag zu essen. Kurz zuvor war der erste Weltkrieg ausgebrochen. Ich hatte ein Exemplar der Monatsschrift Strand Magazine in der Hand, die damals eine Anzahl von Denksportaufgaben zu publizieren pflegte, die der Leser lösen sollte. Ramanujan rührte etwas auf dem Feuer für unsere Mahlzeit. Ich saß nahe am Tisch, blätterte in der Zeitschrift und begann, mich für ein Problem zu interessieren, das eine Beziehung zwischen zwei Zahlen zum Gegenstand hatte. Die Einzelheiten habe ich vergessen, aber ich entsinne mich der Art des Problems. Zwei englische Offiziere waren in Paris in zwei verschiedenen Häusern in einer langen Straße einquartiert. Die Hausnummern standen in einer besonderen Beziehung zueinander; das Problem war, die beiden Zahlen zu finden. Schwierig war es keinesfalls; ich fand die Lösung nach ein paar Minuten des Herumprobierens.

Ich (scherzend): 'Hier ist ein Problem für Sie.'

Er: 'Was für ein Problem?' (Er rührte weiter in seinem Topf.)

Ich las das Problem aus dem Strand Magazine vor.

Er: 'Bitte notieren Sie die Lösung.' (Er diktierte einen Kettenbruch)

Der erste Term war die Lösung, die ich gefunden hatte, jeder weitere Term stellte sukzessive Lösungen für die gleiche Beziehung dar, wenn die Straße unendlich verlängert wurde. Ich war erstaunt.

Ich: 'Kam Ihnen die Lösung blitzartig?'

Er: 'Sobald ich das Problem gehört hatte, war mir klar, dass die Lösung offensichtlich ein Kettenbruch war; dann dachte ich: welcher Kettenbruch? – und die Antwort fiel mir ein. So einfach war das.'“ ^[11]

Zitate

„Eine Gleichung ergibt für mich keinen Sinn, wenn sie nicht einen göttlichen Gedanken zum Ausdruck bringt.“

– S. Ramanujan

„Ist Null geteilt durch Null ebenfalls Eins? Wenn man keine Frucht auf niemand aufteilt, bekommt dann auch jeder eine?“

– Einwurf Ramanujans in der Schule, nachdem der Lehrer erklärt hatte, dass eine Größe durch sich selbst geteilt immer gleich Eins ist.

Literatur

• Godfrey Harold Hardy: Obituary, S. Ramanujan. Nature, 1920
• Godfrey Harold Hardy: Ramanujan – Twelve Lectures on the Subjects Suggested by His Life and Work. Chelsea Publishing Co, 1940, 1978 ISBN 0-8284-0136-5
• Robert Kanigel: Der das Unendliche kannte. vieweg-Verlag, 1995, ISBN 352816509X, deutsche Übersetzung von The Man Who Knew Infinity: a Life of the Genius Ramanujan. New York: Charles Scribner's Sons, 1991. ISBN 0-684-19259-4.
• Eric Harold Neville: Srinivasa Ramanujan. Nature, 1942
• Shiyali Ramamrita Ranganathan: Ramanujan: the Man and the Mathematician. UBS Publishers Distributors, 1967, ISBN 978-8185273372
• P. K. Srinivasan: Ramanujan Memorial Number: Letters and Reminiscences. 1968
• Suresh Ram: Srinivasa Ramanujan. National Book Trust, 1972
• K. Srinivasa Rao: Srinivasa Ramanujan – A Mathematical Genius. East West Books, 1998
• George E. Andrews, Robert Alexander Rankin: Ramanujan: Essays and Surveys. American Mathematical Society, 2001, ISBN 978-0821826249
• Berndt, Bruce C. "An Overview of Ramanujan's Notebooks." in "Charlemagne and His Heritage: 1200 Years of Civilization and Science in Europe" (Hrsg. P. L. Butzer, W. Oberschelp, and H. Th. Jongen), Turnhout, 1998. S.119-146.

Schriften

• mit G. H. Hardy: Une formule asymptotique pour le nombre des partitions de n, Comptes Rendus 164, 1917, S. 35–38
• G. H. Hardy, P. Veṅkatesvara Seshu Aiyar, Bertram Martin Wilson (Hrsg.): Collected papers, Cambridge University Press, 1927
• George E. Andrews, Bruce C. Berndt (Hrsg.): Ramanujan’s Lost Notebook. Springer-Verlag, New York London 2005, ISBN 978-0387255293
• Bruce C. Berndt (Hrsg.): Ramanujan’s Notebooks (fünf Teile), Springer-Verlag, New York
  • Part I, 1985, ISBN 0-387-96110-0
  • Part II, 1999, ISBN 0-387-96794-X
  • Part III, 2004, ISBN 0-387-97503-9
  • Part IV, 1993, ISBN 0-387-94109-6
  • Part V, 2005, ISBN 0-387-94941-0
• George E. Andrews, Robert Alexander Rankin (Hrsg.): Ramanujan – Letters and Commentary. American Mathematical Society, 1995, ISBN 978-0821804704

Einzelnachweise

1. ↑ Kanigel (1995), Seite 24
2. ↑ Kanigel (1995), Seite 67
3. ↑ Srinivasan (1968), Seite 129
4. ↑ Srinivasan (1968), Seite 31
5. ↑ Kanigel (1991), Seite 167
6. ↑ Kanigel (1991), Seite 168
7. ↑ ^{a b} Hardy (1920), Seiten 494 und 495
8. ↑ ^{a b c} Neville (1942), Seite 293
9. ↑ I can believe that he is at least a Jacobi. Brief an Hardy 1913
10. ↑ Godfrey Harold Hardy: Collected Papers of G. H. Hardy. Clarendon Press, 1979, Seite 720
11. ↑ ^{a b c d e} Kurzbiographie Ramanujans auf einer privaten Homepage
12. ↑ „Raiders of the Lost Notebook“ Englischer Text über den Versuch, die Formeln der Notitzbücher zu beweisen
13. ↑ Ulrich Möller-Arnsberg: Die Münchner Biennale 1998. Das Eigene im Fremden – das Fremde im Eigenen, GEMA-Nachrichten 157, Juni 1998
14. ↑ The Hardy-Ramanujan Number

Weblinks

• Website on Srinivasa Ramanujan – von Prof. K. Srinivasa Rao, Chennai, mit zahlreichen Scans der Artikel und Notizbücher, Juni 2002 (englisch)
• Stefan Müller-Stach: Hardy und Ramanujan: Das Taxi mit der Nummer 1729 (PDF-Datei) – Ausstellung vom 6. Juli 2004
• Ein Genie mit Intuition: Ramanujan – Kurzbiographie, Quarks & Co, 5. April 2005
• Ramanujan Prize for Young Mathematicians from Developing Countries – Ramanujan-Preis des ICTP, Triest, Italien
• SASTRA Ramanujan Prize – Ramanujan-Preis der Shanmugha Arts, Science, Technology, Research Academy (SASTRA), Tamil Nadu, Indien

Personendaten
NAME	Ramanujan, S.
ALTERNATIVNAMEN	Srinivasa Ramanujan Aiyangar; Srinivasa Ramanujan Iyengar
KURZBESCHREIBUNG	indischer Mathematiker
GEBURTSDATUM	22. Dezember 1887
GEBURTSORT	Erode, Tamil Nadu
STERBEDATUM	26. April 1920
STERBEORT	Kumbakonam