Reaktions-Diffusionsgleichungen

Reaktionsdiffusionsgleichungen (RD-Gleichungen) beschreiben Vorgänge, bei denen eine lokale Wechselwirkung und zusätzlich eine Diffusion auftritt. Ein Beispiel aus der Chemie sind etwa Modelle für die Belousov-Zhabotinsky-Reaktion, bei der räumliche Muster entstehen, weil eine lokal oszillierende chemische Reaktion mit einem Diffusionsvorgang gekoppelt ist. Ein Beispiel aus der Biologie sind räumliche Ausbreitungsprozesse von Tieren und Pflanzen. Hierbei hat der Interaktionsterm oft die Form einer logistischen Gleichung Kolomogorov-Gleichung. Bei RD-Gleichungen handelt es sich um lineare partielle Differentialgleichungen zweiten Grades, die der Form nach Ratengleichungen sind. Die beschreiben also die zeitliche Änderung einer Größe (z.B. Stoffmenge, Abundanz, Konzentration oä.).

Mathematisch haben sie folgende Form:

$\frac{d}{dt}X=f(X, Y, ...)+ D \cdot \frac{\partial^2}{\partial z^2}X$.

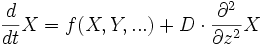Dabei sind X, Y, ... Funktionen der Zeit t und des Ortes z. Sie bilden die Größen ab, deren Dynamik beschrieben wird. Die Funktion f(X, Y, ...) beschreibt den Reaktionsanteil. Der Term 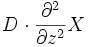$D\cdot\frac{\partial^2}{\partial z^2}X$ stammt aus dem 2. Fickschen Gesetz und beschreibt die Diffusion.

Reaktionsdiffusionsgleichungen finden im Bereich der Chemie in der Technischen Chemie und dem Maschinenbau Anwendung. Dort werden verschiedene Systeme betrachtet, bei denen Konvektion, Diffusion und Reaktion zusammen auftreten (Makrokinetik). Beispiele sind die Auslegung von chemischen Reaktoren oder technische Verbrennungsvorgänge. In der Entwicklungsbiologie spielen Reaktionsdiffusionsgleichungen seit Alan Turing eine überragende Rolle bei der mathematischen Theorie der Morphogenese.

Siehe auch

• Wärmeleitungsgleichung
• Kolmogorov-Gleichung Einfache Reaktionsdiffusionsgleichung mit Sättigungsterm

Literatur

• Dilip Kondepudi, Ilya Prigogine: Modern Thermodynamics. From Heat Engines to Dissipative Structures. John Wiley & Sons, Weinheim, New York 1998
• Murray, J. Mathematical Biology. Springer