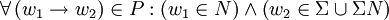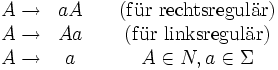Rechtslineare Grammatik

In der theoretischen Informatik werden formale Grammatiken vom Typ 3 der Chomsky-Hierarchie auch reguläre Grammatiken genannt. Die von diesen Grammatiken erzeugbaren Sprachen heißen dementsprechend reguläre Sprachen.^[1]

Definition

Eine reguläre Grammatik 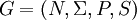$G = \left(N,\Sigma,P,S\right)$ ist eine kontextfreie Grammatik, deren Produktionsregeln weiter eingeschränkt sind. Es gibt rechtsreguläre und linksreguläre Grammatiken, wobei normalerweise mit „regulär“ die rechtsregulären Grammatiken gemeint sind.^[2]

Die rechte Seite einer Produktion w₂ darf für rechtsreguläre Sprachen nur ein Terminalsymbol oder ein Terminal gefolgt von einem Nichtterminal sein. D.h. ein Wort einer solchen regulären Sprache entsteht durch Anfügen von Terminalsymbolen auf der rechten Seite. Entsprechend gilt für linksreguläre Sprachen, dass die rechte Seite w₂ nur ein Terminal oder ein Nichtterminal gefolgt von einem Terminal sein darf.

Für die Produktionen P einer rechtsregulären Grammatik 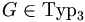$G \in \mbox{Typ}_3$ gilt

$\forall \left(w_1 \rightarrow w_2\right) \in P : \left(w_1 \in N\right) \and \left(w_2 \in \Sigma \cup \Sigma N\right)$

Gültige Produktionen einer regulären Grammatik wären beispielsweise:

$\begin{matrix} A \rightarrow & aA & \quad \mathrm{(f\ddot{u}r \ rechtsregul\ddot{a}r)} \\ A \rightarrow & Aa & \quad \mathrm{(f\ddot{u}r \ linksregul\ddot{a}r)} \\ A \rightarrow & a & \quad A \in N, a \in \Sigma \end{matrix}$

Von G erzeugte Sprache

Die regulären Grammatiken erzeugen die regulären Sprachen. Das heißt jeder regulären Grammatik lässt sich eine reguläre Sprache und umgekehrt zuordnen.

Diese Sprachen sind abgeschlossen unter Komplementbildung, Konkatenation, Schnitt, Vereinigung und Kleenescher Abschluss. Die regulären Sprachen sind die Sprachen, die von einem endlichen Automaten (deterministisch oder nichtdeterministisch) erkannt werden können.

Rechtsreguläre und linksreguläre Grammatiken erzeugen dieselbe Menge von formalen Sprachen, das heißt, zu jeder linksregulären Grammatik gibt es eine rechtsreguläre Grammatik, die dieselbe Sprache erzeugt und umgekehrt.

Quellen

1. ↑ Lutz Engelmann (Hrsg.): Kleiner Leitfaden Informatik und ihre Anwendung. paetec, Berlin 2000, ISBN 3-89517-615-X.
2. ↑ Peter Rechenberg, Gustav Pomberg (Hrsg.): Informatik-Handbuch. Hanser, München/Wien 2006, ISBN 978-3-446-40185-3.