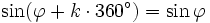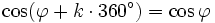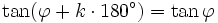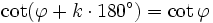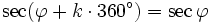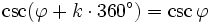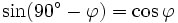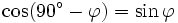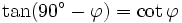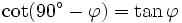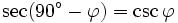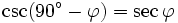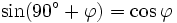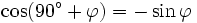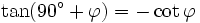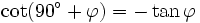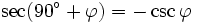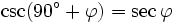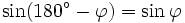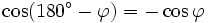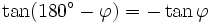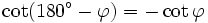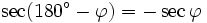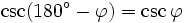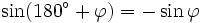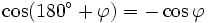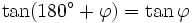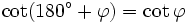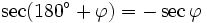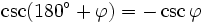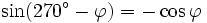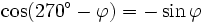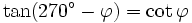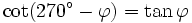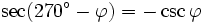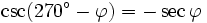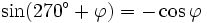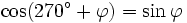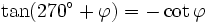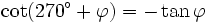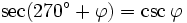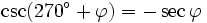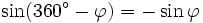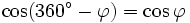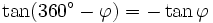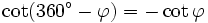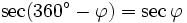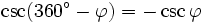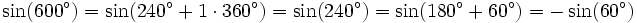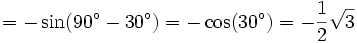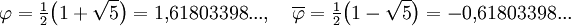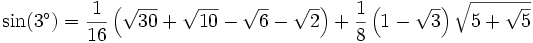Reduktionsformel

Es gibt sicherlich noch andere Reduktionsformeln, hier werden zunächst die der Winkelfunktionen betrachtet.

Reduktionsformeln für Winkelfunktionen

Will man die Werte der Winkelfunktionen Sinus, Kosinus, Tangens, Kotangens, Sekans und Kosekans durch Näherungsformeln oder Tabellen bestimmen, ist es ratsam, das Argument φ möglichst klein zu wählen. Diesem Zweck dienen die folgenden Formeln.

Formeln zur Periodizität

Für alle Winkel $\varphi$ und alle ganzen Zahlen k gilt:

• $\sin(\varphi+k\cdot360^\circ) = \sin\varphi$
• $\cos(\varphi+k\cdot360^\circ) = \cos\varphi$
• $\tan(\varphi+k\cdot180^\circ) = \tan\varphi$
• $\cot(\varphi+k\cdot180^\circ) = \cot\varphi$
• $\sec(\varphi+k\cdot360^\circ) = \sec\varphi$
• $\csc(\varphi+k\cdot360^\circ) = \csc\varphi$

Formeln für 90°-φ (Komplementärformeln)

$\sin(90^\circ-\varphi) = \cos\varphi$

$\cos(90^\circ-\varphi) = \sin\varphi$

$\tan(90^\circ-\varphi) = \cot\varphi$

$\cot(90^\circ-\varphi) = \tan\varphi$

$\sec(90^\circ-\varphi) = \csc\varphi$

$\csc(90^\circ-\varphi) = \sec\varphi$

Formeln für 90°+φ

$\sin(90^\circ+\varphi) = \cos\varphi$

$\cos(90^\circ+\varphi) = -\sin\varphi$

$\tan(90^\circ+\varphi) = -\cot\varphi$

$\cot(90^\circ+\varphi) = -\tan\varphi$

$\sec(90^\circ+\varphi) = -\csc\varphi$

$\csc(90^\circ+\varphi) = \sec\varphi$

Formeln für 180°-φ

$\sin(180^\circ-\varphi) = \sin\varphi$

$\cos(180^\circ-\varphi) = -\cos\varphi$

$\tan(180^\circ-\varphi) = -\tan\varphi$

$\cot(180^\circ-\varphi) = -\cot\varphi$

$\sec(180^\circ-\varphi) = -\sec\varphi$

$\csc(180^\circ-\varphi) = \csc\varphi$

Formeln für 180°+φ

$\sin(180^\circ+\varphi) = -\sin\varphi$

$\cos(180^\circ+\varphi) = -\cos\varphi$

$\tan(180^\circ+\varphi) = \tan\varphi$

$\cot(180^\circ+\varphi) = \cot\varphi$

$\sec(180^\circ+\varphi) = -\sec\varphi$

$\csc(180^\circ+\varphi) = -\csc\varphi$

Formeln für 270°-φ

$\sin(270^\circ-\varphi) = -\cos\varphi$

$\cos(270^\circ-\varphi) = -\sin\varphi$

$\tan(270^\circ-\varphi) = \cot\varphi$

$\cot(270^\circ-\varphi) = \tan\varphi$

$\sec(270^\circ-\varphi) = -\csc\varphi$

$\csc(270^\circ-\varphi) = -\sec\varphi$

Formeln für 270°+φ

$\sin(270^\circ+\varphi) = -\cos\varphi$

$\cos(270^\circ+\varphi) = \sin\varphi$

$\tan(270^\circ+\varphi) = -\cot\varphi$

$\cot(270^\circ+\varphi) = -\tan\varphi$

$\sec(270^\circ+\varphi) = \csc\varphi$

$\csc(270^\circ+\varphi) = -\sec\varphi$

Formeln für 360°-φ

$\sin(360^\circ-\varphi) = -\sin\varphi$

$\cos(360^\circ-\varphi) = \cos\varphi$

$\tan(360^\circ-\varphi) = -\tan\varphi$

$\cot(360^\circ-\varphi) = -\cot\varphi$

$\sec(360^\circ-\varphi) = \sec\varphi$

$\csc(360^\circ-\varphi) = -\csc\varphi$

Anmerkungen

1. Diese Beziehungen werden meist für 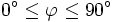$0^\circ \le \varphi \le 90^\circ$ verwendet, sind aber für beliebige Argumente richtig.

2. Um die Formeln im Bogenmaß auszudrücken, muss man jeweils die Gradangaben durch entsprechende Vielfache von π ersetzen, beispielsweise 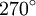$270^\circ$ durch $\frac{3}{2}\pi$.

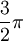Beispiel

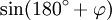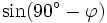Will man sin(600°) berechnen, bringt man zunächst unter Ausnützung der Periodizität den Winkel auf einen Wert zwischen 0° und 360°, nämlich 240°. Anschließend kann man die Formeln für $\sin(180^\circ+\varphi)$ und $\sin(90^\circ-\varphi)$ verwenden.

$\sin(600^\circ) = \sin(240^\circ+1\cdot360^\circ) = \sin(240^\circ) = \sin(180^\circ+60^\circ) = -\sin(60^\circ)$

$= -\sin(90^\circ-30^\circ) = -\cos(30^\circ) = -\frac{1}{2}\sqrt{3}$

Der letzte Wert ergibt sich dabei aus der unten stehenden Tabelle.

Begründung

Geht man von der elementargeometrischen Definition der Winkelfunktionen mit Hilfe des Einheitskreises aus, so lässt sich die Gültigkeit der Formeln für Sinus und Kosinus geometrisch begründen. Kosinus- und Sinuswerte werden dabei als x- und y-Koordinaten von Punkten auf dem Einheitskreis interpretiert. Die Abbildung demonstriert die Reduktionsformeln für die Argumente 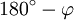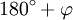$180^\circ-\varphi$, $180^\circ+\varphi$ und $360^\circ-\varphi$. 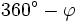Aus der Richtung der Pfeile kann man jeweils das Vorzeichen ablesen.

Auf ähnliche Weise lassen sich die weiteren Sinus- und Kosinus-Formeln bestätigen. Die restlichen Aussagen erhält man dadurch, dass man den Tangens, Kotangens, Secans oder Kosecans eines Winkels durch die entsprechenden Werte der Sinus- und der Kosinus-Funktion ausdrückt.

In der Analysis werden die trigonometrischen Funktionen durch Potenzreihen definiert. Zum Beweis der Reduktionsformeln kann man den Zusammenhang der natürlichen Exponentialfunktion mit der Sinus- und der Kosinus-Funktion heranziehen.

Spezielle Werte der Winkelfunktionen

Funktionswerte für besonders einfache Winkel:

x		sin x	cos x	tan x	cot x	sec x	csc x
0°	0	1/2 √0 = 0	1/2 √4 = 1	0	Polstelle	1	Polstelle
30°	π/6	1/2 √1 = 1/2	1/2 √3	1/3 √3	√3	2/3 √3	2
45°	π/4	1/2 √2	1/2 √2	1	1	√2	√2
60°	π/3	1/2 √3	1/2 √1 = 1/2	√3	1/3 √3	2	2/3 √3
90°	π/2	1/2 √4 = 1	1/2 √0 = 0	Polstelle	0	Polstelle	1

Funktionswerte für weitere Winkel:

x		sin x
15°	π/12	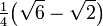$\tfrac14\big(\sqrt6 - \sqrt2\big)$
18°	π/10	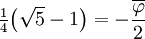$\tfrac14\big(\sqrt5 - 1 \big) =-\frac{\overline{\varphi}}2$
22,5°	π/8	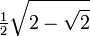$\tfrac12\sqrt{2 - \sqrt2}$
36°	π/5	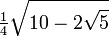$\tfrac14\sqrt{10 - 2\sqrt5}$
54°	3·π/10	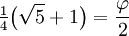$\tfrac14\big(\sqrt5 + 1 \big) =\frac{\varphi}2$
67,5°	3·π/8	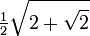$\tfrac12\sqrt{2 + \sqrt2}$
72°	2·π/5	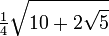$\tfrac14\sqrt{10 + 2 \sqrt5}$
75°	5·π/12	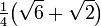$\tfrac14\big(\sqrt6 + \sqrt2 \big)$

Dabei ist $\varphi$ der Goldene Schnitt, und $\overline{\varphi} = 1 - \varphi$:

$\varphi = \tfrac12 \big( 1 + \sqrt5 \big) = 1{,}61803398...,\quad \overline{\varphi} = \tfrac12 \big( 1 - \sqrt5 \big) = -0{,}61803398...$

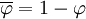Für andere Winkelfunktionen benutze cos(x) = sin(π/2 − x) = sin(90° − x).

Mit Hilfe von Additionstheoremen und Halbwinkelformeln (siehe Trigonometrische Funktion) kann man exakte Werte für weitere Winkel bestimmen. Der kleinste ganzzahlige Winkel für den das möglich ist, beträgt 3° = π/60. Der exakte Wert von sin(3°) ist jedoch ein komplizierter Wurzelausdruck:

$\sin(3^\circ) = \frac{1}{16} \left(\sqrt{30} + \sqrt{10} - \sqrt{6} - \sqrt{2} \right) +\frac{1}{8} \left(1 - \sqrt{3} \right) \sqrt{5 + \sqrt{5}}$