- Regula Falsi
-
Das Regula-Falsi-Verfahren (lat. „Regel des falschen Ansatzes“) ist eine Methode zum numerischen Berechnen von Nullstellen reeller Funktionen. Es kombiniert Methoden vom Sekantenverfahren und der Bisektion.
Inhaltsverzeichnis
Das Verfahren (Primitivform)
Das Regula-falsi-Verfahren startet mit zwei Stellen (in der Nähe der Nullstelle) a0 und b0, deren Funktionsauswertungen f(a0), f(b0) unterschiedliches Vorzeichen haben. In dem Intervall [a,b] befindet sich somit nach dem Zwischenwertsatz (für stetiges f) eine Nullstelle. Nun verkleinert man in mehreren Iterationsschritten das Intervall und bekommt so eine immer genauere Näherung für die Nullstelle.
Iterationsvorschrift
In Schritt k berechnet man
Nun wählt man ak, bk folgendermaßen:
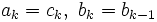 falls
falls 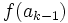 und
und 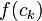 gleiches Vorzeichen haben
gleiches Vorzeichen haben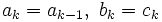 falls
falls 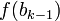 und
und 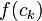 gleiches Vorzeichen haben
gleiches Vorzeichen haben
Bemerkungen
- Die Berechnung des ck entspricht dem Anwenden des Sekantenverfahrens mit einer Iteration im (k − 1)-ten Intervall. Im Gegensatz zum Sekantenverfahren befindet sich in diesem Intervall aber stets eine Nullstelle.
- Geometrisch kann man ck als die Nullstelle der Sekante durch
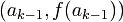 und
und 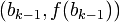 deuten.
deuten. - ck liegt natürlich immer im Intervall
![\left[a_{k-1}, b_{k-1}\right]](/pictures/dewiki/100/dd1bc8e630cbba453a3f7fad7c41a93a.png) .
. - Solange f(x) im k-ten Intervall nicht strikt konkav bzw. konvex ist, also
![\forall\zeta(\zeta\in[a_k,b_k]\rightarrow\exists\xi(\xi\in[a_k,b_k]\rightarrow f''(\zeta)\cdot f''(\xi)\leq 0))](/pictures/dewiki/97/a9da761d2a3c672e9d05857c248e68c2.png) , liegt superlineare Konvergenz vor.
, liegt superlineare Konvergenz vor.
Verbesserung des Verfahrens
Ist f(x) konkav oder konvex im Intervall [ak,bk], also
![\forall\xi(\xi\in[a_k,b_k]\rightarrow\forall\zeta(\zeta\in[a_k,b_k]\rightarrow f''(\xi)\cdot f''(\zeta)>0))](/pictures/dewiki/49/1342a42f30ade0ab52b01fba84ab13da.png) , so bleibt eine der Intervallgrenzen für alle weiteren Iterationen stehen. Die andere konvergiert jetzt nur noch linear gegen die Lösung.
, so bleibt eine der Intervallgrenzen für alle weiteren Iterationen stehen. Die andere konvergiert jetzt nur noch linear gegen die Lösung.Abhilfe schaffen die folgenden Verfahren.
Illinois-,Pegasus- und Anderson/Björk-Verfahren
Den folgenden Algorithmus haben diese Verfahren gemeinsam:
Dabei sind x1,x2 die Intervallgrenzen im k-ten Schritt, f1,f2 und fz die Funktionswerte an den Stellen x1,x2 und z.
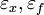 sind die Abbruchgrenzen und m der Verkürzungsfaktor.
sind die Abbruchgrenzen und m der Verkürzungsfaktor. 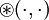 steht hier für eine nicht näher spezifizierte, zweistellige Boolesche Funktion. Sinnvolle Funktionen währen hier die Disjunktion, die Konjunktion, die Negation des ersten und die Negation des zweiten Operanden. Im ersten Fall muss eine der beiden Abbruchgrenzen, im zweiten Fall beide, im dritten Fall lediglich
steht hier für eine nicht näher spezifizierte, zweistellige Boolesche Funktion. Sinnvolle Funktionen währen hier die Disjunktion, die Konjunktion, die Negation des ersten und die Negation des zweiten Operanden. Im ersten Fall muss eine der beiden Abbruchgrenzen, im zweiten Fall beide, im dritten Fall lediglich 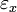 und im vierten Fall
und im vierten Fall 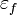 unterschritten werden, damit
unterschritten werden, damit 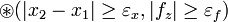 falsch wird und das Verfahren abbricht.
falsch wird und das Verfahren abbricht.Die unterschiedlichen Verfahren unterscheiden sich lediglich im Verkürzungsfaktor m.
- Illinois-Verfahren
- mI = 0.5
- Pegasus-Verfahren
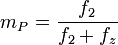
- Anderson/Björk-Verfahren
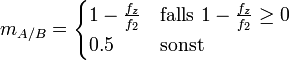
Bemerkungen
- Die Konvergenz der Verfahren ist superlinear und mit der des Sekantenverfahrens vergleichbar.
- Durch die superlineare, garantierte Konvergenz und den relativ geringen Rechenaufwand je Iteration, sind diese Verfahren bei eindimensionalen Problemen i. d. R. anderen Verfahren (wie z. B. dem Newton-Verfahren) vorzuziehen.
Wikimedia Foundation.


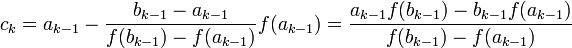
![\!\,
\begin{array}{l}
\text{solange}~\circledast(|x_2-x_1|\geq\varepsilon_x,|f_z|\geq\varepsilon_f):\\
~~\left[
\begin{array}{l}
z:=x_1-\frac{f_1}s~\text{mit}~s=\frac{f_2-f_1}{x_2-x_1}\\
f_z:=f(z)\\
\text{falls}~f_z\cdot f_2<0:\\
~~\left[x_1:=x_2,f_1:=f_2,x_2:=z,f_2:=f_z\right.\\
\text{sonst}:\\
~~\left[f_1:=m\cdot f_1,x_2:=z,f_2:=f_z,x_1~\text{bleibt}\right.\\
\end{array}\right.\\
\text{nimm beliebigen Wert aus}~[x_1,x_2]~\mathrm{als~N\overset{..}{a}herung~f\overset{..}{u}r}~x^*
\end{array}](/pictures/dewiki/57/95b048ffa43f0c1375cb92deb1a8f32b.png)