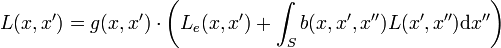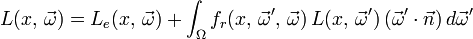Renderinggleichung

Die Rendergleichung, auch Rendering-Gleichung genannt, wird in der 3D-Computergrafik verwendet. Es handelt sich um eine Integralgleichung, die die Energieerhaltung bei der Ausbreitung von Lichtstrahlen beschreibt und somit die mathematische Basis für alle Algorithmen zur globalen Beleuchtung bildet.

Geschichte und Einordnung

Im Prinzip war alles, was zur Berechnung dreidimensionaler Bilder nötig war, schon lange vor der Rendergleichung vorhanden: Die Maxwellschen Gleichungen (1861–1864), die spezielle Relativitätstheorie (1905) und die Quantenmechanik (1920er) erklären die Interaktion von Licht und Materie so exakt, dass mit ihnen theoretisch die Berechnung beliebig realistischer Bilder möglich wäre.

Für die 3D-Computergrafik erwies sich jedoch bereits sehr früh, dass es völlig unpraktikabel ist, mit diesen grundlegenden Modellen zu arbeiten; sie erfordern in den meisten Fällen einen selbst mit heutigen Computern nicht zu bewältigenden Rechenaufwand. Es zeigte sich jedoch auch, dass es nicht nötig war, mit derart exakten Modellen zu arbeiten: Die Quantenmechanik erklärt Effekte im Kleinen, die im menschlichen Alltag nicht wahrnehmbar sind (vgl. etwa Doppelspaltexperiment), die Relativitätstheorie erklärt Sachverhalte im Großen, die hauptsächlich bei astronomischen Größenordnungen ihre Wirkung entfalten (vgl. etwa Raumzeit) und selbst einige Auswirkungen der Maxwellschen Gleichungen (vgl. etwa Interferenz) sind für die Praxis der Computergrafik oft bedeutungslos.

In der Folge arbeiteten die Forscher daher verstärkt mit der geometrischen Optik, die noch auf das antike Griechenland zurückgeht und das Verhalten des Lichts im Großen – also unter Vernachlässigung seiner Welleneigenschaften – beschreibt. So entstanden Ansätze und Techniken, die statt komplexen Wellen einfache Lichtstrahlen durch die Szene verfolgen und in bewältigbarem Zeitaufwand zu passablen Ergebnissen führten, nämlich Raytracing und Radiosity.

In diese Entwicklung hinein veröffentlichte James T. Kajiya 1986 die Rendergleichung. Kajiya zeigte, dass alle bis dato verbreiteten Rendertechniken direkt aus der Rendergleichung hergeleitet werden können. Damit gab es erstmals einen gemeinsamen mathematischen Unterbau, auf dem die Techniken verglichen werden konnten.

Die Rendergleichung führte in der Folge nicht nur zu einer Systematisierung des Wissensgebietes sondern inspirierte auch zahlreiche Weiterentwicklungen. Sie gilt heute als dermaßen fundamental, dass viele fälschlicherweise annehmen, Raytracing sei aus der Rendergleichung entstanden oder die vorher entstandene Radiosity-Gleichung sei als Umformung aus ihr hervorgegangen.

Formel

Ursprüngliche Formel

Die Rendergleichung lautet:

$L(x,x^\prime) = g(x,x^\prime) \cdot \left( L_e(x,x^\prime)+\int_{S} b(x,x^\prime,x^{\prime\prime})L(x^\prime,x^{\prime\prime})\mathrm{d}x^{\prime\prime}\right)$

Sie beschreibt, wie viel Licht einen Oberflächenpunkt x von einem anderen Oberflächenpunkt x' aus erreicht. Dabei wird ein dritter Oberflächenpunkt x'' berücksichtigt, dessen Licht zunächst auf x' trifft und von dort aus nach x reflektiert wird. Die einzelnen Teile haben die folgende Bedeutung:

• Der „Energiefluss“ L(x,x') gibt an, wie viel Licht x von x' aus auf direktem Weg erreicht. Es handelt sich um eine Strahldichte mit der Einheit [W / (m² sr)]. Analoges gilt für den Term L(x',x'').
• Der „geometrische Term“ g(x,x') beschreibt die gegenseitige Lage der Punkte in der Szene. Normalerweise hat der Term den Wert 1/r², wobei r die Entfernung von x und x' ist. Er gibt dann an, wie viel des von x' ausgehenden Lichtes x tatsächlich exakt trifft. Liegt zwischen x und x' eine weitere Oberfläche, so ist der Term jedoch 0, das heißt bei x kommt kein Licht von x' auf direktem Weg an. Dies gilt auch, falls die dazwischen liegende Oberfläche völlig durchsichtig ist; in diesem Fall nimmt die Oberfläche das Licht auf der einen Seite auf und strahlt es auf der anderen Seite neu aus.
• Der „Emissionsterm“ L_e(x,x') gibt an, wie viel Licht von x' aus nach x abgestrahlt wird (falls x' eine Lichtquelle der Szene darstellt). Dies ist wiederum eine Strahldichte mit der Einheit [W / (m² sr)].
• Der „Streuungsterm“ b(x,x',x'') gibt an, welcher Anteil des Lichts, das x' von x'' aus erreicht, in Richtung x reflektiert wird. Es handelt sich hierbei um eine bidirektionale Reflektanzverteilungsfunktion (BRDF).
• S ist die Gesamtheit aller Flächen in der Szene.

Kajiya stellte die Rendergleichung in leicht abgewandelter Form vor, diese Darstellung hat sich inzwischen jedoch als zweckmäßiger erwiesen. In der ursprünglichen Form war der Emissionsterm keine Strahldichte und der Streuungsterm war ein dimensionsloses Konstrukt statt einer BRDF.

Äquivalente Darstellung

Bilder aus Kajiyas Veröffentlichung von 1986. Das Bild links wurde mit normalem Raytracing berechnet, das rechte mit Path Tracing. Durch das Aussenden von Strahlen auf allen Oberflächen werden Lichteffekte wie diese Kaustik möglich.

Äquivalente Darstellungsformen der Rendergleichung werden gewählt, um andere Anwendungsfälle anschaulicher zu beschreiben. Verbreitet ist die folgende Darstellung, die beschreibt, wie viel Licht vom Oberflächenpunkt x aus in Richtung des Vektors 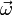$\vec \omega$ abgestrahlt wird:

$L(x, \, \vec \omega) = L_e(x, \, \vec \omega) + \int_{\Omega}{f_r(x, \, \vec \omega^\prime, \, \vec \omega) \, L(x, \, \vec \omega^\prime) \, (\vec \omega^\prime \cdot \vec n) \, d\vec \omega^\prime}$

Die einzelnen Teile haben im wesentlichen dieselbe Bedeutung wie in der anderen Darstellung, sind jedoch in Abhängigkeit von der Richtung statt eines zweiten oder dritten Punktes gegeben:

• Der Energiefluss 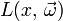$L(x, \, \vec \omega)$ gibt an, wie viel Licht von x aus in Richtung 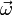$\vec \omega$ abgestrahlt wird; es handelt sich auch hier um die Strahldichte.
• Der Emissionsterm 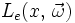$L_e(x, \, \vec \omega)$ gibt an, wie viel Licht von x aus in Richtung 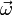$\vec \omega$ ausgestrahlt wird (falls der Punkt selbst eine Lichtquelle darstellt).
• Der Streuungsterm 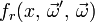$f_r(x, \, \vec \omega^\prime, \, \vec \omega)$ ist eine BRDF mit Einfallswinkel 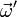$\vec \omega^\prime$ und Reflexionswinkel $\vec \omega$.
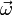• Der Term 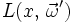$L(x, \, \vec \omega^\prime)$ beschreibt, wie viel Licht aus Richtung 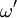$\omega^\prime$ den Punkt x erreicht.
• $\vec n$ ist die Normale der Oberfläche im Punkt x.
• Ω ist die Gesamtheit aller Winkel der Hemisphäre über der Oberfläche.

Die Werte innerhalb des Integrals lassen sich z. B. durch Raytracing, also durch das Aussenden eines Lichtstrahls in Richtung 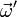$\vec \omega^\prime$, berechnen. Die Annäherung des Integrals durch eine Monte-Carlo-Simulation und das rekursive Aussenden von Lichtstrahlen führt zum Path Tracing, das Kajiya zusammen mit der Rendergleichung beschrieb.

Literatur

• James T. Kajiya: The rendering equation. In: Proceedings of the 13th annual conference on Computer graphics and interactive techniques (SIGGRAPH) 1986, ACM Press, S. 143-150 (PDF)